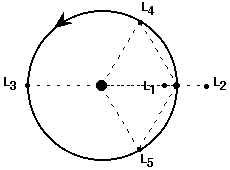
Keringjen m1 és m2 tömegpont a közös tömegközéppont
körül. Ha a harmadik testet az L1,...,L5 Lagrange-pontok valamelyikébe
helyezzük, akkor a három test egymáshoz viszonyított
helyzete, alakzata a mozgás során önmagához hasonló
marad. Az L1, L2, L3 pontok esetén állandóan egy egyenesen
lesznek, az L4 és L5 pont esetén mindig egy szabályos
háromszög csúcsaiban helyezkednek el. A Lagrange-pontok
helyét, koordinátáit az m1 és m2 tömegek
aránya határozza meg.
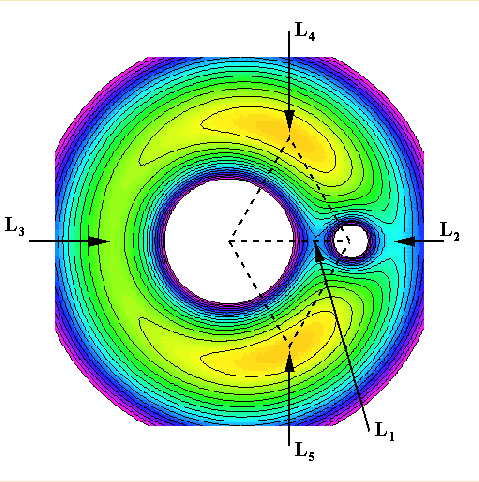
A gravitációs potenciál két tömegpont
körül (felülnézeti metszet). Ezeket az ekvipotenciális
felületeket zéró sebességű felületeknek
is nevezzük, illetve a kettőscsillagok esetében Roche-felületeknek.
A felületeket az W(x,y)=C adja, ahol
C a Jacobi konstans. C=3 (minimális) az L4 és L5 pontokban.
3=C4=C5<=C3<=C2<=C1<=4,25.
A harmadik testre vonatkozó C értéke meghatározza,
hogy a test hol mozoghat.
Stabilitás: vajon az ezen pontokból kissé kimozdított
harmadik test visszatér-e oda vagy eltávozik? Az L1, L2,
L3 pontok nem stabilak (csak átmenetileg, kb. 1 hónapig,
a körülöttük kis ellipszisen, retrográd keringő
testek számára), az L4, L5 pontok is csak akkor stabilak,
ha az m2/m1 tömegarány kisebb mint 0,04.
Gyakorlati alkalmazások:
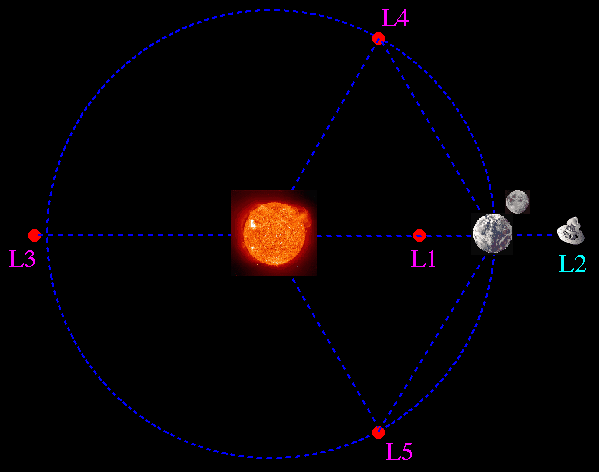
Lagrange-pontok a Nap-Föld rendszerben (nem méretarányos
ábra!).
A tőlünk 1,5 millió km-re lévő L2 pontban a MAP
űrtávcső kis rajza látható.
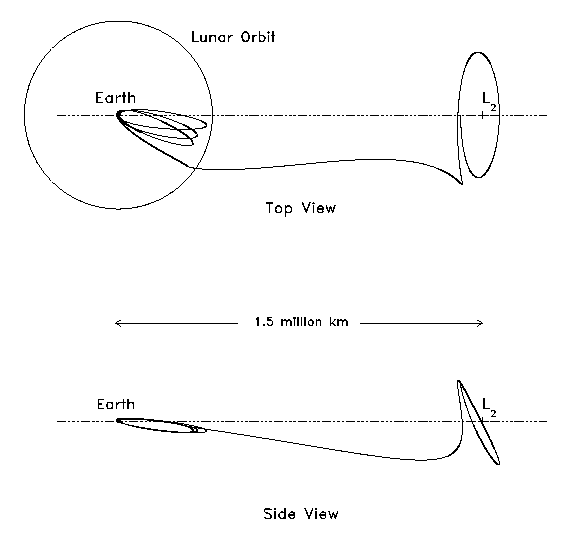
A MAP L2 pontba juttatásának pályája (2000-ben?).
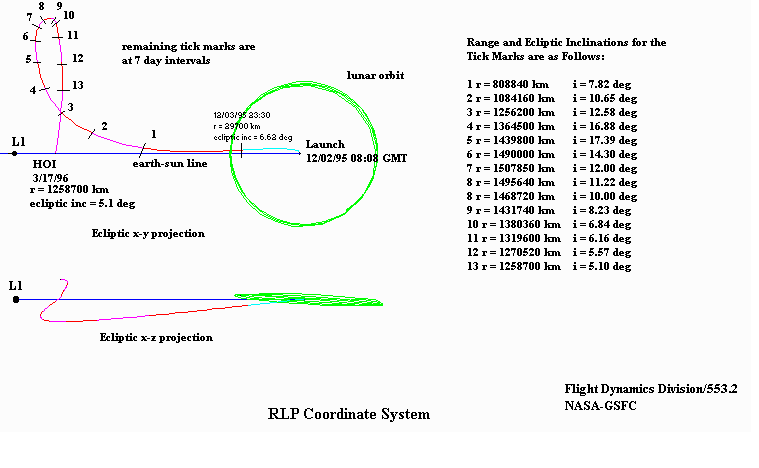
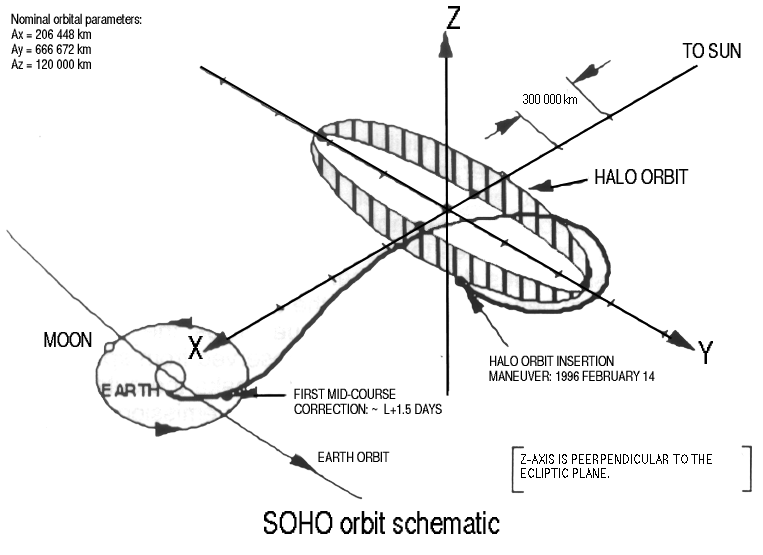
A SOHO napkutató
űrtávcső pozíciója és az L1 pontba
juttatása.
The L1 point of the Earth-Sun system affords an uninterrupted view of the sun and is currently home to the Solar and Heliospheric Observatory Satellite SOHO. The L2 point of the Earth-Sun system will soon be home to the MAP Satellite and (perhaps) the Next Generation Space Telescope. The L1 and L2 points are unstable on a time scale of approximately 23 days, which requiress satellites parked at these positions to undergo regular course and attitude corrections.
NASA is unlikely to find any use for the L3 point since it remains hidden behind the Sun at all times. The idea of a hidden "Planet-X" at the L3 point has been a popular topic in science fiction writing. The instability of Planet X's orbit (on a timescale of 150 days) didn't stop Hollywood from turning out classics like The Man from Planet X.
The L4 and L5 points are home to stable orbits so long as the mass ratio between
the two large masses exceeds 24.96. This condition is satisfied for both the
Earth-Sun and Earth-Moon systems, and for many other pairs of bodies in the
solar system. Objects found orbiting at the L4 and L5 points are often called
Trojans after the three large asteroids Agamemnon, Achilles and Hector that
orbit in the L4 and L5 points of the Jupiter-Sun system. (According to Homer,
Hector was the Trojan champion slain by Achilles during King Agamemnon's siege
of Troy). There are hundreds of Trojan
Asteroids in the solar system. Most orbit with Jupiter, but others orbit
with Mars. In addition, several of Saturn's moons have Trojan companions. No
large asteroids have been found at the Trojan points of the Earth-Moon or Earth-Sun
systems. However, in 1956 the Polish astronomer Kordylewski discovered large
concentrations of dust at the Trojan points of the Earth-Moon system. Recently,
the DIRBE instrument on the COBE
satellite confirmed earlier IRAS observations of a dust
ring following the Earth's orbit around the Sun. The existence of this ring
is closely related to the Trojan points, but the story is complicated by the
effects of radiation pressure on the dust grains.
A part of this page was written by Neil
J. Cornish.
