Fedési kettőscsillagok

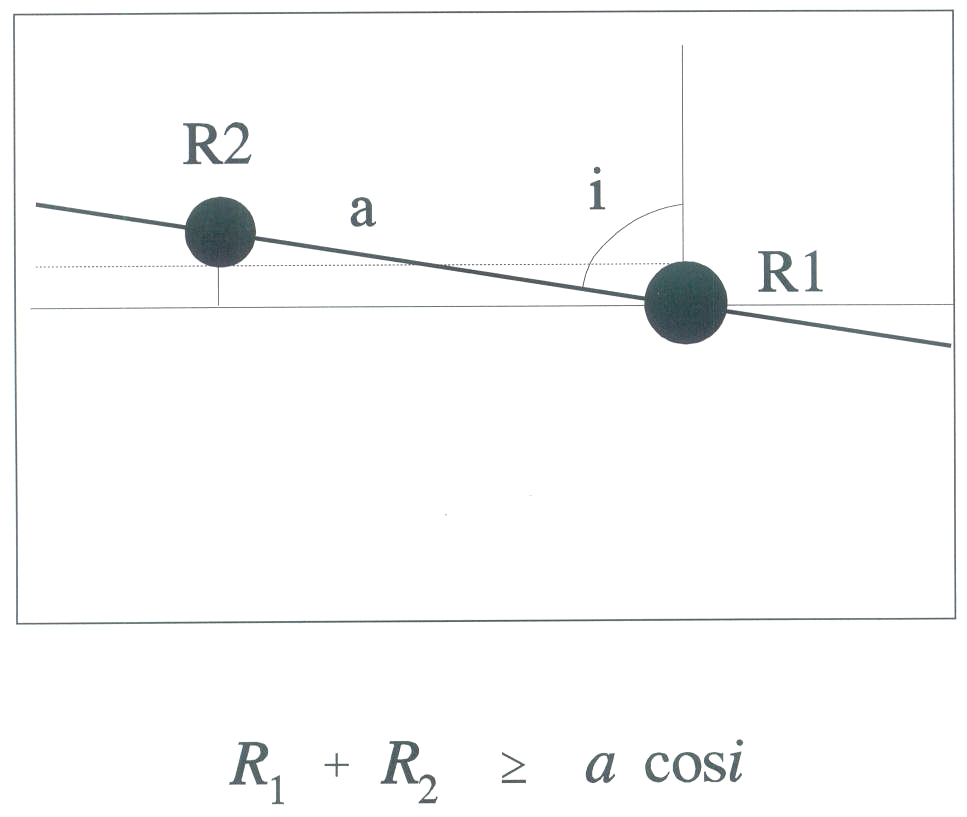
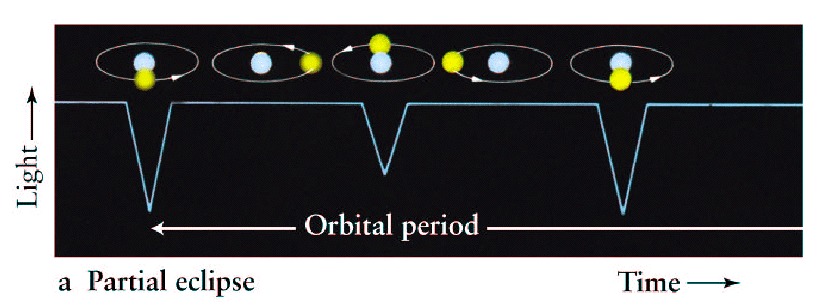
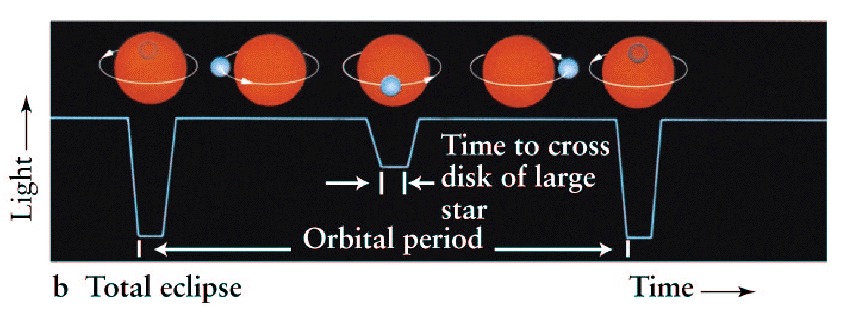
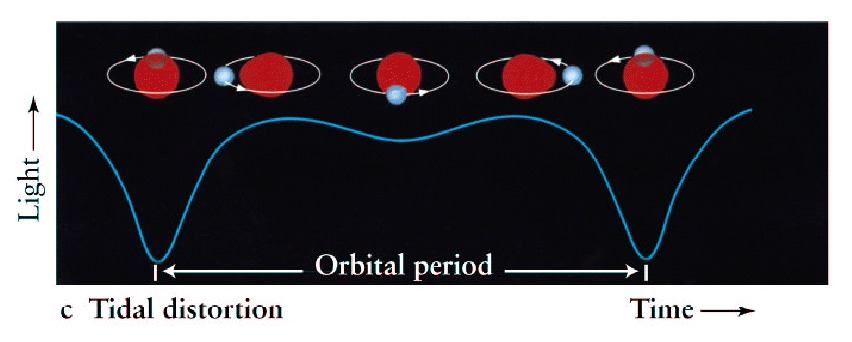
A csillagok több mint fele kettős vagy többes rendszerben található. A komponensek a közös tömegközéppont körül keringenek. Amennyiben a keringési síkhoz közeli a látóirányunk, részleges vagy teljes fedés történik, amely ideje alatt a kettőscsillag összfényessége lecsökken.

3.43. Ábra: A fedés létrejöttének geometriai feltétele (a: a pályasugár, i: a pályasík és a látóirányra merőleges közötti szög).

3.44. Ábra: A fedési fénygörbe (animáció) (http://www.astronomy.ohio-state.edu/ pogge/TeachRes/Movies162/eclbin.gif).

3.45. Ábra: A fedési fénygörbéből a sugarak becslése (animáció) (http://www.astronomynotes.com/starprop/s11.htm).

3.46. Ábra: A fedés időpontjaiból a relatív sugarak (r1/a, r2/a) meghatározása.

3.47. Ábra: Az, hogy mikor van főminimum és mellékminimum, attól függ, hogy a kisebb vagy a nagyobb hőmérsékletű csillag fedi a másikat (http://www.jimloy.com/astro/binary.htm).

3.48. Ábra: Fedési fénygörbék (Cooper-Walker 1994)

3.49. Ábra: A fedési kettősök 3 osztálya a fénygörbe alapján (http://astro.u-szeged.hu).

3.50. Ábra: A mellékminimum főminimumhoz viszonyított fázisa az ellipszispálya nagytengelyének (apszisvonalának) irányától függ. A pálya elfordulását (apszisvonal vándorlást) ez alapján lehet kimutatni (Borkovits 2009).

3.51. Ábra: A fedési fénygörbe alakját befolyásoló négy jelenség: részleges fedés, teljes fedés, árapálytorzulás, forró folt fényvisszaverődés (Kaufmann 1991).

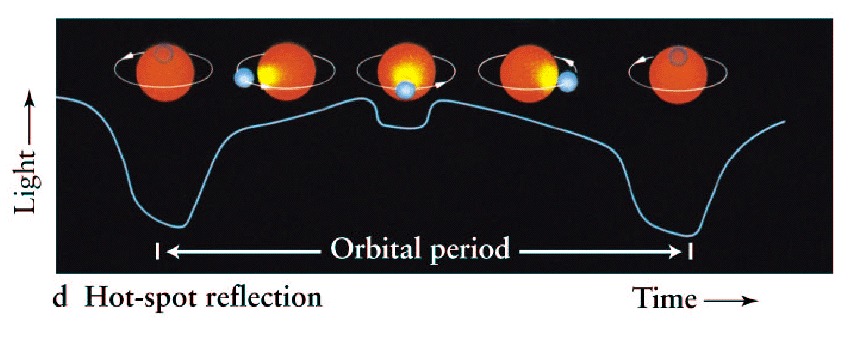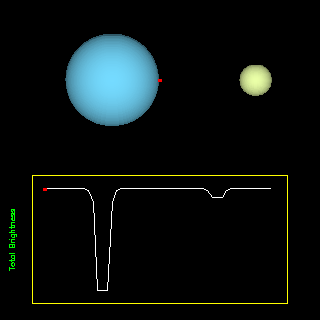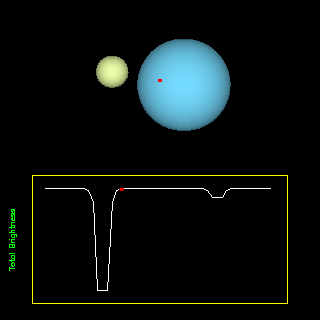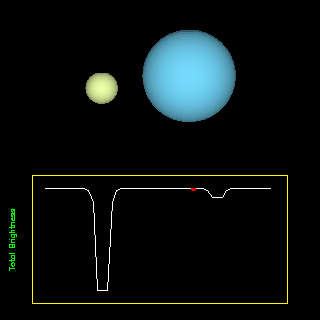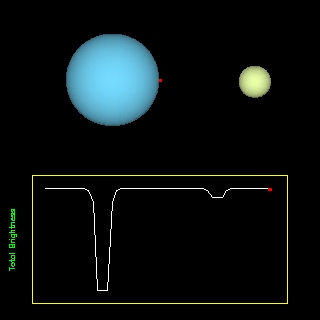
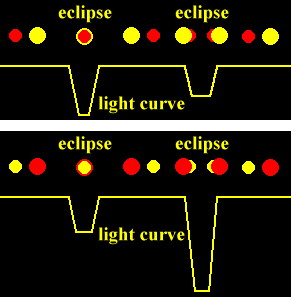
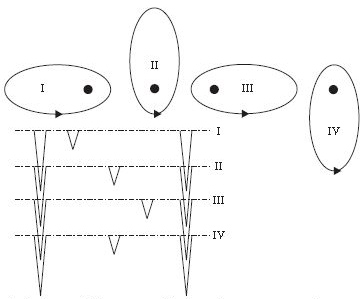
A fedési kettősök osztályozása történhet a fénygörbe alapján:

• Algol (EA), $\beta$ Lyr (EB), W UMa (EW) (3.49. ábra),

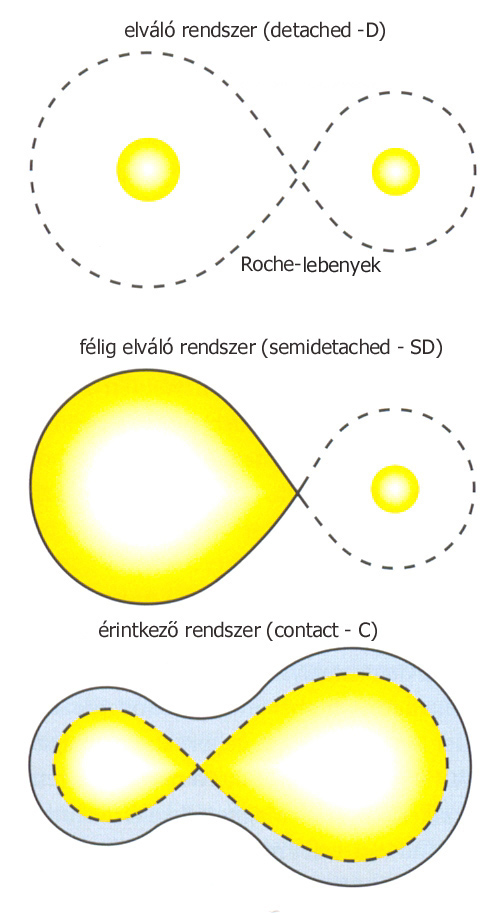
  vagy a komponensek Roche-lebenyeinek kitöltöttsége alapján:

• elváló (D), félig elváló (SD), érintkező rendszer (C) (3.52. ábra).

A kontakt rendszereknél cirkumsztelláris, mindkét komponens körüli, közös gázfelhő alakulhat ki.

3.52. Ábra: A fedési kettősök három osztálya a Roche-lebenyek kitöltöttsége alapján (Sterne und Weltraum 2008/12 alapján).

3.53. Ábra: Az Algol paradoxon: a kisebb tömegű komponens előrébb tart a fejlődésben (Mitton & Mitton 1998).

Kettős rendszereknél, különösen a fedési kettőscsillagoknál gyakran tapasztaljuk a keringési periódus változását. Ennek számos oka lehet. Az 1. pontban látszólagos, a többiben valódi a periódus megváltozása:

1. Az O-C diagram hosszú ciklusú, szinuszos függvénnyel közelíthető. Ekkor a két legvalószínűbb magyarázat:
   • Ha a fő- és a mellékminimum O-C görbéje hasonlóan, de éppen ellentétes előjellel, alternálva változik, akkor ezt az excentrikus relatív pálya körbefordulása, az apszisvonal-vándorlás (klasszikus és/vagy relativisztikus) okozhatja.
   • Ha a fő- és a mellékminimum O-C görbéje hasonlóan, azonos előjellel, egyszerre változik, akkor ennek harmadik test által okozott fényidő-effektus (LITE) lehet az oka.

2. Ha legalább az egyik komponens F-K típusú csillag, akkor az gyakran mágneses aktivitást mutat. Az Algol típusú rendszerekben a periódusváltozás okaként a mágneses aktivitási ciklust vélik magyarázatként. Arról van szó, hogy az aktív csillag alakja változik, így a gravitációs kvadrupólmomentuma is, ami kihat a keringési periódusra. Ilyenkor az aktív csillag luminozitása is változik a keringési periódus változásának periódusával megegyezően.
3. Tömeg és impulzusmomentum változása az L2 belső Lagrange-pont mentén a mágneses fékeződés (magnetic braking) által.
4. Tömegátadás a komponensek között.
5. Tömegátrendeződés az egyik vagy mindkét komponens belsejében.
6. Tömegkiáramlás, tömegvesztés a kettős rendszerből.

A szoros kettőscsillagok nagyobb része periódusváltozást mutat. A tömegátadás miatti periódusváltozás (van't Veer 1986):

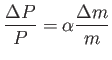$$\frac{\Delta P}{P}= \alpha \frac{\Delta m}{m}$$ (3.16)

ahol P a periódus, $m=m_1+m_2$ a két komponens össztömege, az $\alpha$ pedig tartalmazza a tömegarányt. A kettős rendszer teljes impulzusmomentuma:

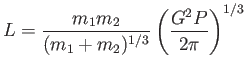$$L=\frac{m_1 m_2}{(m_1+m_2)^{1/3}}\left ( \frac{G^2 P}{2\pi} \right )^{1/3}$$ (3.17)

Ennek differenciálásával juthatunk el az $\alpha$ jelentéséhez:

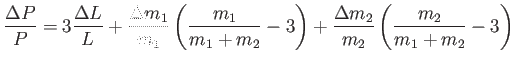$$\frac{\Delta P}{P}=3\frac{\Delta L}{L} + \frac{\Delta m_1}{m_1}\l... ...+m_2}-3\right ) + \frac{\Delta m_2}{m_2} \left ( \frac{m_2}{m_1+m_2}-3 \right )$$ (3.18)

Konzervatív tömegátadás esetén ( $\Delta L=0, \Delta m_1 = -\Delta m_2 = \Delta m$) a relatív periódusváltozás:

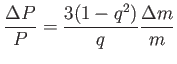$$\frac{\Delta P}{P}=\frac{3(1-q^2)}{q}\frac{\Delta m}{m}$$ (3.19)

vagyis:

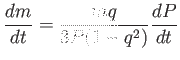$$\frac{dm}{dt}=\frac{mq}{3P(1-q^2)}\frac{dP}{dt}$$ (3.20)

ahol $q = m_2/m_1\; (m_1 > m_2)$ a tömegarány. Ha az anyag a kisebb tömegű komponensről a nagyobb tömegűre áramlik, akkor $\Delta m = \Delta m_1 > 0$, a periódus növekszik, ellenkező esetben csökken.

A tömegtranszfer hatásosságát a periódusváltozásra az

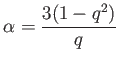$$\alpha=\frac{3(1-q^2)}{q}$$ (3.21)

értéke adja meg. Ha a q=1, azaz a két komponens egyforma tömegű, akkor $\alpha=0$, nincs változás. A csökkenő tömegaránnyal monoton növekszik a hatás a periódus változására.