Next: Periódusmeghatározó módszerek Up: Változócsillagok Previous: Szupernóvák
A periódusváltozás kimutatásának fő módszere sokáig az O-C diagram vizsgálata volt. A diagram: az idő függvényében a megfigyelt (O=observed) és a számolt (C=calculated) fénygörbemaximum (pulzálóknál) vagy minimum (fedési kettősöknél) időpontértékek különbségének ábrázolása (pl. Sterken 2005).
Az egyenessel illeszthető O-C diagram állandó periódust jelent, a parabola lineárisan változó (a felfelé nyíló növekvő, a lefelé nyíló csökkenő) periódusra, a ciklikus pedig ciklikus periódusváltozásra utal. Két, egymást metsző, különböző meredekségű egyenes esetén két, különböző periódusértékről van szó, a hirtelen periódusváltozás a két egyenes metszésének időpontjában következett be.
Az, hogy mivel illesztjük az O-C diagramot, nagyon fontos, hiszen a periódusváltozás léte és magyarázata ettől függ. Gyakori eset, hogy valaki metsző egyenesekkel, más kutató pedig parabolával közelíti ugyanazt az O-C görbét. Az első hirtelen periódusugrást, a másik folyamatos periódusváltozást jelent, amelyek mögött persze radikálisan eltérő fizikai magyarázat rejlik.
Általában az O-C diagramot egy korábbi cikkben megadott periódussal és epochával számolják, és nem próbálják változtatni a fénygörbe szélsőértékének C kalkulált időpontjait azáltal, hogy a kiszámolásukhoz használt periódus többféle értékét használnák.
| (3.22) |
ahol ![]() egy
kezdő szélsőérték időpont (epocha), P a periódus és E
a ciklusszám.
Ha a periódus lineárisan változik, akkor az O-C parabola:
egy
kezdő szélsőérték időpont (epocha), P a periódus és E
a ciklusszám.
Ha a periódus lineárisan változik, akkor az O-C parabola:
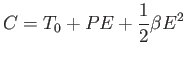 |
(3.23) |
ahol
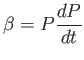 |
(3.24) |
A dP/dt periódusváltozás mértékét változatos egységekben szokták megadni: nap/ciklus, nap/nap, nap/év, másodperc/évszázad.
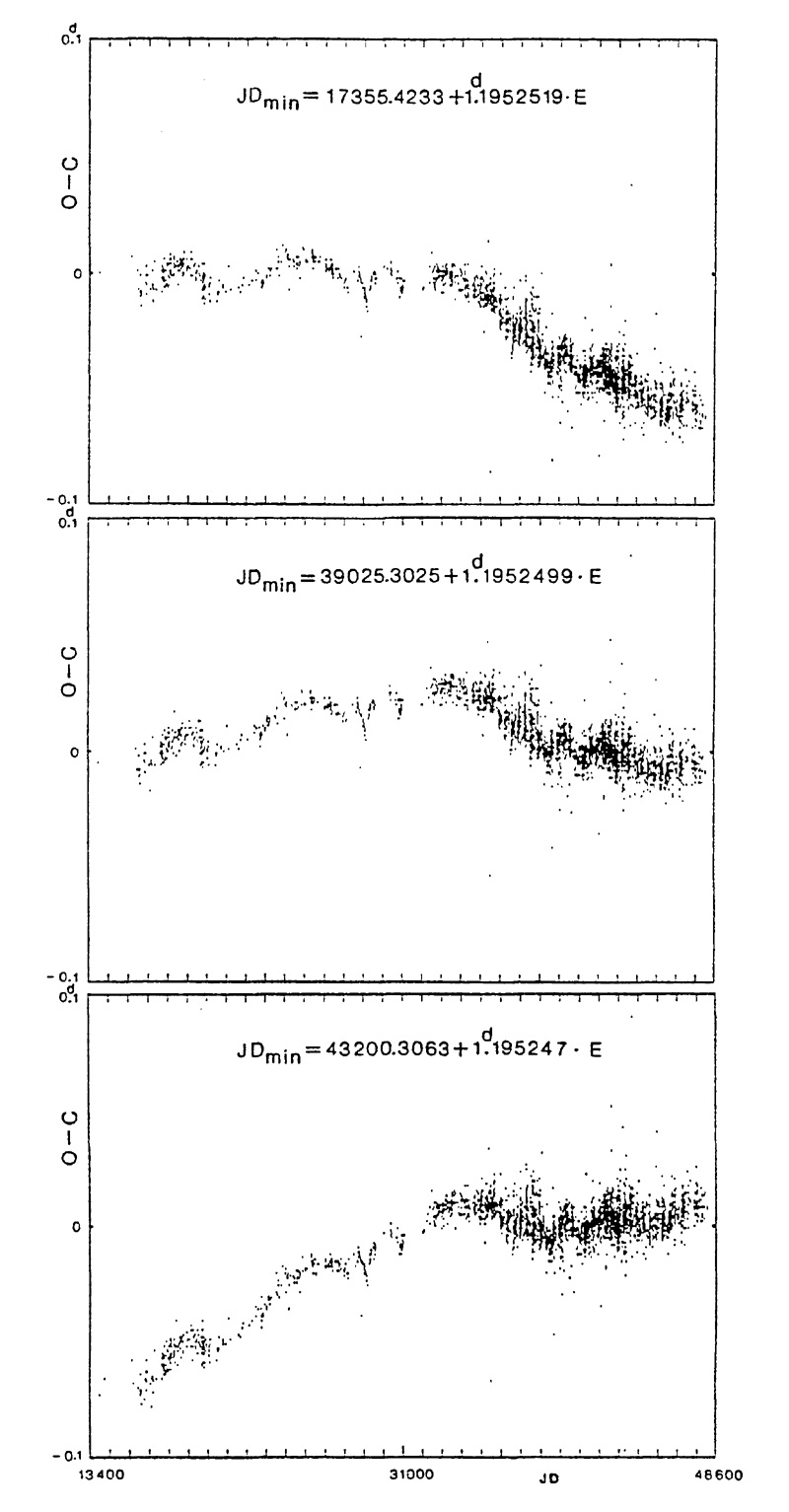
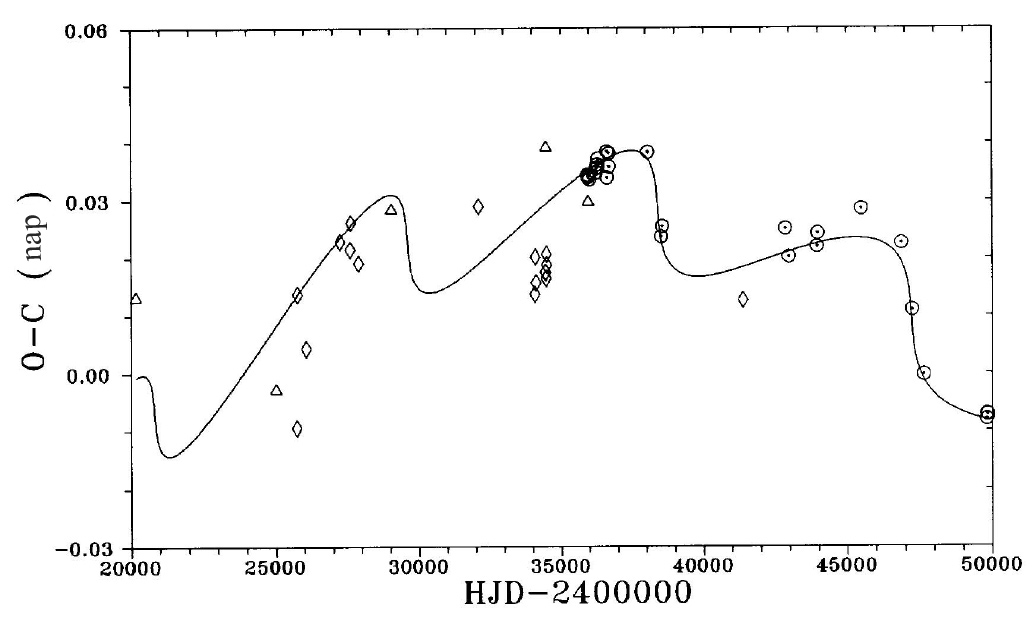
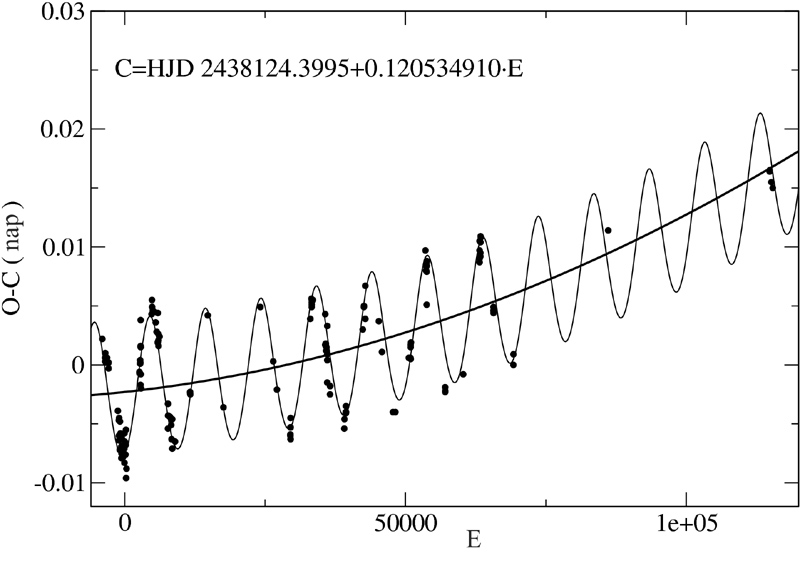
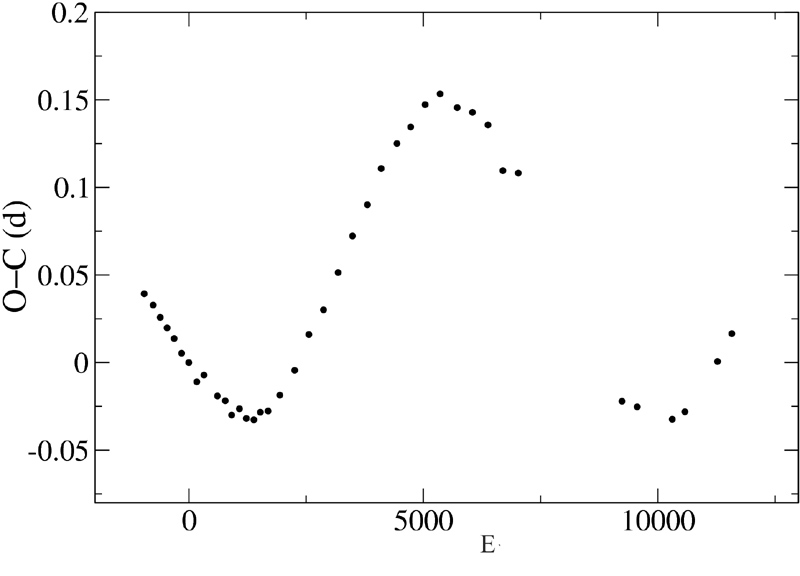
Egy fontos dologra felhívjuk a figyelmet, amit a kutatók sem nagyon ismernek és alkalmaznak. Arról van szó, hogy más-más periódussal készítve az O-C diagramot, ránézésre más alakú, menetű, jellegű lesz a görbe. A 3.86. ábra erre mutat példát. A felső és az alsó diagram két, egymást metsző egyenessel, míg a középső inkább egy lefelé nyíló parabolával illeszthető. Tehát rendkívül vigyázni kell az O-C diagram elkészítésénél és az abból levont következtetéseknél.
Az O-C módszer lényegében csak monoperiodikus jelek vizsgálatára alkalmas. Az O-C diagram értelmezésénél óvatosan kell eljárni, ha a csillag többszörös periodicitású, vagy a periódus véletlenszerűen ingadozik. Ilyen esetekben ciklusok jelenhetnek meg az O-C görbén, amelyek hamisak, nem valós változások következtében jönnek létre. Többszörös periódus esetén egy-egy periódus szerint O-C diagramot úgy érdemes készíteni, hogy előtte a többi periódussal fehérítjük az adatsort. Ez viszont megint csak problémás, ugyanis a periodikus komponensek fázisa csak kis pontossággal határozható meg.
 |
A továbbiakban még néhány példát mutatunk O-C diagramokra.
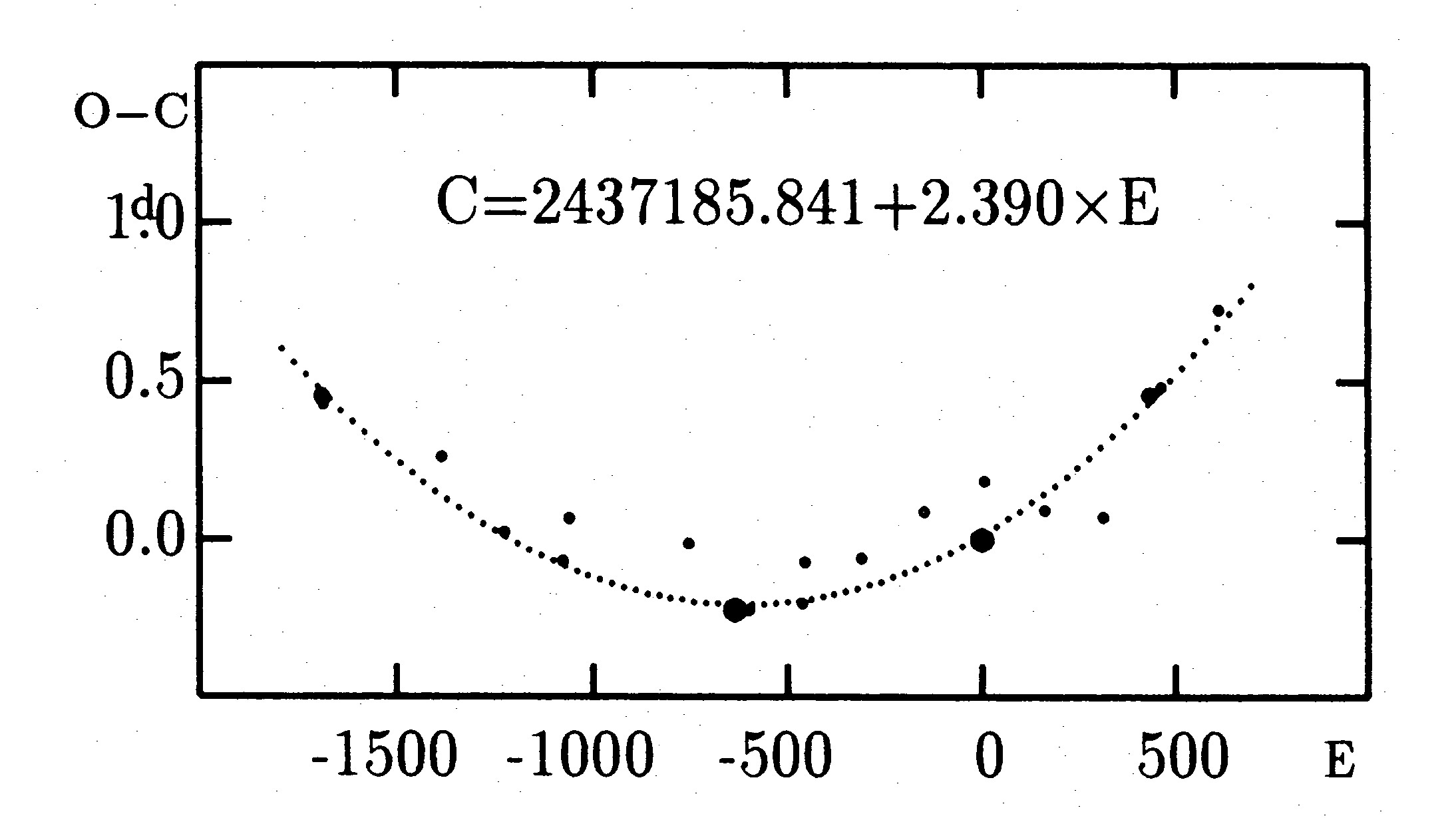 |
Az AU Peg az egyik legrövidebb periódusú kettős (
![]() ),
az árapályerőknek jelentős
szerepe lehet. Azt találtuk, hogy a periódus növekedése JD=2448000
körül megállt, sőt 2-3 ezred
napot
csökkent.
),
az árapályerőknek jelentős
szerepe lehet. Azt találtuk, hogy a periódus növekedése JD=2448000
körül megállt, sőt 2-3 ezred
napot
csökkent.
 |
 |
 |
 |
A VW Cep W UMa típusú fényes kettőscsillagot sokan és sokat mértük
(P=0,27831 nap;
![]() =7,5
mag;
=7,5
mag; ![]() =0,2
mag). A szegedi 40 cm-es távcsőnek az egyik első célpontja volt.
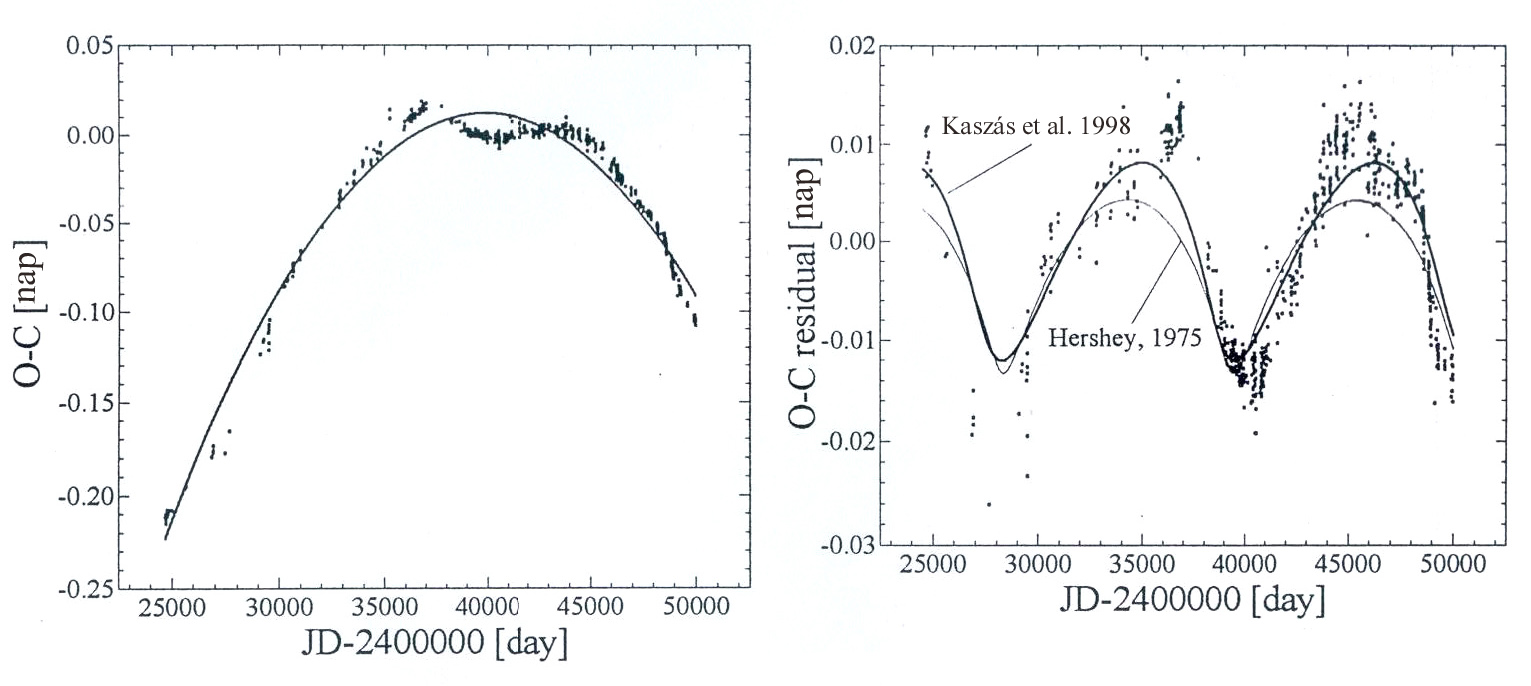
Összegyűjtöttük az összes elérhető minimumidőpontot, és
elkészítettük az O-C diagramot
(3.91. ábra). A
nagyléptékű parabolikus trendet - ami folyamatos
perióduscsökkenésnek (
=0,2
mag). A szegedi 40 cm-es távcsőnek az egyik első célpontja volt.
Összegyűjtöttük az összes elérhető minimumidőpontot, és
elkészítettük az O-C diagramot
(3.91. ábra). A
nagyléptékű parabolikus trendet - ami folyamatos
perióduscsökkenésnek (
![]() ) felel meg - levontuk. A maradékot
(reziduált) egy LITE görbével illesztettük
(
) felel meg - levontuk. A maradékot
(reziduált) egy LITE görbével illesztettük
(![]() =
30,89 év;
=
30,89 év;
![]() km; e = 0,431;
km; e = 0,431;
![]() ), ami
harmadik komponens létére utal. Látható, hogy a LITE görbe nem
illeszkedik igazán jól az adatokra,
és Hershey (1975) asztrometriai adataival sem esik egybe az
elvárható pontossággal. A LITE és az
asztrometriai megoldás között amplitúdóeltérés van, a kettő
különbsége pedig két újabb
ciklushosszra utal. Az eltérésre olyan magyarázatokat vetettünk
fel, hogy a főkomponens felszíni
mágneses aktivitási ciklust (kb. 7 év), foltosságot mutat,
valamint a 3. komponens árapályereje
perturbálhatja a periódust. A VW Cephei az egyik legtöbbet és
legalaposabban vizsgált kontakt fedési kettőscsillag.
Periódusváltozásának elemzésére
érdemes lesz visszatérni néhány év múlva, amikor már újabb 30-éves
hullámmal bővül az O-C görbe.
), ami
harmadik komponens létére utal. Látható, hogy a LITE görbe nem
illeszkedik igazán jól az adatokra,
és Hershey (1975) asztrometriai adataival sem esik egybe az
elvárható pontossággal. A LITE és az
asztrometriai megoldás között amplitúdóeltérés van, a kettő
különbsége pedig két újabb
ciklushosszra utal. Az eltérésre olyan magyarázatokat vetettünk
fel, hogy a főkomponens felszíni
mágneses aktivitási ciklust (kb. 7 év), foltosságot mutat,
valamint a 3. komponens árapályereje
perturbálhatja a periódust. A VW Cephei az egyik legtöbbet és
legalaposabban vizsgált kontakt fedési kettőscsillag.
Periódusváltozásának elemzésére
érdemes lesz visszatérni néhány év múlva, amikor már újabb 30-éves
hullámmal bővül az O-C görbe.
Szeged 2013-05-01