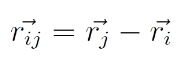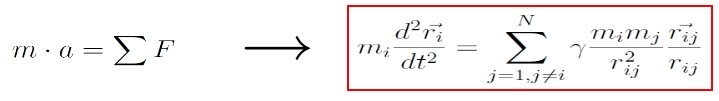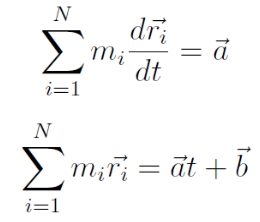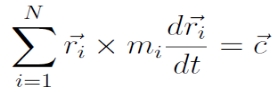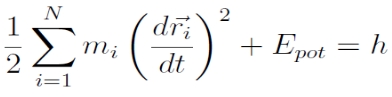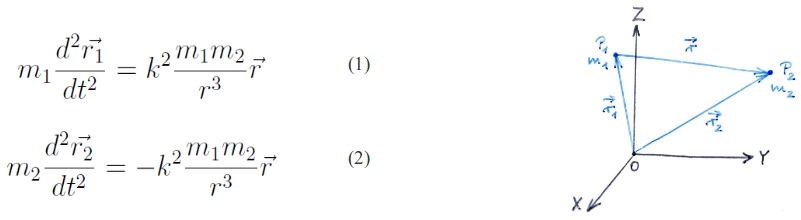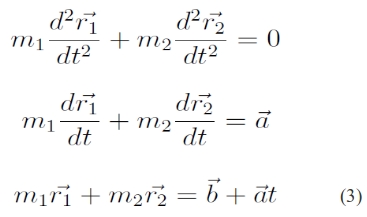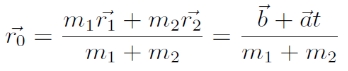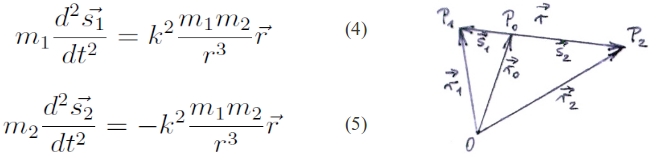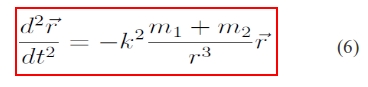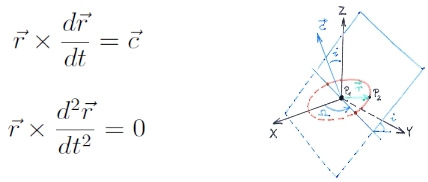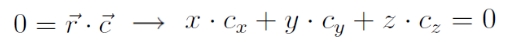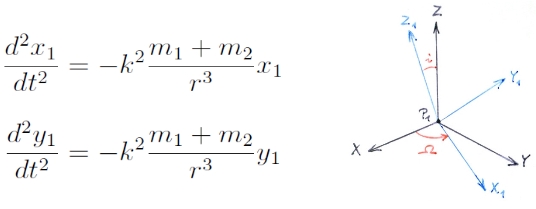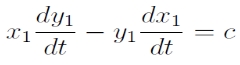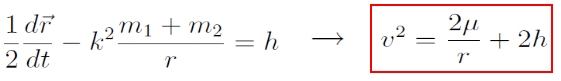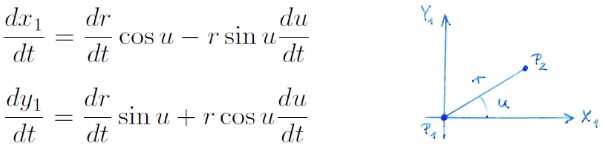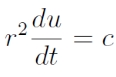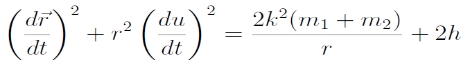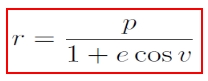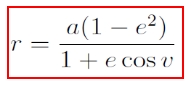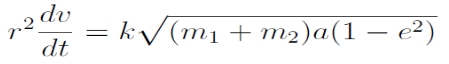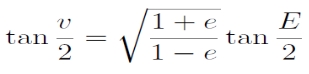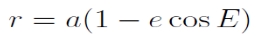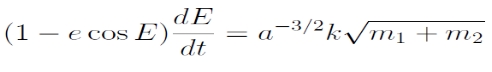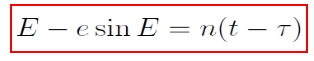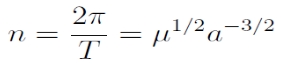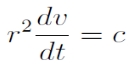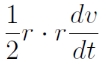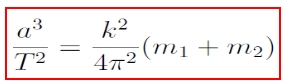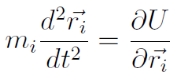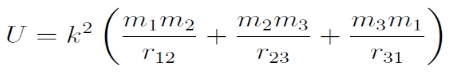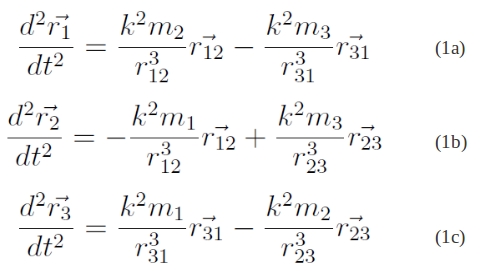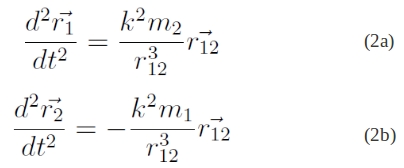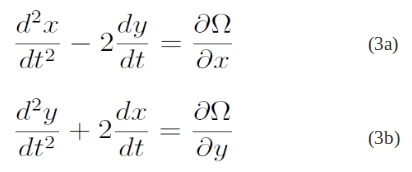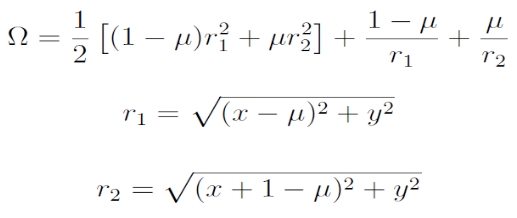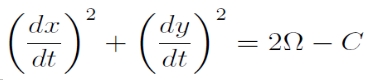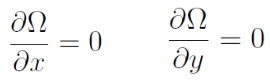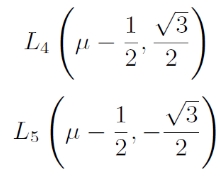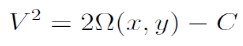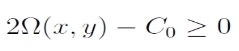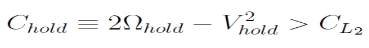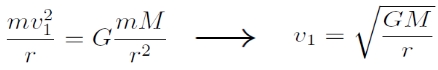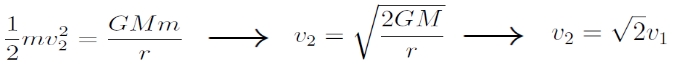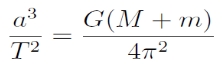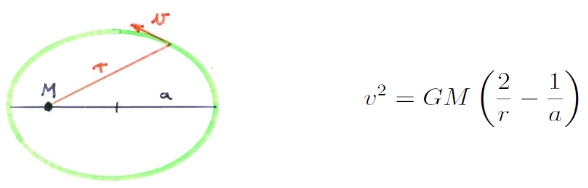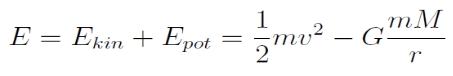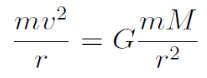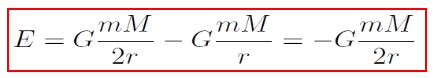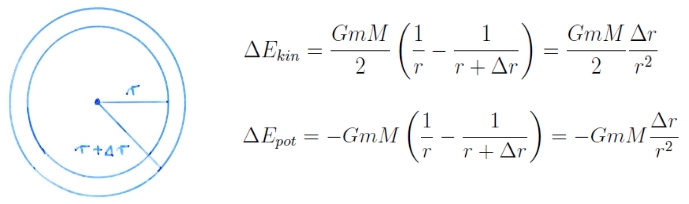Tartalom
Az ábrák listája
- 1.1. 5.1 egyenlet
- 1.2. 5.2 egyenlet
- 1.3. 5.3 egyenlet
- 1.4. 5.4 egyenlet
- 1.5. 5.5 egyenlet
- 1.6. 5.6 egyenlet
- 1.7. 5.7 egyenlet
- 1.8. 5.8 egyenlet
- 1.9. 5.9 egyenlet
- 1.10. 5.10 egyenlet
- 1.11. 5.11 egyenlet
- 1.12. 5.12 egyenlet
- 1.13. 5.13 egyenlet
- 1.14. 5.14 egyenlet
- 1.15. 5.15 egyenlet
- 1.16. 5.16 egyenlet
- 1.17. 5.17 egyenlet
- 1.18. 5.18 egyenlet
- 1.19. 5.19 egyenlet
- 1.20. 5.20 egyenlet
- 1.21. 5.21 egyenlet
- 1.22. Kúpszeletek
- 1.23. 5.22 egyenlet
- 1.24. Pályaelemek
- 1.25. 5.23 egyenlet
- 1.26. Elliptikus mozgás
- 1.27. 5.24 egyenlet
- 1.28. 5.25 egyenlet
- 1.29. 5.26 egyenlet
- 1.30. 5.27 egyenlet
- 1.31. 5.28 egyenlet
- 1.32. Kepler II. törvénye
- 1.33. 5.29 egyenlet
- 1.34. 5.30 egyenlet
- 1.35. 5.31 egyenlet
- 1.36. 5.32 egyenlet
- 1.37. 5.33 egyenlet
- 1.38. 5.35 egyenlet
- 1.39. 5.36 egyenlet
- 1.40. 5.37 egyenlet
- 1.41. 5.38 egyenlet
- 1.42. 5.39 egyenlet
- 1.43. 5.40 egyenlet
- 1.44. A korlátozott háromtest-probléma konfigurációja
- 1.45. 5.41 egyenlet
- 1.46. 5.42 egyenlet
- 1.47. 5.43 egyenlet
- 1.48. 5.44 egyenlet
- 1.49. A korlátozott háromtest-probléma egyensúlyi megoldásai, az ún. Lagrange-pontok
- 1.50. A trójai aszteroidák a Nap–Jupiter rendszer Lagrange-pontjai körül mozognak.
- 1.51. 5.45 egyenlet
- 1.52. 5.46 egyenlet
- 1.53. 5.47 egyenlet
- 1.54. A Nap–Föld rendszer Lagrange-pontjait és a körülöttük végbemehető mozgásokat, valamint a rendszer Hill-zónáit (a két égitest körüli, szférikus tartományokat) bemutató ábra).
- 1.55. 5.48 egyenlet
- 1.56. 5.49 egyenlet
- 1.57. Egy mesterséges égitest lehetséges pályái (Fizika 11-12. tk. érettségire, Mozaik Kiadó, 2008)
- 1.58. Műholdpályák a Föld körül
- 1.59. 5.50 egyenlet
- 1.60. Műholdak geostacionárius pályára (kék szín) állításának folyamata először egy LEO pálya (sárga), majd egy átmeneti pálya (narancssárga) beiktatásával.
- 1.61. A Föld és a Mars közötti Hohmann-pálya
- 1.62. Gyorsítás a gravitációs hintamanőver segítségével
- 1.63. Lassítás a gravitációs hintamanőver segítségével
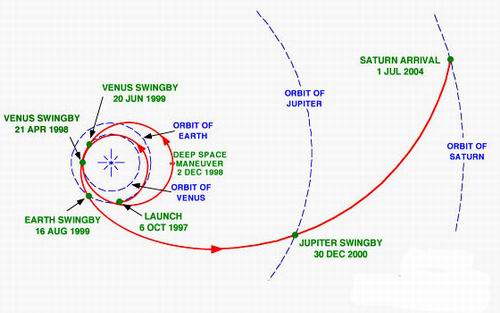
- 1.64. A Cassini-űrszonda többszörös hintamanőverekkel (2xVénusz, Föld, Jupiter) tarkított útja a Szaturnusz rendszeréig
- 1.65. 5.51 egyenlet
- 1.66. 5.52 egyenlet
- 1.67. 5.53 egyenlet
- 1.68. 5.54 egyenlet
- 1.69. 5.55 egyenlet
- 1.70. 5.56 egyenlet
- 1.71. Poynting–Robertson-effektus
Tartalom
Általános esetben, N darab gravitációsan kölcsönható test mozgásának vizsgálata az ún. N-test probléma.
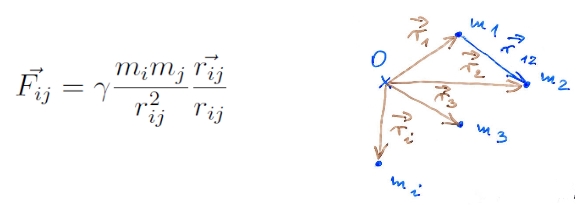
Feltevés: a rendszerben csak a gravitációs erők lépnek fel. Ekkor az i-edik és j-edik pont között ható erő:
, ahol
a két pont közötti távolságvektor.
A mozgásegyenletek a következő formában írhatóak fel:
Ez egy N tagú, másodrendű differenciálegyenlet-rendszert jelent, mely – a speciális esetektől eltekintve – csak numerikusan oldható meg.
Felírhatóak ugyanakkor a mozgásegyenletek ún. klasszikus első integráljai, melyek révén a differenciálegyenletek száma valamelyest redukálhatóak:
-
Tömegközépponti integrálok:
, ahol az a és b konstans vektorok; az egyenletek azt fejezik ki, hogy a rendszer tömegközéppontja (külső erők hiányában) egyenes vonalú, egyenletes mozgást végez, vagy nyugalomban van (ha a = 0).
-
Impulzusmomentum-integrál:
, ahol c konstans vektor, a rendszer impulzusmomentuma.
-
Energiaintegrál:
, ahol h konstans, a rendszer összenergiája.
Speciális égi mechanikai probléma, melyben két tömegpont között csak a kölcsönös gravitációs vonzóerők hatnak.
A mozgásegyenletek:
, ahol k2 = γ a gravitációs állandó. A feladat r1 = r1(t) és r2 = r2(t) egyenletek megoldása.
A két darab másodrendű differenciálegyenlet, (1) és (2) koordinátákra kiírva 6 egyenletet és összesen 12 integrációs állandót jelent.
Adjuk össze (1)-et és (2)-t (koordinátákra kiírva), majd integráljuk kétszer idő szerint:
Vezessük be a tömegközéppont fogalmát:
Ez lehetővé teszi, hogy a kéttest-problémáról áttérjünk az ún. egycentrum-problémára (OXYZ → P0XYZ koordinátarendszer-váltás).
, ahol
Így (4) és (5) átírható:
Ez pedig ugyanaz, mint (1) - (2), vagyis P2-nek P1-hez viszonyított mozgása.
Mutassuk meg, hogy ez a mozgás síkban zajlik!
Szorozzuk be a (6) egyenletet vektoriálisan a helyvektorral, majd integráljuk az idő szerint az egyenlet mindkét oldalát:
Az így kapott egyenlet bal oldala az impulzusmomentumot jelöli, ami eszerint állandó.
Skalárisan beszorozva ezt az egyenletet, és koordináták szerint kiírva ezt kapjuk:
Ez pedig a pályasík egyenlete → tehát a mozgás síkmozgás!
Legyen az alapsík a pályasík (P1XYZ → P1X1Y1Z1)!
A mozgás egyenletei:
A két egyenlet átalakításából az impulzusmomentum pedig:
A (6) egyenletet idő szerint integrálva és átrendezve az energia állandóságára vezető összefüggést kapunk, amit – felhasználva a μ = k2(m1+m2) helyettesítést – egyszerűbb formába is írhatunk:
Ha v=0 → r = - μ/h : zérósebességű felületek
Térjünk át polárkoordinátákra (x1, y1 → r, u koordináták)!
Mozgásegyenletek:
Impulzusmomentum:
Energia:
Továbbra is az r = r(t) egyenletet kell megoldanunk, azaz jelen esetben először r = r(u), majd u = u(t) egyenletet!
Ehhez az impulzusmomentum képletét felhasználva át kell térni az u szerinti deriválásra, és így kifejezni r-t az energiaegyenletből.
Felhasználva a p = c2/μ és a v = u-ω helyettesítéseket (ahol p az ún. semi-latus rectum, azaz a fókuszon átmenő, a nagytengelyre merőleges húr; ω a fenti műveletek során keletkező állandó, egyébként a pericentrum argumentuma nevű szögmennyiség, v pedig a valódi anomália nevű szögmennyiség) elvégezve az alábbi megoldást kapjuk (e az excentricitás):
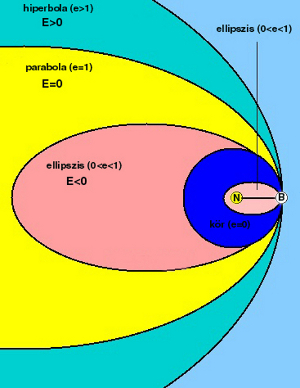
Vagyis a mozgás kúpszelet alakú pályán történik!
Ez lehet:
-
ellipszis (e < 1, h < 0) – az összenergia negatív
-
parabola (e =1, h = 0) – az összenergia nulla
-
hiperbola (e > 1, h > 0) – az összenergia pozitív
Pericentrum (a két test legkisebb távolsága): v = 0o, rmin = p / (1+e)
Apocentrum (a két test legnagyobb távolsága): v = 180o, rmax = p / (1-e)
Ellipszis és hiperbola esetén felírható: p = a (1-e2), ahol „a” a pálya félnagytengelye.
Ezt beírva a pályaegyenletbe:
Felhasználva e és p definícióját azt az érdekes összefüggést kapjuk, hogy a = - μ / 2h → vagyis az energia és a pálya félnagytengelye egymásból meghatározható!
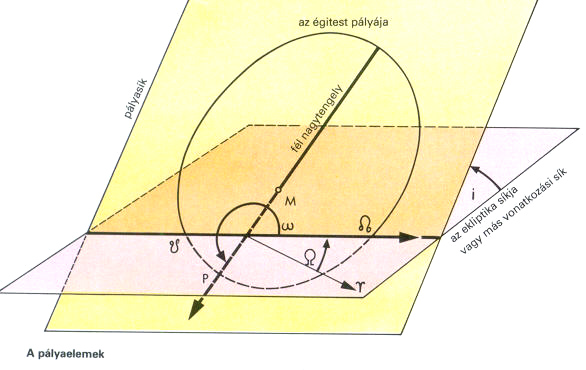
Egy égitest gravitációs terében keringő objektumok (pl. kettőscsillagok komponensei, bolygók, holdak, stb.) pályájának pontos meghatározására szolgáló paraméterek. Általában a következő hat paraméterrel adják meg egy keringő objektum pályáját:
-
i: pályahajlás vagy inklináció; a keringési sík hajlásszöge az alapsíkhoz képest
-
a: a pályaellipszis fél nagytengelye
-
e: numerikus excentricitás; a pályaellipszis lapultságát adja meg, definíció szerint: e = (a2 - b2)1/2/a , ahol b a pályaellipszis fél kistengelye
-
ω: a P pericentrum távolsága a felszálló csomótól (az az irány, ahol a kérdéses égitest pályája délről észak felé haladva metszi az alapsíkot); a keringési síkban mérjük, a pericentrum iránya és a felszálló csomó által bezárt (pozitív irányban felvett) szög nagysága
-
Ω: a felszálló csomó hossza; az alapsíkban, az alapirány és a felszálló csomó által bezárt szög nagysága
-
τ: a keringő égitest (valamelyik) pericentrum-átmenetének időpontja
A mozgás pályájának ismeretében meghatározható a mozgás időbeli lefolyása, azaz az r(t) függvény. Mivel r-nek a v valódi anomáliától való függését ismerjük, a feladat a v(t) függvény meghatározása. Írjuk fel az impulzusmomentum-egyenletet v felhasználásával:
Ez az egyenlet azonban véges formában nem integrálható, így szükség van v helyett egy új változó bevezetésére. Láttuk, hogy a mozgás pályája ellipszis, parabola vagy hiperbola, az energiától függően. Az új változó bevezetése függ a pálya típusától. Mivel a gyakorlatban elliptikus pályák fordulnak elő leggyakrabban (pl. bolygók mozgása), itt csak az elliptikus mozgás esetét tárgyaljuk.
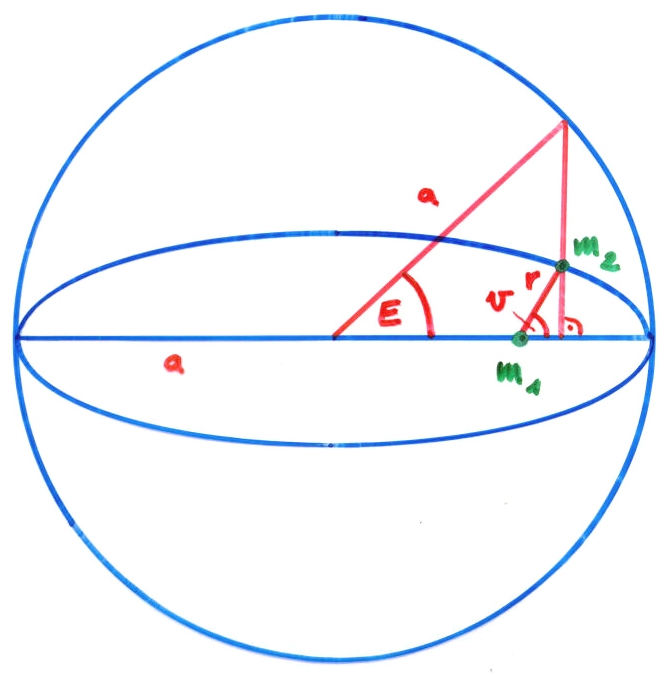
Elliptikus mozgás esetén a v valódi anomália helyett vezessük be az E excentrikus anomáliát. Rajzoljuk meg ehhez az ellipszis főkörét, ami egy a sugarú kör az ellipszis középpontja körül. Az m2 tömegponton át húzzunk egyenest az ellipszis nagytengelyére merőleges irányban, így kapunk egy metszéspontot a főkörön. Ezt a metszéspontot az ellipszis középpontjával összekötve a kapott szög az E excentrikus anomália.
Trigonometrikus azonosságok felhasználásával kiderül, hogy v és E kapcsolata csak e-től függ:
Az r helyvektor nagysága pedig így adható meg:
Beírva E-t v helyére, az impulzusmomentum-egyenlet így alakul:
Az egyenletet integrálva megoldásként az ún. Kepler-egyenletet kapjuk:
, ahol τ a pericentrum-átmenet időpontja, n pedig az ún. középmozgás:
A transzcendens Kepler-egyenletből E = E(t) meghatározható, de csak egy végtelen sor formájában (numerikus módon megoldható).
A kéttest-probléma alkalmazásával a Johannes Kepler által felállított bolygómozgási törvények az eredetinél jóval komolyabb matematikai alapot kapnak.
Hasonlítsuk össze az egyes törvények Kepler által kimondott alakját a kéttest-probléma formalizmusa révén levezethető eredményekkel!
-
I. törvény: A bolygók a Nap körül ellipszispályákon keringenek, melyek egyik fókuszában a Nap helyezkedik el.
Ahogy az előző fejezetben láttuk, a kéttest-probléma leírásából következik, hogy a pályák alakja kúpszelet, ami az összenergia függvényében ellipszis, parabola vagy hiperbola lehet. A bolygók (melyekre Kepler eredetileg kimondta törvényét) valóban ellipszispályákon keringenek a Nap körül (illetve más csillagok körül), de kisebb égitestek (üstökösök, aszteroidák, űrszondák) esetében gyakori a parabola vagy hiperbola alakú pálya.
-
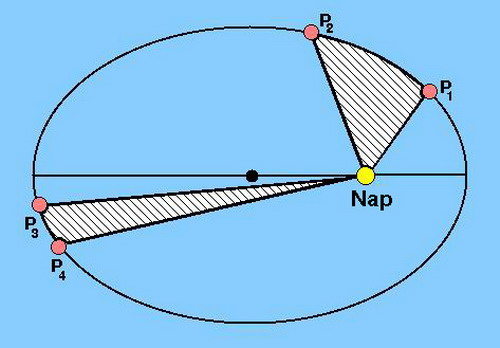
II. törvény: A bolygók vezérsugara (a bolygókat a Nappal összekötő szakasz) az idővel arányos területeket súrol.
Más szavakkal: a felületi sebesség a mozgás során állandó.
Szintén az előző fejezetben láttuk, hogy felírható az impulzusmomentum megmaradása:
Felhasználva a v = u-ω helyettesítést (ahol tehát ω a pericentrum argumentuma, v pedig a valódi anomália), valamint azt, hogy ω állandó, ez átírható:
Mivel a felületi sebesség definíciója:
, ezért az előzőekből pontosan az következik, hogy ez állandó.
-
III. törvény: A bolygók Naptól számított távolságainak harmadik hatványai úgy aránylanak egymáshoz, mint a keringési idők négyzetei.
Felhasználva a redukált tömeg μ = k2(m1+m2) definícióját, valamint a
középmozgás-definíciót, megkapjuk a
összefüggést, ami jóval többet mond, mint az eredeti Kepler-törvény: megadja, hogy az arányosság a két égitest tömegétől függ. Nap-bolygó rendszer esetében a bolygó tömege általában elhanyagolható, így az arányossági tényező a Nap körül keringő minden égitestre ugyanakkora lesz – a nagyon pontos égi mechanikai számításokhoz viszont szükség van a kisebb tömeg pontos ismeretére is.
Az égi mechanika leghíresebb problémája az ún. háromtest-probléma, azaz három tömegpontnak tekinthető test mozgásának meghatározása abban az esetben, ha köztük csak a gravitációs vonzóerők hatnak. Bár a feladat látszólag egyszerű, valójában a megoldások nem speciális esetekben igen bonyolultak.
Az általános háromtest-probléma mozgásegyenleteinek egységes formulája:
, ahol U az égi mechanikában használatos erőfüggvény (a potenciális energia -1-szerese):
Az első egyenlet egy tizennyolcadrendű differenciálegyenlet-rendszer, amely a klasszikus első integrálok felhasználásával hatodrendűvé redukálható.
A továbbiakban egy speciális esetet, az ún. korlátozott háromtest-problémát vizsgáljuk.
A háromtest-probléma speciális esete, melyben az egyik tömegpont tömegét elhanyagolhatóan kicsinek választjuk a másik kettőhöz képest.
Írjuk fel a mozgásegyenleteket:
Az egyik tömegpont (legyen az m3) tömege tartson a nullához (de ne érje el azt)! Így az első két egyenlet felírható:
(2a), (2b) és (1c) egyenletek írják le a mozgást; az első kettő közelítő, míg a harmadik pontos. A (2a)-(2b) egyenletek megoldása az, hogy az m1, m2 a közös tömegközéppont körül kúpszelet alakú pályán mozog. Az m1, m2 tömegektől és az r1, r2, r3 vektoroktól függően több esetet különböztetünk meg:
-
Korlátozott háromtest-probléma: A pálya kör, r1, r2, r3 mindig egy síkban vannak. Ha r3 az (r1, r2) síkon kívül is tartózkodhat (azaz térbeli mozgást is végezhet), akkor térbeli korlátozott háromtest-problémáról beszélünk (pl. nagy pályahajlású kisbolygók esetében).
-
Elliptikus korlátozott háromtest-probléma: A két fő tömegpont relatív pályája ellipszis. Szintén van síkbeli és térbeli változata. Általában jobb közelítést ad az előző esetnél.
-
Perturbált kéttest-probléma: A két fő tömegpont közül az egyik tömege (pl. m1) jóval kisebb a másik tömegénél.A harmadik test mozgását ekkor elsősorban m1 gravitációs vonzása határozza meg, melyet m2 kis mértékben befolyásol. Főleg a bolygók egymásra gyakorolt perturbációinak vizsgálatában alkalmazható.
-
Kétcentrum-probléma: m1 és m2 legyen rögzített helyzetű (tehát a 2a-2b egyenletek most nem érvényesek!), a harmadik test pedig ezek gravitációs terében mozog. A probléma így analitikusan megoldható. Jellemzően a Föld gravitációs terében keringő műholdak mozgását lehet jól leírni ezen a módon.
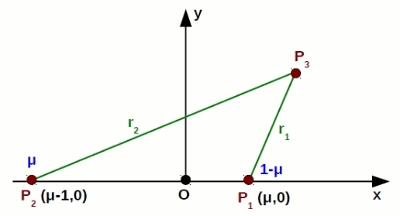
Írjuk le a korlátozott háromtest-problémát forgó koordináta-rendszerben:
, ahol
, μ = m2/(m1+m2) pedig az ún. redukált tömeg; Ω-t effektív potenciálnak nevezik. Fontos, hogy itt most a „t” szerinti differenciálás nem idő, hanem a két fő tömegpont középanomáliája szerint zajlik.
Ha a (3a) és (3b) egyenleteket dx/dt-vel és dy/dt-vel rendre megszorozzuk, összeadjuk és integráljuk, megkapjuk az ún Jacobi-integrált, a korlátozott háromtest-probléma egyetlen ismert integrálját; C a Jacobi-konstans:
A korlátozott háromtest-probléma forgó koordináta-rendszerben vett mozgásegyenleteinek az
feltételt kielégítő megoldásait egyensúlyi megoldásoknak nevezzük, melyeket a
egyenletek adják.
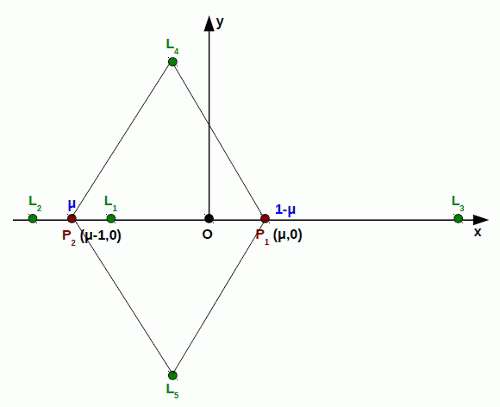
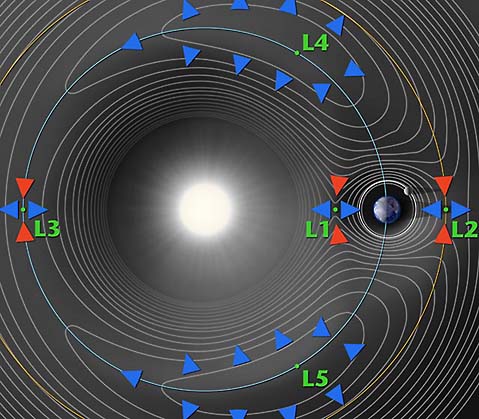
Megoldásként 5 pontot kapunk, melyeket Lagrange-pontoknak nevezünk. Ezekből három az x tengelyen van, az L4 és L5 pontok pedig egyenlő oldalú háromszögeket alkotnak a (μ-1,0) és (μ,0) pontokkal – ezek koordinátái:
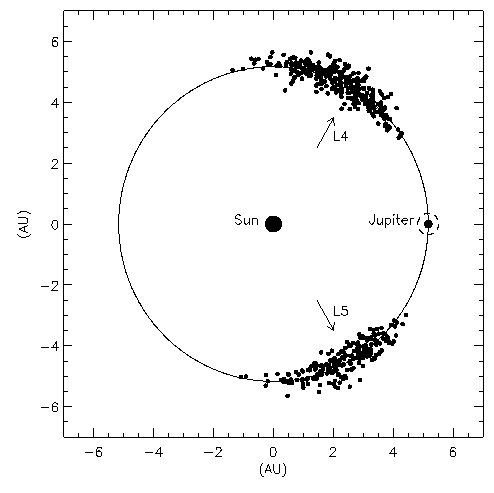
Az első három Lagrange-pont sohasem stabil (azaz az onnan kimozdított 3. test nem tér oda vissza), míg a 4-es és 5-ös lehet stabil, ha nagy a különbség a két fő tömeg között. Utóbbiak körül nagy amplitúdójú mozgás is lehetséges (mind rövid, mind hosszú periódussal). Ezeket librációs mozgásnak, így az L pontokat librációs pontoknak is nevezik. A Nap–Föld rendszer Lagrange-pontjaiban több műhold és űrtávcső is működik (működött) (pl.L 1: SOHO, SDO, L2: Herschel, WMAP, Planck), míg a Jupiter–Nap rendszer L4 és L5 librációs pontjaiban keringenek az ún. trójai kisbolygók.
A Jacobi-integrál felhasználásával meghatározhatóak a mozgás számára lehetséges tartományok. Legyen a harmadik tömegpont sebessége V, ekkor:
A szükséges kezdőfeltételek ismeretében a kezdeti állapotra érvényes C0 konstans meghatározható. Mivel V2 nemnegatív szám, ezért C0 esetén mozgás csak ott lehetséges, ahol:
Azokat a görbéket, melyek mentén a fenti egyenlőtlenség nullát ad, zérósebességű vagy Hill-görbéknek nevezzük; ezek választják el a mozgás számára lehetséges és tiltott tartományokat (térbeli korlátozott háromtest-probléma esetén Hill-felületekről beszélünk).
A Hill-féle stabilitás különösen érdekes a csillag-bolygó-hold hármas rendszerekben. Ahhoz, hogy egy hold stabilan tudjon keringeni egy bolygó körül, a pályájához tartozó Jacobi-konstansnak nagyobbnak kell lennie, mint a csillag-bolygó rendszer L2 pontjához tartozó Jacobi-konstansnak:
A Nap–Föld–Hold rendszer esetében Chold = 3,0012, míg CL2 = 3,0009; tehát a Hold mozgása Hill-értelemben stabil.
A műholdak és űrszondák sokféle pályán helyezkedhetnek el, és rendkívül sokrétű feladatot láthatnak el. Ahhoz, hogy egy testet Föld körüli pályára állítsunk, vagy a bolygóközi térbe küldjünk, a különböző, ún. kozmikus sebességeknél nagyobb értékre kell felgyorsítanunk azt:
-
I. kozmikus sebesség (körsebesség): Az a sebesség, mellyel indítva egy test (pl. műhold) az adott égitest (pl. a Föld) körüli pályára képes állni. Körpálya esetén a testet pályán tartó centripetális erő (mely jelen esetben a gravitációs erővel egyezik meg), egyszerűen felírható:
Értéke egy Földről indított test esetében 7,9 km/s.
-
II.kozmikus sebesség (szökési sebesség): Az a minimális sebesség , mellyel a test "elhagyhatja" az adott égitest gravitációs terét, közeléből a végtelenbe távozik. Ehhez a testnek mozgási energiájának legalább akkorának kell lennie, mint a lokális gravitációs potenciális energia:
Szokás még definiálni ún. III. és IV. kozmikus sebességet is, melyek a Naprendszer, illetve a Tejútrendszer elhagyásához szükséges minimális sebességeket jelentik (Földről indított űrszonda esetében ezek értéke 16,6 km/s, illetve ~ 500 km/s). Megjegyzendő, hogy az eddigi leggyorsabb, ember alkotta űrszondák (a Naprendszer távoli vidékei felé indított Pioneer-10 és -11, a Voyager-1 és -2, valamint a New Horizons) nagyjából a III. kozmikus sebesség körüli értékkel haladnak a bolygóközi térben.
1.57. ábra - Egy mesterséges égitest lehetséges pályái (Fizika 11-12. tk. érettségire, Mozaik Kiadó, 2008)
 |
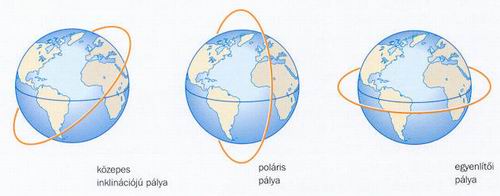
A Föld körül keringő műholdak és egyéb égitestek különböző pályákon mozoghatnak. A pályák csoportosítása elsősorban az egyes pályaelemek alapján történik:
-
excentricitás alapján: körpálya (e=0), elliptikus pálya
-
inklináció alapján: egyenlítői pálya (i=0o), közepes inklinációjú pálya, poláris pálya (i=90o)
-
félnagytengely (magasság) alapján: LEO (Low Earth Orbit, 0 < h < 2000 km), MEO (Medium Earth Orbit, 2000 km < h < 35 768 km), GEO (Geosynchronous Earth Orbit, h = 35 768 km), HEO (High Earth Orbit, h > 35768 km).
A h = 35 768 km-es magassághoz tartozó speciális pálya az ún. geoszinkron pálya: ennek jellegzetessége, hogy a rajta mozgó műhold keringési ideje megegyezik a Föld tengelyforgási idejével (T = 24 óra = 86400 s):
Innen a félnagytengely: a = 42 164 km, a földfelszín feletti magasság pedig: h = a – RFöld = 42 164 km – 6376 km = 35 768 km.
Ha a pálya excentricitása és inklinációja is 0, tehát a szonda 35 768 km magasságú körpályán kering az Egyenlítő síkjában, akkor geostacionárius pályáról beszélünk: az így keringő műhold mindig a Föld egy adott pontja fölött tartózkodik, látszólag mozdulatlan; sok távközlési műhold mozog ilyen pályán (az adatátvitel könnyebbsége miatt).
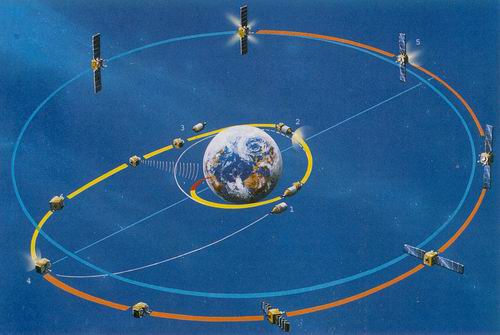
1.60. ábra - Műholdak geostacionárius pályára (kék szín) állításának folyamata először egy LEO pálya (sárga), majd egy átmeneti pálya (narancssárga) beiktatásával.
 |
Léteznek további speciális pályák, is, mint pl. a napszinkron pálya (ekkor a műhold képes követni a Nap irányának a Föld keringéséből adódó, naponta kb. 1 fokos változását, így a műhold az adott terület fölött mindig ugyanabban a napszakban repülhet el – ez idális pl. a térképező műholdak számára), vagy a különböző távközlési és navigációs műholdcsaládok pályái (GPS, Molnyija stb.).
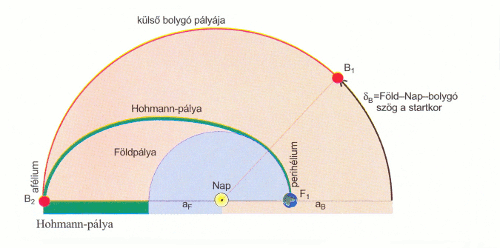
A bolygóközi térben mozgó űrszondák számára két fontos tényező alakítja ki a pályák alakját: vagy a legrövidebb idő alatt, vagy a legkisebb energiafogyasztással kell eljutniuk céljukhoz. Utóbbi esetben a Hohmann-ellipszis nevű átmeneti pályát alkalmazzák: ennek perihéliumtávolsága a Naphoz közelebbi bolygó, aphélium-távolsága a Naptól távolabbi bolygó fél nagytengelyével egyezik meg; a pálya fél nagytengelye a már említett két bolygó pályája fél nagytengelyének számtani közepe.
Ennek a pályának az a hátránya, hogy egyrészt nem a leggyorsabb úton juttatja a szondát a célbolygóhoz, másrészt az indítás nem történhet tetszőleges időpontban, csak az ún. indítási ablakokban (ezek azok az időszakok, mikor az űrszondát indítva az úgy érkezik a célpont távolságába, hogy a bolygó is éppen akkor érjen pályája azon szakaszába). Ezek jellemzően néhány hetes időszakok, melyek pl. a Mars esetében kb. két évente követik egymást.
A bolygóközi repülések során az ún. gravitációs hintamanőverek révén lehetőség van a szondák sebességének, illetve a mozgás irányának megváltoztatására. Ekkor a szondának annyira meg kell közelítenie egy bolygót, hogy bekerüljön annak gravitációs terébe, de sebessége még meghaladja az ottani szökési sebességet. Így a pálya parabola alakú lesz, és a szonda sebessége – a bolygó gravitációs teréből nyert impulzusmomentum révén – nagyobb lesz, mint eredetileg volt. Ha az a cél, hogy a szonda pályára álljon a bolygó körül, akkor a relatív sebességet fékezéssel csökkenteni kell.
Vizsgáljunk egy M tömegű test körül ellipszis alakú pályán keringő, m tömegű testet (például egy, a Föld körül keringő műholdat)! A keringés sebessége összefügg a két test pillanatnyi távolságával, r-rel:
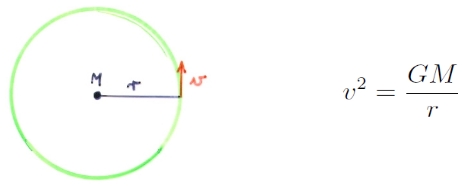
Speciális, kör alakú pálya esetén:
Az ún. égi mechanikai paradoxon lényege: gyorsítás esetén a keringő test végeredményképpen lassul, fékezés esetén pedig gyorsul!
Magyarázat:
Az egyszerűség kedvéért vegyünk kör alakú pályán történő mozgást, és számoljuk ki a keringő testnek a kinetikus és a potenciális energia összegéből előálló teljes mechanikai energiáját:
A testet a körpályán tartó (centripetális) erő nem más, mint a gravitációs erő:
Ebből a sebességet kifejezve és visszahelyettesítve az energiaegyenletbe:
Vagyis a fenti összefüggések alapján E ~ -1/r és v ~ r-1/2.
Fékezés esetén: az összenergia csökken → a pályasugár is csökken → tehát a keringési sebesség nő!
Gyorsítás esetén: az összenergia nő → a pályasugár is nő → tehát a keringési sebesség csökken!
Megvizsgálva a kinetikus és a potenciális energia változását a pályasugár ∆r mértékű megváltozásakor azt kapjuk, hogy a potenciális energia változása kb. kétszerese a kinetikusénak (ebből fakad a paradoxon létrejötte):
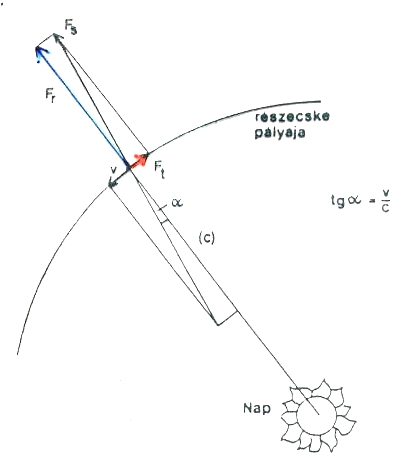
Az égi mechanikai paradoxon egyik legszemléletesebb példája a Naprendszerben az ún. Poynting–Robertson-effektus.
A Nap körül v sebességgel keringő meteorikus testre a sugárnyomás az aberráció miatt nem pontosan radiális, hanem azzal α szöget bezáró irányban hat (ahol az α szög nagysága a keringési sebesség és a fénysebesség hányadosától függ). A sugárnyomás érintő irányú összetevője a testet fékezi, emiatt – az égi mechanikai paradoxon értelmében – a test mozgása gyorsul, és fokozatosan közeledik a Naphoz.