Roche-határ

A Roche-határtól távol a kísérő égitest gyakorlatilag gömb alakú.

A Roche-határ közelében az árapály-erő miatt torzul az alakja.

A Roche-határnál a hold saját gravitációja a bolygó árapályereje ellenében már nem tudja összetartani az anyagát, ezért szétdarabolódik.

A bolygóhoz közelebbi darabok gyorsabban mozognak, mint a távolabbiak.

A törmelékdarabok eltérő keringési sebessége miatt egy gyűrű alakul ki.

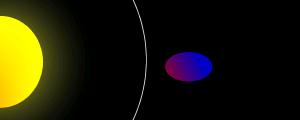
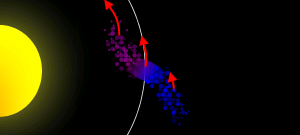
A Roche-határ, vagy Roche-sugár az a távolság egy bolygó centrumától, amelyen kívül keringhetnek körülötte holdak. A Roche-határon belül a bolygótól származó gravitációs árapályerő szétszedi, feldarabolja a holdat, és egy törmelékgyűrű alakul ki. Az elnevezés Édouard Roche francia csillagászra utal, aki 1848-ban elsőként számolta ki ennek az elméleti határnak az értékét.

Megjegyzendő, hogy a Roche-határ nem tévesztendő össze a szoros kettőscsillagoknál fontos Roche-lobe (üreg) vagy Roche-felület fogalmával, amelyet szintén Édouard Roche-ról neveztek el.

A Roche-határ meghatározása

A Roche-határ függ a hold szilárdságától. Egy teljesen szilárd hold megtartja alakját, mialatt az árapályerő szétaprítja. Egy nagyrészt folyékony anyagú hold erősen deformálódik az árapály hatása alatt. A valódi holdak valahol e két határeset között vannak.

Szilárd anyagú holdak

Egy szilárd, gömb alakú hold Roche-határánakkiszámításánál több közelítést tehetünk, melyek jelentősen leegyszerűsítik a feladatot. Feltesszük, hogy a hold végig megtartja gömb alakját, és eltekintünk a bolygó alakjának deformációjától, a hold forgásától és alakjától.

Egy szilárd, gömb alakú hold esetén a d Roche-határ:

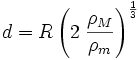
ahol R a bolygó sugara, ρ_M a bolygó sűrűsége és ρ_m a hold sűrűsége.

Ha a hold több mint kétszer sűrűbb a bolygónál (ami előfordul az óriásbolygóknál), akkor a Roche-határ a bolygó felszíne alatt van.

A képlet kiszámítása

A Roche-határ közelítő meghatározásához tekintsünk egy kis u tömeget a hold bolygó felé eső oldalán. Két, ellentétes irányú erő hat erre az u tömegre: a hold gravitációs ereje a hold középpontja felé, és a bolygó vonzóereje a bolygó felé. Utóbbi esetében csak az árapályerőt vesszük figyelembe, mivel a hold (szabadon esve) kering a bolygó körül.

Az m tömegű és r sugarú hold F_G gravitációs vonzóereje az u felszíni tömegre a Newton-törvény alapján:

$F_G = \frac{Gmu}{r^2}$

A bolygó F_T árapály-ereje az u tömegre (d a távolság a két égitest centruma között):

$F_T = \frac{2GMur}{d^3}$

A Roche-határ ott van, ahol ez a két erő megegyezik:

azaz

$\frac{Gmu}{r^2} = \frac{2GMur}{d^3}$

Innen kifejezhető a d Roche- határ:

$d = r \left( 2 M / m \right)^{\frac{1}{3}}$

Azonban jó lenne, ha a hold r sugara nem szerepelne a képletben, ezért helyette a sűrűségeket vezetjük be.

Az R sugarú bolygó M tömege:

$M = \frac{4\pi\rho_M R^3}{3}$

Hasonlóan az r sugarú hold m tömege:

$m = \frac{4\pi\rho_m r^3}{3}$

A tömegek ezen kifejezését behelyettesítve, a Roche-határ:

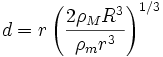
$d = r \left( \frac{ 2 \rho_M R^3 }{ \rho_m r^3 } \right)^{1/3}$

azaz:

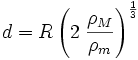
$d = R\left( 2\;\frac {\rho_M} {\rho_m} \right)^{\frac{1}{3}}$

Folyékony holdak

A Roche-határ pontosabb kiszámításánál figyelembe vesszük a hold alakjának deformációját is.

A számítás igen bonyolult, és csak numerikusan lehet megoldani. Roche a következő értéket kapta:

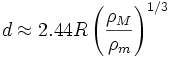
$d \approx 2.44R\left( \frac {\rho_M} {\rho_m} \right)^{1/3}$

Pontosabb a közelítés, amikor figyelembe vesszük a bolygó lapultságát és a hold tömegét is:

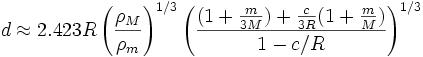
$d \approx 2.423 R\left( \frac {\rho_M} {\rho_m} \right)^{1/3} \left( \frac{(1+\frac{m}{3M})+\frac{c}{3R}(1+\frac{m}{M})}{1-c/R} \right)^{1/3}$

ahol c / R a bolygó lapultsága.

A folyékony közelítés alkalmazható a laza összetételű kis égitestekre is, mint az üstökösök. Például a Shoemaker-Levy 9 üstökös 1992 júliusában szétesett, amikor a Jupiterhez túl közel került. A következő megközelítéskor, 1994-ben a darabjai becsapódtak a Jupiter légkörébe. A Shoemaker-Levy 9-et 1993-ban fedezték fel. A pályaszámítások szerint néhány évtizeddel korábban fogta be a Jupiter.

Roche-határok a Naprendszerben

központi égitest	sűrűség (kg/m³)	sugár (km)
Nap	1408	696000
Jupiter	1326	71492
Föld	5513	6378
Hold	3346	1738
Szaturnusz	687	60268
Uránusz	1318	25559
Neptunusz	1638	24764

Ezeket az adatokat felhasználva könnyen kiszámíthatók a Roche-határok akár szilárd, akár folyékony égitestekre. Az üstökösök átlagos sűrűsége 500 kg/m³.

A következő táblázat km-ben és a központi égitest sugarában (R) adja meg a Roche-határ értékeiket. A pontos Roche-határ függ a keringő égitest sűrűségétől és szilárdságától.


központi égitest	keringő égitest	Roche-határ (szilárd)		Roche-határ (folyékony)
központi égitest	keringő égitest	távolság (km)	R	távolság (km)	R
Föld	Hold	9496	1,49	18261	2,86
Föld	átlagos üstökös	17880	2,80	34390	5,39
Nap	Föld	554400	0,80	1066300	1,53
Nap	Jupiter	890700	1,28	1713000	2,46
Nap	Hold	655300	0,94	1260300	1,81
Nap	átlagos üstökös	1234000	1,78	2374000	3,42

Ha a központi égitest sűrűsége kevesebb mint fele a keringő égitestének, akkor a szilárd Roche-határ kisebb, mint a központi égitest sugara, és a két égitest hamarabb ütközne, mint hogy a szatellita a Roche-határhoz érne.

Milyen közel vannak a Naprendszer holdjai a Roche-határaikhoz? Az alábbi táblázatban belső holdak pályasugarának és Roche-határának aránya szerepel. A Pan és a Naiad különösen közel van a szétesést jelentő zónához. Az óriásbolygók belső holdjainak sűrűsége pontosan nem ismert, ezeknél a feltüntetett értékek csak becslések (dőlt betűkkel).


központi égitest	keringő égitest	pályasugár : Roche-határ
központi égitest	keringő égitest	(szilárd)	(folyékony)
Nap	Merkúr	104:1	54:1
Föld	Hold	41:1	21:1
Mars	Phobos	172%	89%
Mars	Deimos	451%	234%
Jupiter	Metis	~186%	~94%
	Adrastea	~188%	~95%
	Amalthea	175%	88%
	Thebe	254%	128%
Szaturnusz	Pan	142%	70%
	Atlas	156%	78%
	Prometheus	162%	80%
	Pandora	167%	83%
	Epimetheus	200%	99%
	Janus	195%	97%
Uránusz	Cordelia	~154%	~79%
	Ophelia	~166%	~86%
	Bianca	~183%	~94%
	Cressida	~191%	~98%
	Desdemona	~194%	~100%
	Juliet	~199%	~102%
Neptunusz	Naiad	~139%	~72%
	Thalassa	~145%	~75%
	Despina	~152%	~78%
	Galatea	153%	79%
	Larissa	~218%	~113%
Plútó	Charon	12,5:1	6,5:1

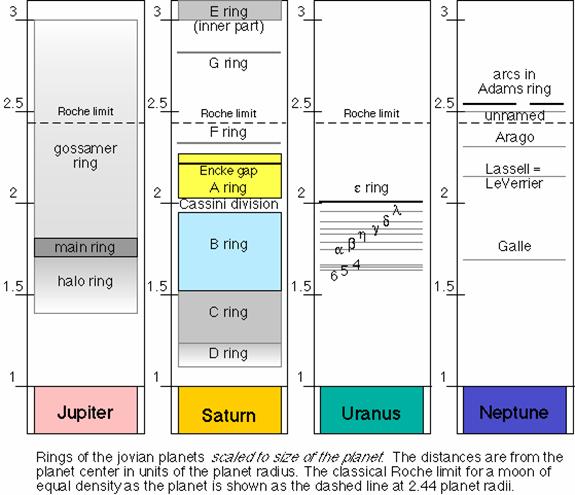
A Wikipédia és más források alapján készítette: Dr. Szatmáry Károly, Szegedi Tudományegyetem