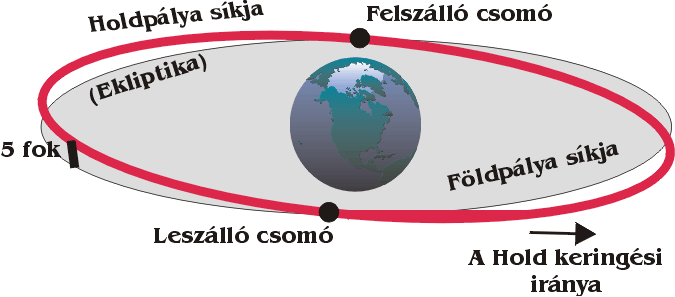
A HOLD MOZGÁSA

  ÁLTALÁNOS LEÍRÁS, A HOLDPÁLYA VÁLTOZÁSAI

Fontosabb adatok (Almár-Horváth, 1981; Marik, 1989; Both, 2000)

Rotációs periódus = 27,321 661 4 nap
Sziderikus keringésidő (a csillagokhoz képest) = 27,321 661 4 nap
Szinodikus keringésidő (két azonos fázis közti időtartam) = 29,530 588 7 nap
Drakonikus hónap (két, felszálló csomón való áthaladás közti idő) = 27,212 220 4 nap
Anomalisztikus hónap (két perigeumátmenet közötti időkülönbség) = 27,554 550 9 nap
Átlagos pályamenti sebesség = 1,025 km/s
Az egyenlítői sík hajlásszöge a pályasíkhoz = 6,°68
Legkisebb földtávolság (perigeum) = 356 000 km
Legnagyobb földtávolság (apogeum) = 407 000 km
Közepes földtávolság 60,268 Föld-sugár = 384 400 km
A holdpálya közepes excentricitása = 0,054 9
A pályasík hajlásszöge az ekliptikához (inklináció) = 5,°145

A Hold keringő mozgása. A legegyszerűbb modell szerint eljárva, a Holdat és a Földet egyaránt gömbszimmetrikus testnek tekinthetjük, amelyek elipszispályájukon keringengenek a közös tömegközéppont körül (ez természetesen a Föld belsejében van). Ha külső hatás sem lenne, szabályos Kepler-féle mozgást végeznének; az utolsó három adat lenne a megfelelő három pályaelem.

A valóságban azonban közelsége miatt a Hold jobban „érzi"a Föld belsejében meglévő tömegeloszlás-egyenetlenségeket is. Ez esetben tehát bolygónkat nem tekinthetjük gömbszimmetrikusnak, ami a számolást pedig jócskán megkönnyítené, hiszen ekkor a Földet egyszerűen tömegponttal helyettesíthetnénk. Nem hanygolhatjuk el a többi égitest zavaró hatását sem. A legfontosabb a Nap, amely különösen nagy perturbációkat okoz. A bolygók közvetlenül is hatnak a Holdra, de a Földre is, s ezáltal közvetlen és közvetett perturbációkat egyaránt keltenek. A Hold összesen többszáz féle mozgást végez. Ráadásul, mivel igen közel van, a mozgása nagy pontossággal megfigyelhető, s hasonló pontossággal kellene azt matematikailag is visszaadni. Ilyen bonyolult mozgásnál pedig ez nagyon nehéz feladat.

5. ábra. A Hold pályája (ELTE Csill. Tanszék honlap)

Valójában a holdpálya mind a 6 pályaeleme ( az a fél nagytengely, a lapultságot kifejező e numerikus excentricitás, az i inklináció, az W felszálló csomóhossz, az w perigeum argumentum és az M₀ középanomália) változik, és viszonylag gyorsan.

Ezek közül a W és w mért változásai 100 év alatt:
 

	Dw	DW
Fő szoláris perturbáció	+14 642 722",8	-6 967 206",9
Korrekciók ehhez	-71,3	+20,3
Bolygók közvetlenül	+269,0	-142,0
Bolygók közvetve	-16,1	+5,0
Föld alakjától	+633,1	-592,1
Relativisztikus korrekció	+0,06
Összesen	+14 643 537",6	-6 967 915",7

(Az adatokat idézi Marik, 1989.)

A holdpálya perigeuma a Nap okozta legfontosabb perturbáció eredményeképpen 8,850 339 év alatt a keringéssel egyező irányban körülfordul, ezt a mozgást azonban még más, szabályosan ismétlődő hatások is megzavarják. A legnagyobb ilyen háborgás amplitudója 8^o41’. A pálya excentricitása - alakja - is változik, kis kitéréseket végez a középérték körül.

A felszálló csomó ellentétes irányban, 18,599 49 éves periódusidővel körbeforog, amelyet szintén „meghullámosítanak" más periodikus perturbációk; közülük a legnagyobb 1^o26’. Az inklinációs szög pedig közben 4^o57’ és 5^o20’ között ingadozik.

A szabályosan ismétlődő perturbációk közül a legfontosabbaknak saját neve is van; ezek a Hold w valódi ekliptikai hosszúságában (Érdi, a Marik, 1989 könyvben):

w = l + 377’sinM + 13’sin 2M + … +
+ 76’sin (2h - 2h₁ - M) + … +
+ 39’sin 2(h - h₁) - … - 11’sinM₁ - … -
- 2’sin (h - h₁) + …

A Hold mozgásának leírásához mindezeket a hatásokat figyelembe kell venni, le kell vezetni. Az első, igen pontos elméletet E. W. Brown vezette le a századforduló idején. Az általa készített táblázatokban a Hold koordinátáit négyváltozós Fourier-sorokkal számítják:

w = l+S w_n sin f_n

ß = S ß_n sin f_n

sin p_H = S c_ncos f_n ,

ahol w, ß, és p_H a Hold ekliptika menti valódi hosszúsága, szélessége és parallaxisa,
w_n , ß_n , c_n a táblázatok megadta számok, la Hold a periodikus háborgások nélküli közepes pályamenti hosszúsága,

f_n = k₁ D + k₂ l + k₃ l₁ + k₄ F.

Az itt szereplő k₁, k₂, k₃ és k₄ egész számok; D, l, l₁, F az ún. Delaunay-alapargumentumok.Ezen változók értékei:

l= 17 325 594",060 85 t + 270^o26’11",71
l = l - o = 17 179 167",085 94 t + 296^o6’25",31
l₁ = h₁ - o₁ = 1 295 977",415 16 t + 358^o28’33",00
D = l- h₁ = 16 029 616",645 69 t + 350^o44’23",67
F = l- O = 17 395 266",093 19 t + 11^o15’11",92

Itt o és O a Hold perigeumának és felszálló csomójának hosszúságai a periodikus zavarások nélkül, az 1 index-szel jelölt mennyiségek a Nap látszólagos pályájára vonatkoznak, t pedig az 1900-tól eltelt időt jelenti, Julián-években.
A különféle változók más-más periódusnak felelnek meg. Így l periódusa a sziderikus (27^d,321 661 4 + 0^d,000 000 2 t_c), l-é az anomalisztikus (27^d,554 550 9 - 0^d,000 001 t_c), D-é a szinodikus (29^d,530 588 7 + 0^d,000 000 2 t_c), míg F-é a drakonikus (27^d,212 220 4 + 0^d,000 000 4 t_c) holdhónap. t_c az 1900,0-tól Julián Évszázadban eltelt idő. A táblázatok a w_n és ß_n együtthatókat 0",001-es, a c_n-eket pedig 0",000 1-es pontossággal adták meg.

A Brown-féle eljárást később még többször tökéletesítették, pl. mikor kiderült, hogy a Föld nem egyenletesen forog a tengelye körül, a világidőről áttértek az ún. efemerisz időre (ez szerepel a bolygók mozgását a gravitációs elv alapján leíró egyenletekben is). Manapság azonban már a többszörösen javított Brown-elmélet sem kielégítő pontosságú.

Többen is próbálkoztak a perturbációk pontosabb meghatározásával. Így a Nap keltette háborgásokat többek között M. C. Gutzwiller és D. S. Schmidt vizsgálta. Nagy teljesítményű számítógépek segítségével 0",000 01-es belső pontosságot értek el. A planetáris eredetűek közül D. Standaert 1982-re a Mars és a Vénusz összes elsőrendű és néhány másodrendű, J. Chapront és M. Chapront-Touzé ugyanerre az évre minden bolygó elsőrendű közvetett és közvetlen perturbációját kiszámította. A kívánt pontossághoz azonban a perturbációkat másodrendben is ki kell számolni, ami azért nehéz, mert ilyenkor az azokat megadó sorok már nagyon sok tagból állnak.

A Föld és a Hold egyenetlen tömegeloszlásából származó hatásokkal J. Henrard foglalkozott. Az előbbi esetben 0",000 01-es nagyságrendű pontosságot ért el. A Holdban lévő tömegeloszlás-inhomogenitás csak 0",000 24-es eltéréseket okozhat. A fellépő relativisztikus perturbációkatV. A. Brumberg számította. Ezek közül a pálya menti hosszúságban fellépő fellépő legnagyobb értéke -0",000 55 sin 2D-nek adódott (Érdi, a Marik, 1989 könyvben).

Egyéb mozgások. Rezgés. A pontosabb (lézerrel végzett) mérések tanúsága szerint a Hold harangszerű rezgést végez, amely egy állítólagos középkori nagy becsapódás utózöngéje lehet. Tengely körüli forgás. A forgási periódus megegyezik a (sziderikus) keringésidővel, ezért a Hold mindig ugyanazt az oldalát mutatja a Föld felé. A tengelyforgása viszonylag egyenletes, azt ugyanis a Földi árapályerők állították be így. Ez esetben tehát a Föld hatása igen csekély lehet, s inkább csak a keringési sebesség egyenetlenségeinek köszönhetően áll elő. A planetáris és szoláris perturbációk hatása nagyobb lehet.

 A HOLD LÁTSZÓLAGOS ÉGI MOZGÁSA, FÁZISOK

Napi változások. A Hold keringési és a Föld forgási iránya megegyezik, de a Hold lassabb, periódusideje több, mint 27-szerese a Földének. Ezért a Hold a minden nap kb. 50 perccel később és később kel fel. A Föld forgása közben ui. ő is elmozdul, s bolygónknak 24 óra (1 nap) elteltével még 50 percre van szüksége ,hogy „utolérje" a Holdat, s az felbukkanjon a látóhatár felett. Az ún. lunadikus nap időtartama tehát 24 óra 50 perc.

Fázisok. Hogy a holdkorong hányad részét látjuk éppen, az a Föld, a Hold és a Nap egymáshoz viszonyított helyzetétől függ. Újhold idején a Hold a Földet és a Napot összekötő egyenes mentén, a két égitest között helyezkedik el. Mivel az éjszakai oldalát fordítja felénk, ilyenkor többnyire nem is látszik az égen. 2-3 nap múlva már egy keskeny, de növekvő holdsarlót látunk. Kb. 1 héttel újhold után következik az elsőnegyed, mikor a Hold és a Nap iránya a Földről nézve derékszöget zár be. Ilyenkor az égen a növő félhold jelenik meg, napnyugtakor emelkedik legmagasabbra, majd éjféltájban lenyugszik. A telihold 14-15 nappal az újhold után van, ekkor a Nap, a Föld és a Hold egy egyenesbe esnek, ebben a sorrendben. Ekkor a teljes holdkorongot megfigyelhetjük, amely egész éjjel az égen van. Fényessége ekkor a legnagyobb, -12,5 rendű (a Napé -26,7 rendű), a csillagok fényereje természetesen sokkal kisebb (Hédervári, 1962). Ezután fogyni kezd, újabb egy hét múlva érkezik a harmadik negyedbe, amely tükörképe az elsőnek; ekkor éjfél körül kel, és napkeltekor delel. Végül, 2-3 nappal újhold előtt még látható, az ezután következő 4-5 napban már nem, majd az egész kezdődik előlről.

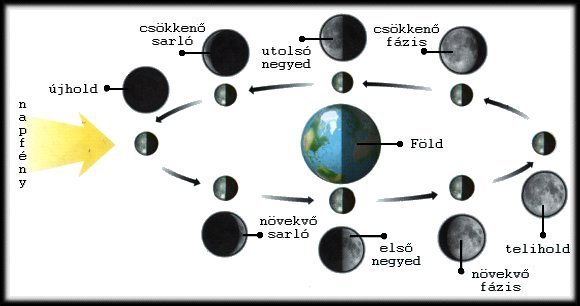
Egy teljes periódus időtartama, a szinodikus keringésidő, kb. 29 és fél nap. Azért hosszabb az ún. sziderikus keringésidőnél, melyet az állócsillagokhoz képest mérünk, mert a Hold keringése közben a Föld 28^o-kal továbbhalad Nap körüli pályáján. Így a Nap ugyanennyivel kerül arrébb az ekliptikán, s a Holdnak, hogy ismét a Nap-Föld egyenesre kerüljön (újhold legyen), még két nap továbbkeringésre van szüksége (Herrmann, 1992).

Évi változások. A Hold télen magasabban, míg nyáron alacsonyabban látható a Föld egén. Ennek oka az, hogy a Hold pályasíkja csaknem az ekliptika (a Nap látszólagos évi pályája) síkjában van. Telihold idején a 3 égitest jó közelítéssel egy egyenesbe esik, ha tehát a Nap magasan áll, vagyis nyár van, akkor a túloldali Holdnak alacsonyan kell lennie és fordítva. ( Könnyen ellenőrizhető, hogy a Föld mindkét féltekéjén ez a helyzet.)

Librációk. A földi szemlélő a Holdat égi mozgása közben enyhén „billegni" látja. Ezeket az ingadozásokat gyűjtőnéven librációknak nevezzük. Nélkülük a holdfelszínnek csak pontosan a felét láthatnánk, igy viszont a perem mentén a túlsó oldal egy kis részét is megfigyelhetjük. A librációknak két alaptípusa ismert.

Optikai librációk.

1. Szélességi libráció. Alapja az, hogy a Hold pályája valójában nem esik az ekliptika síkjába, hanem azzal kb. 5 ^o-os szöget zár be. Ezért hol e sík fölött, hol alatta látjuk egy kicsivel. Az előbbi esetben a déli, az utóbbiban az északi sarok mögé láthatunk, mindkét esetben 7 ^o-kal a szélességi körök mentén.
2. Hosszúsági libráció. A Hold keringési és forgási periódusideje ugyan megegyezik, de közülük csak a forgása egyenletes. Mivel a pályája nem kör, hanem ellipszis, a haladási sebessége is a Kepler-féle törvényeknek megfelelően ingadozik. Ezért, amikor földtávolban lelassul, a Hold kissé "túlforog", mikor földközelben felgyorsít, a forgása lemarad, így mindkétszer meglátunk valamennyit - 7,9 ^o-ot - a nyugati, illetve keleti szélek mentén a túloldalából (Marik, 1989).
3. Napi (parallaktikus) libráció. A felkelő és a lenyugvó Holdat más szögből látjuk, hiszen addigra jelentősen elmozdult az égen. Az előbbi esetben a nyugati, az utóbbiban a keleti peremén látunk túl, igaz, mindkétszer csak 40 szögpercnyire.

Fizikai libráció. Ez nem látszólagos, hanem valódi mozgása a Holdnak. Ő ugyanis egy igen kismérvű, rezgő vagy ingadozó mozgást is végez egy egyensúlyi állapot körül. A Föld-Hold rendszer közös tömegközéppontját összekötve a Hold középpontjával, észrevehető, hogy mozgás közben hol a keleti, hol a nyugati széle mozdul efelé az egyenes felé. Így is megfigyelhetünk a nyugati szegélye mentén valamennyit a túloldalból, bár ez legfeljebb 0,5 szögmásodperc lehet (Hédervári, 1962).

A librációknak köszönhetően a holdfelszín összességében 59%-át láthatjuk közvetlenül a Földről. De más hasznukat is vehetjük: többek között a fizikai librációk mérésével sikerült következtetni a holdmag méretére.

 FOGYATKOZÁSOK

Napfogyatkozás újholdkor lehetséges, mikor a Hold a Föld és a Nap közé kerül, és bolygónkról nézve eltakarja a csillagot. Három fajtája van.

1. Részleges. Ilyenkor a holdkorong csak részben fedi el a Napot, a földi megfigylő a Hold félárnyékában tartózkodik.

2. Teljes, ha az egész Nap eltűnik egy időre, vagyis a teljes árnyékba kerülünk. Ekkor rendszerint elég sötét lesz ahhoz, hogy a csillagok nagy része láthatóvá váljék. A Hold a földfelszínnek csupán kis, legfeljebb 200 km átmérőjű részét árnyékolhatja be teljesen, mivel a teljesárnyék-kúpja ebben a távolságban már igen keskeny. A két bolygó együttes mozgása ezt a kis, kör alakú árnyékfoltot nagy sebességgel, az egyenlítőhöz viszonyítva 336 km/h-val mozgatja végig a Föld felületén. Azt a K-Ny-i irányú sávot, amin végighalad, totalitási zónának nevezzük, a teljes fogyatkozás csak innen látható. Egy adott helyen a teljes takarás legfeljebb 8 percig tart.

3. Gyűrűs napfogyatkozás akkor fordul elő, ha a Hold éppen apogeumában tartózkodik. Ilyenkor már olyan kicsinek látszik a Földről, hogy nem tudja teljesen eltakarni a napkorongot, így annak külső gyűrűje még látszani fog. Ez a legritkább a három közül.

Holdfogyatkozás ellenkezőleg, teliholdkor van. Ekkor a Föld kerül a Hold elé, s nálánál jóval nagyobb átmérőjű árnyékkúpjával részben vagy teljesen eltakarja. A napfogyatkozással ellentétben ezt a Föld nagy területéről lehet látni; az éjszakai félgömbön mindenhonnan, ahol a Hold látszik az égen. Mivel a teljes holdfogyatkozás időtartama elég hosszú (maximum 3,5 óra lehet), s ennyi idő alatt a Föld jelentősebben elfordul, a teljes területének több, mint feléről látható a jelenség. A Hold azonban rendszerint nem tűnik el teljesen a Föld árnyékában. Általában sötétvöröses színbe burkolózik, mivel a közvetlenül az árnyékkúp mellett elhaladó fénysugarakat a Föld légkörének fénytörése befelé, a sötétbe téríti, s közülük a leghosszabb hullámú vörös nyelődik el a legkevésbé. Mindez azonban a fény szóródás miatt függ a légkör állapotától, sőt, a portartalomtól is.

Tudjuk, hogy a Hold felszálló csomója mintegy 18,6 éves periódusidővel, a keringéssel ellentétes irányban forog (3.1.1. fejezet). Ennek következtében a fogyatkozások időpontjai is minden évben kissé korábban következnek, de egy-egy fordulat végén ez a ciklus is előlről kezdődik. Ez az ún. Szárosz-féle ciklus, ami azonban mai számítások szerint néhány ezer év múlva megszűnik (Herrmann, 1992).

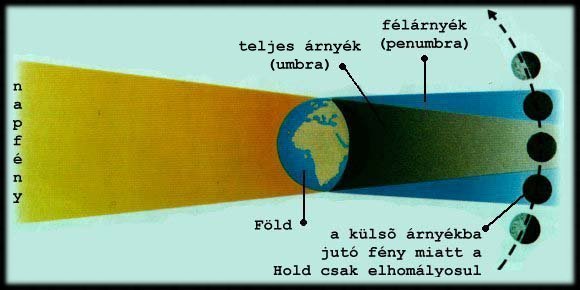
7. ábra. A holdfogyatkozás

Fogyatkozás azonban nincs minden új- és telihold idején. A Hold keringési síkja ugyanis több, mint öt fokos szöget zár be a Föld Nap körüli keringési síkjával (vagyis az ekliptikával), s mivel a megvilágítás a Nap felől érkezik, a két bolygó árnyékkúpja többnyire elkerüli a másikuk felszínét. A holdpálya két pontban metszi az ekliptikát (ezek az ún. csomópontok), s fogyatkozás akkor lehetséges, mikor a Hold egyikük közelében tartózkodik és a megfelelő fázisban (új- vagy teliholdban) van. Ez a két követelmény pedig ritkán teljesül egyszerre, kb. félévenként, de akkor több is előfordulhat (évente átlagosan 1,5 hold- és 2,3 napfogyatkozás figyelhető meg).

 AZ ÁRAPÁLY-JELENSÉG

Az alapvető fizikai ok a gravitációs mező természetében keresendő. Mivel ez az erő fordítva arányos a két tömeg távolságának négyzetével, ezért a próbatestnek a másikhoz közelebbi tömegpontjaira nagyobb erő hat, mint a távolabbiakra. Az egyszerűség kedvéért vegyünk két tömegpontot, m₁-et és m₂-t, amit egy r hosszúságú, merev, súlytalannak képzelt rúd köt össze. Ezt helyezzük egy M tömegű égitest közelébe, oly módon, hogy az r szakasz beleessen a M tömegközéppontjától az m₁-m₂ rendszer tömegközéppontjáig húzott egyenesbe. A közelebbi m₁ test R távolságra van a M tömegközéppontjától. Ekkor a két próbatestre ható erőkülönbség:

F_k = G m₁ M/R² - G m₂ M/(R+r)² = G M [ m₁/R²- m₂/(R+r)²]

Ezt a különbözetet hívjuk gravitációs árapályerőnek. Mivel pl. m₁ = m₂ esetén a közelebbi tömegpontot nagyobb erő húzza, a különbség tulajdonképpen szét akarja szedni a rendszert. Az árapályerő a távolság négyzetével fordítva, az okozó test tömegével egyenesen arányos.

Mivel az égitesteknél is érvényesül, hogy a közelebbi oldalt összességében nagy erő húzza, mint a távolabbit, ezért a nagyobb méretűek jellegzetes „rögbilabda" alakúvá torzulnak. A bolygók és holdjaik esetében a fenti alakváltozás általában jelentéktelen, de az anyabolygóhoz közelítve egyre nő, majd a Roche-féle határt elérve az erőkülönbség leemeli a hold felszínét, azután sorra a kövekező rétegeket. Ezeket is feldarabolná, míg csak apró kövek maradnának, olyan mérettel, amelynél az erőkülönbözet nem elég nagy a további aprózódáshoz. Az óriásbolygók Roche-zónájában lévő anyagok nagyobb része nem is tudott holdakká összetömörödni, hatalmas gyűrűrendszerekként keringenek körülöttük. Érdekes, hogy azért ez a szabály sem feltétlenül érvényes mindenkire, a veszélyes övezeten belül is találhatunk holdakat ( ezek az ún. „terelőholdak"), az ő egybentartásukban azonban a gravitációs erőn kívül más természetű, pl. atomi erők is részt vesznek.

 TENGERI ÉS SZILÁRD DAGÁLYOK A FÖLDÖN ÉS A HOLDON

Az árapályhatás legismertebb következménye a földi tengerjárás. Ennek két oka van.

Az első az előbb említett árapályerő: a Hold a Föld tömegközéppontjára egy átlagerővel hat, ám a közvetlenül alatta lévő víztömeget erősebben vonzza, - az meg is emelkedik felé -, míg a túloldali vízréteget gyengébben, tőle tehát magát a Földet húzza el.

A második a Föld és a Hold egymás körüli keringése (lásd a 8. ábrát). Ha R a Föld sugara, a két égitest tömegközéppontja - S - a Föld O tömegközéppontjától r₁ = 3R/4 távol van. A Hold és a Föld is tulajdonképpen egy síkban, e pont körül keringenek a Hold sziderikus keringésidejével mint periódusidővel. A forgó rendszerekben a centrifugális erő is fellép, az ábrán -a_tr gyorsulást hozva létre. Ha a Föld forgásától eltekintünk, ez bármely tetszőleges p pontjában ugyanannyi lesz.

a_tr = G m_H /r²

a p pontban a gravitációs gyorsulás:

a_gr = G m_H /r_p².

Mivel a Föld középpontjában r = r_p , ezért a két erő eredője itt 0 lesz, máshol azonban ettől különbözik. Az ábra alsó felén az eredő erő F_t érintőirányú komponense kelti az árapályt. Az ábrán ezt több pontban meg is szerkesztették. A víztükör mindig merőlegesen igyekszik beállni a rá ható eredő erőre (ha a felszín még nem merőleges, az erőnek lesz rá ható vízszintes komponense is, ami a rétegeket addig csúsztatja el egymáson, míg az nem lesz), ezért a rajznak megfelelően A és B pontokban egy-egy dagálypúp keletkezik, míg C-ben és B-ben csökken a vízszint, vagyis ott apály alakul ki. Végeredményben, a Föld alakja kissé hupli formájúvá torzul. Természetesen ez igen kicsi változást jelent (Budó,1992).

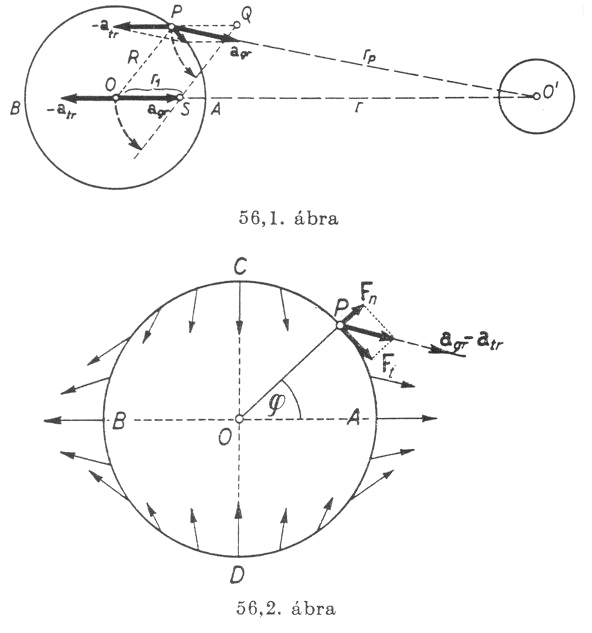
8. ábra. A Hold keltette árapály (Budó, 1992)

De nem csak a Hold, hanem a Nap is kelt árapályt, bár az a Holdénak csak az egyharmadáig emelkedik (Comins, 1994). A dagálypúp akkor a legmagasabb (szökőár), ha a Nap és a Hold a Földdel egy egyenesbe esnek, - vagyis újhold és holdtölte idején - mivel ilyenkor egymás hatását erősítik. Ilyenkor az apály is alacsonyabb az átlagosnál. Amikor pedig a legjobban lerontják, (az első és harmadik negyedben, mikor a Nap és a Hold a Földről nézve derékszöget zárnak be egymással), akkor a legalacsonyabb, ezt hívjuk vakárnak. Ekkor az apály is magasabb lesz. A köztes időszakokban a helyzet sokkal bonyolultabb; előfordul, hogy a holdjáráshoz képest órákkal lemarad a dagály a Nap hatására.

A jelenség azonban nem ilyen egyszerű. Az apály és a dagály ugyan naponta kétszer ismétlődik, ám ez a lunadikus nap szerint történik, amely 24 óra 50 perces. A Hold távolsága is változik a perigeum és apogeum között, s mivel a dagályhullám magassága a távolság köbével fordítva arányos, ez is viszonylag jelentős eltérést okozhat. A Hold deklinációjától (az égi egyenlítőtől mért szögtávolságától) is függ, mivel ha ez nagy, a dagályok is aszimmetrikussá válnak.

A dagály magassága a tengeraljazat szerkezetével is változik, pl. szűk öbölbe vagy folyótorkolatba behatolva, a víz feltorlódik, s nagy dagály keletkezik. Az időjárás is befolyásolja, pl. alacsony légnyomáson vagy erős szélben is nőhet a dagályok magassága (Both, 2000).

Nemcsak a tengerek, de a földkéreg is elmozdul ily módon. Ez az ún. szilárd tengerjárás. Igaz, még a közvetlenül a Hold alatt lévő kőzetrétegek is csak néhány cm-t mozdulnak felfelé, de ennek a jelenségnek komoly jelentősége lehetett a múltban (mikor a Hold még sokkal közelebb volt), s esetleg a jelenben is. (Ennek következményeiről szól egy későbbi fejezet.)

Az árapályerő hatása a légkörben is érződik: áramlások indulhatnak meg. Ezek az alsó atmoszférában még jelentéktelenek az időjárás okozta légmozgásokhoz képest, de 100 km-es nagyságrendű magasságokban már jelentős cirkulációkat okozhatnak. Ezért az árapályhatás közvetlenebbül is hatással van a földi éghajlatra, ez azonban igen finom és részleteiben még csak kevéssé ismert folyamat.

A Holdon - víz hiányában - csak a szilárd tengerjárások léteznek, de ezek erőteljesebbek, mint nálunk, hiszen a Föld tömege jóval nagyobb, mint a Holdé (kb. 81-szer akkora). Az ő felszíne mégsem emelkedik jobban felfelé, mert a szilárd litoszféra ott túl vastag. Ennek ellenére vannak bizonyos geológiai következményei a holdi szilárd tengerjárásnak, (lásd az 1.2.1.fejezetet). Látványosabb következmény a Hold kötött forgása, amely szintén a földi árapályerőnek köszönhető. Az idők során a Föld a Hold forgását „beállította", így annak rotációs periódusa megegyezik a (sziderikus) keringésidejével. (Ebből adódik, hogy a Hold mindig ugyanazt az oldalát fordítja a Föld felé.)

KÖVETKEZMÉNYEK

 A Föld forgástengely-stabilitása

A Föld forgása az idők során sokat változott, beleértve nemcsak a sebességet, de a forgástengelyt is. A bolygó, akár egy hatalmas pörgettyű, igyekszik megtartani a tengely irányát, de a külső erőhatások azt mégis befolyásolják.

Mint az előbbiekben (3.1.1. fejezet) már volt szó róla, a Föld nem gömbszimmetrikus égitest, hanem ún. forgási ellipszoid. A centrifugális erő hatására az Egyenlítő mentén nagyobb az átmérője, mint a sarkoknál. Igaz, a lapultság mértéke mindössze 1/298 (Herrmann, 1992). Az Egyenlítő 23,5^o-os szöget zár be a földpályával, tehát a Föld itteni kitüremkedése nem a Nap és nem is a Hold felé mutat. (Mivel a holdpálya 5,1^o-kal tér el az ekliptikától, az egyenlítővel bezárt szöge 23,5^o + 5,1^o , vagyis 18,4^o és 28,6^o között változik.) Erre a két kidudorodásra ezért mindketten forgatónyomatékot fejtenek ki, amely a forgástengelyt a saját irányukra merőleges szögbe igyekszik beállítani. Kettejük közül a közelebbi Hold hatása nagyobb.

Mindez azért fontos, mert újabb vizsgálatok (Sky and Telescope, 1998) arra mutatnak, hogy valójában a Hold tartja stabilan a forgástengelyt, állandóan a merőleges felé fordítva, s így megfékezi az attól túlságosan eltérítő mozgásokat is. Ezért a földtengely csak egy 2 × 23,5^o = 47^o nyílásszögű kúppalást mentén tud precesszálni az ekliptikára merőleges egyenes körül, mintegy 25 700 éves periódusidővel (ez az ún. Plátói év). Mivel ez az Egyenlítő, és természetesen a neki megfelelő égi egyenlítő (equator) elfordulásával jár, a Tavaszpont is eltolódik, s így az égi vonatkoztatási rendszer is megváltozik; azt tehát bizonyos időközönként újra ki kell jelölni, s hasonlóan pl. a Sarkcsillagot is.

A precesszió kúppalástjának hullámosságát nutációnak nevezzük. Ez azért jelentkezik, mert a Hold hatása is ingadozik. Minimális, mikor a Hold maximális szögtávolsága az Egyenlítőtől a legkisebb, és maximális, mikor a legnagyobb (vagyis mikor a holdpálya felszálló csomója a Tavaszpontban van, ekkor a fentiek szerint 28,6^o). Következéskképpen a nutációs periódusidő megegyezik a holdpálya csomóvonalának 18,6 éves körülfordulási idejével.

Ha a Hold nem létezne, a földtengely hajlása kaotikusan változna; 0^o-tól 85^o-ig bármilyen értéket felvehetne, ami a földi éghajlatra igen súlyos következményekkel járna (lásd később).

 A rendszer perdület-átrendeződése: a Föld lassuló forgása, a Hold távolodása

Ez az árapály-jelenség egy egészen sajátos következménye (Comins, 1994). A Hold a Föld forgásával egyező irányban kering, de jóval lassabban: bolygónk több, mint 27-szer megfordul a tengelye körül, míg kísérője egyszer megkerüli. A Hold által felemelt víztömegek is csak az ő sebességével mozognak körbe a Földön, s közben utolérik őket a kontinensek, amelyeknek nekiütődnek, s a szintén gyorsabban mozgó tengeraljzattal is súrlódnak. Mindez kissé fékezni igyekszik a Föld forgását.

Ha a Földet tökéletesen gömbszimmetrikus felépítésű égitestnek képzeljük, a Holdra gyakorolt gravitációs erő szempontjából tömegponttal helyettesíthetjük. A - Hold keltette - két dagálypúp azonban elrontja a dolgot; mivel a bolygó közel van, a dagályok tömegvonzását sem lehet elhanyagolni. A Föld gyorsabb forgása - szintén a súrlódás közvetítésével - magával ragadja kissé a dagályhullámokat, ezért azok nem a Hold alatt helyezkednek el: az innenső oldali mindig kissé előrébb, a túloldali pedig kissé hátrább jár a Holdhoz képest. Így a Föld, a dagálypúpok és a Hold tömegközéppontjai nem esnek egy egyenesbe, s a dagályok által a Holdra kifejtett vonzóerőnek lesz a holdpálya érintője irányába eső komponense is. Az innenső oldali, tehát közelebbi dagálypúp előresietve gyorsítani, a túloldali, távolabbi pedig hátramaradva lassítani akarja a Holdat földkörüli keringésében. Természetesen a közelebbi víztömeg tömegvonzása a nagyobb, az eredő erő tehát növeli a bolygó sebességét. Így az az égimechanika törvényei szerint állandóan magasabb pályára kerül, s csavarvonalban távolodik a Földtől. ( A valóságban a Földet nem tekinthejük gömbszimmetrikusnak. A dagályok tömegközéppontja helyett pedig a hupli alakúra deformálódott Föld integrált gravitációs erejével kellene számolnunk. Az eredmény azonban az egyszerűsítések ellenére hasonló lenne.)

Végeredményben a Föld forgási perdülete a Hold keringési perdületévé fog átalakulni, érvényesítve az ismert megmaradási elvet. Nyilvánvaló, hogy ez nagyon lassú folyamat, amelynek számottevő eredménye csak évmilliók alatt jelentkezhet.

1. Feladat: számítsuk ki a Hold-Föld távolság alakulását az idő függvényében, s ebből a Hold távolodási sebességét, bizonyos egyszerűsítésekkel. Ezek a következők:

1. A Hold a Földet szabályos körpályán kerüli meg, a földi egyenlítő síkjában;
2. Eltekintünk az összes többi égitest hatásától;
3. A Földet gömbszimmerikus égitestnek tekintjük;
4. A földi kontinensek hatását is elhanyagoljuk.

(1) dN(t)/dt = M(t) , ahol N(t) a perdület, M(t) pedig a forgatónyomaték.

A Hold keringési perdülete:  (2)   N_H(t) = m_H r²(t) w_H(t) ,

(3)   m_H w_H²(t) r(t) = G m_H m_F/r²(t) , ahol G a gravitációs állandó, m_F a Föld tömege. Innen,

 ha kifejezzük w_H(t)-t és behelyettesítjük a (2) egyenletbe:
                            ____    ___
(4)  N_H(t) = m_H \/ G m_F \/ r(t)

Ezt differenciálva (1) így alakul:
                 _____                  ___
(5) m_H/2 \/ G m_F dr(t)/dt 1/ \/ r(t) = M [r(t),t].

Ezt az elsőfokú differenciálegyenletet megoldva kaphatjuk a keresett r(t) mennyiséget, azt idő szerint visszaderiválva pedig a Hold távolodási sebességét. Ha a jobboldal csak t-től függ, az egyenlet szeparálható. Az igazi probléma természetesen az M[r(t),t] mennyiség kiszámítása. Ez a Földnek a Holdra gyakorolt gyorsító forgatónyomatéka, amely nagyságában megegyezik, irányában ellentétes a Hold Földre gyakorolt fékező forgatónyomatékával.

A valóságban természetesen az egész folyamat jóval bonyolultabb. Legalább két dolog van, ami a fenti számítást formálissá teszi. Az egyik a Nap hasonló fékező hatása, amely kisebb ugyan a Holdénál, ám elhanyagolni mégsem lehet. A másik kontinensek léte. Ezek nagyban erősítik az árapály fékező nyomatékát, mivel egyrészt a beléjük ütköző dagályhullámok majdnem teljes lendületüket átadják nekik, másrészt a kontinentális talapzatokon (selfeken) a tengerfenék közelebb van a felszínhez, tehát erősebb a súrlódás. Mikor a dagályhullám a tengeraljzattal dörzsölődve fékezi a Földet, csak a súrlódás következtében teszi, és a lendületváltozás is kisebb. Mivel a dagály az Egyenlítő mentén a legmagasabb (itt van legközelebb a Hold), nem mindegy, hogyan helyezkednek el a különböző szárazulatok a Földön. Mikor több a földrész az Egyenlítőnél vagy a közelében, jobban lassul a Föld. A kontinensek fékező hatását tehát csak akkor lehetne figyelembe venni, ha le tudnánk írni a pontos mozgásukat az idők során. Jelenleg a geológusok kb. 1,5 milliárd évre visszamenőleg ismerik a kontinensvándorlást. Ezért a földforgás változásainak leírására inkább empírikus összefüggéseket használunk. A kutatás több irányban is folyik a lassulás múltbeli és jövőbeli lefolyásának meghatározására.

Üledékes kőzetek vizsgálata. A Charles P. Sonett és Erik P. Kvale vezette kutatócsoportok megpróbálták kiszámítani az árapály-periódusok időtartamát, többek között a Salt Lake City közelében talált üledékes kőzetekből. Ezek rétegesen rakódtak egymásra, s azok az élőlények (pl. korallok, stromatolitok), amelyek vázából keletkeztek, napi, havi és évi növekedési ritmust is mutattak. Ezek összehasonlításából ki lehet következtetni, hány napig tartott egy év akkoriban. Ha a Föld pályamagassága nem változott azóta, akkor 900 millió évvel ezelőtt (ennyi az említett kőzetek kora) a Hold sziderikus keringésideje 23,4 (mai) nap volt, egy (akkori) nap viszont csak 18 óráig tartott. A Hold-Föld távolság pedig a mainak 90%-a lehetett (Sky and Telescope, 1997/1).

Csillagászati megfigyelések alapján. Az így nyert adatok, valamint a Hold távolságának pontos, lézeres kimérésével (felhasználva az Apolló-űrhajók által otthagyott különleges tükröket) arra az eredményre jutottak, hogy a Hold évente átlagosan 3,8 cm-rel jut messzebb. A Földön pedig egy nap időtartama 100 évenként 2,5 ms-mal nő. Hasonló eredményt mutat a régi korok észleléseinek összegzése, főleg a fogyatkozások időpontjainak lassú csúszása révén. Ezen a téren elsősorban az igen pontos kínai adatokra támaszkodtak.

Árapálytérképek segítségével, amelyeket kiszámítanak az egyes földtörténeti korokra. Ezen a téren legfeljebb 560 millió évre visszamenőleg lehet megbízható adatokhoz jutni. Azt még így is tudjuk, hogy a Föld forgásátelsősorban az óceáni árapály fékezte.

Több forrás szerint, mintegy 300-150 millió évvel ezelőtt a fékező forgatónyomatéknak minimuma volt. Ez a Pangea szuperkontinens kialakulásával magyarázható, mivel ezáltal a súrlódást növelő selfek területe erősen összezsugorodott.

Az innen kapott adatokat extrapolálták nagyobb időtartamokra, és azt kapták, hogy 4-4,5 milliárd éve a Hold 320-315 ezer km-re volt a Földtől, azaz 15-18%-kal volt közelebb. Ez azért is hihetőnek tűnik, mert az óceánok csak kb. 3,5-4 milliárd éve alakulhattak ki, s a távolodás is ekkor gyorsulhatott fel. Másrészt, arra is utal, hogy a Hold-Föld rendszer viszonylag rövid idő alatt képződhetett még a Föld ifjúkora idején, amivel alátámasztani látszik az óriás ütközés elméletet (Varga,1994).

Meddig távolodik a Hold? A Föld forgási periódusa folyamatosan nő; ezzel együtt, de nála lassabban a Hold keringési periódusa is. Ha a Föld forgásánál gyorsabban keringene, akkor a dagályokat előresiettetné, s azok gyorsítanák a bolygó forgását, miközben a Hold fékeződve közelebb kerülne, egyre gyorsabb pályára lépve. A kettős rendszer mindkét esetben ugyanahhoz a végállapothoz konvergál: a szuperkötött állapothoz, amelyben a Föld és a Hold összes rotációs és egymás körüli keringési periódusidői megegyeznek egymással. Ekkor a két égitest egymásra gyakorolt árapályhatása 0 lesz. A Napé azonban még nem, hiszen az a Föld forgását akarja hasonlóan kötötté tenni, vagyis hogy egy évig, 365 mai napig tartson egy nap a Földön. Ezért a Föld forgási periódusideje tovább nő, s a Hold azt követni szeretné, maga is tovább fékeződve.

 A Hold kötött forgása

Itt csak a szilárd tengerjárások léteznek, de ezek hasonló hatásúak, mint a Föld óceánjaiban. Vegyünk először egy homogén sűrűségű, teljesen gömbszimmetrikus holdat, amely körpályán kering egy másik, nála nagyobb tömegű égitest körül, és a forgástengelye merőleges a keringési síkra. Erre az árapályerő - a teljes szimmetria erőkiegyenlítő hatása miatt - nem képes forgatónyomatékot kifejteni. Ám az alakját - a szimmetria megbontásával - maga az árapály torzítja el, ugyanúgy kb. ellepszoid alakúvá deformálva, mint a földi tengerjárásoknál. Igaz, a szilárd dagályok nagyon kis szintkülönbséggel járnak, de ez már elég, hogy az árapály forgatónyomatékot fejtsen ki rá. Ha a hold tengely körüli forgási szögsebessége nagyobb, mint a keringéséé, ugyanúgy magával ragadja a két dagálypúpot, mint a Földön a súrlódás a tengeri dagályokat. A különbség itt csak annyi, hogy a súrlódás helyett a hasonlóan működő deformáció-tehetetlenség késlelteti a dagály beállását a két égitest tömegközéppontjait összekötő egyenesre. Az eredmény is hasonló: a hold forgása lassul, a (közös tömegközéppont körül keringő) anyabolygó pedig távolodik tőle. Ha a hold forgása lassabb, akkor a dagálypúpok lemaradnak, s az árapály siettetni próbálván őket, felpörgeti a holdat, miközben az anyabolygó perdületet veszít, s közeledik hozzá. Mindkét folyamat a kötött állapot beálltával ér véget, amelyben tehát a hold tengelyforgási és keringési szögsebessége megegyezik. A gondolatmenet általánosítható ellipszispályára, tetszőleges formájú holdra vagy a pályára nem merőleges, de még 0-tól különböző hajlásszögű forgástengelyre, így a mi holdunkra is (Horváth,1991). A Föld már nagyon hosszú ideje kötötté tehette, és ezt azóta is fenntartja. Ha ui. a Hold távolodik tőlünk, akkor a keringési ideje is folyton nő. Ezért a Föld a Hold forgását állandóan utánaállította, s a két periódusidő ma is megegyezik.

 A HOLD HATÁSAI A FÖLDI ÉLŐVILÁGRA

 A HOLD KELETKEZÉSÉNEK HATÁSA

Hogy erről valamit mondjunk, biztosan tudnunk kellene, hogyan is jött létre a Hold. Feltételezzük, hogy a legvalószínűbb, az óriás ütközéses elmélet a helyes. Milyen következményei lehettek egy ilyen, legalább marsméretű égitest becsapódásának?

 A KÖZVETLEN KÖVETKEZMÉNYEK

A földpálya változása. Ennek természetesen komoly következményei lehettek az éghajlatra, de az egész Föld, sőt, a többi bolygó sorsára is. Mivel újabban a planetezima sebességét 11 km/s -re becsülik (2.1.3. fejezet), feltehető, hogy hátulról érte a Földet (erről lásd 4.3.1. fejezetet), vagyis gyorsította mozgását. Ezáltal a bolygó magasabb pályára kerülhetett, s így az általános földi klíma hűvösebb lett. Ha volt a sebességének jelentős, a Föld mozgására merőleges komponense, az a földpályát elliptikusabbá, nagyobb excentricitásúvá tehette. Ez a későbbiekben szélsőségesebb időjárás kialakulásával járhatott. Mai tudásunk azonban még nagyon bizonytalan, tehát minden következtetés erősen esetleges, a Föld pedig sem elnyúltabb, sem „körösebb" pályán nem mozog, mint „kellene".

A forgás. Az ütközés biztosan erősen megbillentette a forgástengelyt, bár nem tudni arról, hogy ennek utólag nyoma lenne. A Föld szögsebessége is módosult, az utóbbi időben pl. felteszik, hogy egy Marsnál kb. kétszer nagyobb tömegű bolygó érkezett, amely ( 2.1.3. fejezet) a Föld forgásával ellentétes irányban csapódhatott be; tehát fékezte azt. Eszerint bolygónk korábban akár sokkal gyorsabban is foroghatott.

Geológiai behatás. Abban az időben a Földnek már egy - viszonylag vékony - szilárd kérge lehetett, amelyet a belerohanó planetezima bizonyosan átütött. Az ezt követő nagy erejű robbanás lehámozta a kéreg és a köpeny nagy részét - számítógépes szimulációk arra utalnak, hogy a Föld gömb alakja is eltorzult. Az olvadt, forró kőzetek azután azt lassan helyreállították, s később a felszín is újraképződött. Bizonyos teóriák szerint az ütközés nagy érintőirányú lökést adott a Földnek, amely elindíthatta a gyors köpenyáramlást. Ennek a lemeztektonikai folyamatokban lett komoly szerepe később. A magban is nyoma maradhatott a kataklizmának: külső részében ez indíthatta el azt az örvénylést, amelyek a Föld szokatlanul erős mágneses terét okozhatja, de a belső rész alakját és rezgését is módosíthatta (Illés, 1995).

Végső soron, a becsapódás megváltoztathatta akár a Föld egész geológiai történetét, pl. a leendő kontinensek, a kéreglemezek elrendeződését (Comins, 1994).

 A LÉGKÖR ÁTALAKÍTÁSA

A Föld eredeti, ún. primer légköre a Nap és a gázbolygók kialakulásához fel nem használódott, „visszamaradt" gázokból, főként hidrogénből és héliumból állhatott, amelyek átmenetileg bolygónkhoz csatlakozhattak. Ez egy igen ritka gázkeverék volt, amit azonban a Holdhoz hasonlóan, a Föld sem tudott megtartani. A napszél és a szintén a Napból érkező hő ezt a „levegőt" gyorsan eltávolította a felszínről (Comins, 1994).

A szekunder légkör. A nehéz szén-dioxid-, nitrogén-, és vízmolekulákat már itt tudta tartani a Föld. Ezek gáz halmazállapotban igen nagy mennyiségben találhatóak a mélyben, a kőzetekben abszorbeálódva; a felszínre a tűzhányók kitörései során, és egyes mély repedéseken át érkeznek. Néhány 100 millió év alatt lassanként felgyülemlettek, s ők alkották a Föld új atmoszféráját, amely kb. 96%-ban CO₂-ből állt, a többi túlnyomórészt a ma is meglévő N₂, és H₂ készletek voltak. A szekunder légkör tehát vulkáni eredetű volt, s a mostaninál kb. 100-szor sűrűbb lehetett. Megjegyezhetjük, hogy hasonló a helyzet a többi Föld-típusú kőzetbolygónál is (amelyiknek van, mert pl. a Merkúrnak gyakorlatilag nincs légköre). Az akkori földi viszonyok leginkább a mai Vénuszra emlékeztettek. A nagy nyomású, sűrű, CO₂-ben gazdag, üvegházhatást keltő - azaz forró - légkör nem ígért túl nagy jövőt az esetleg kialakuló élőlényeknek.

Ha a Holdat „kirobbantó" óriás ütközés el is marad, a Föld fejlődése mindenképp más irányt vett volna, mint pl. a Vénuszé. Mivel messzebb van a Naptól, a Földön a hőmérséklet egy idő után eléggé lehűlt volna ahhoz, hogy a víz kicsapódjon a levegőből, s kialakulhatnak az óceánok, amelyek a CO₂ nagy részét elnyelnék. A földi élet is valószínűleg létrejött volna. (Ennek meggyorsításában - a valóságban - a Hold is részt vett, lásd a 4.2.1.1. fejezetet.)

Maga az ütközés az élőlények későbbi sorsát befolyásolhatta. A hatalmas robbanás ugyanis a légköri gázok nagy részét kisöpörte az űrbe; többségük ezután már nem is jött vissza. A kirobbantott kőzet is sok CO₂-t tartalmazott, amelynek nagy része később a légkörbe kerülhetett volna. Ez azonban most az elpárolgott anyagokkal együtt szintén kisodródott a világűrbe Az eredeti atmoszféra mintegy 15%-a a bolygó számára elveszett.

Tudjuk, hogy a mai földi levegő oxigéntartalma kizárólag az autotrof élőlényeknek (ilyenek pl. a zöld növények, vagy a baktériumok egy része) köszönhető, amelyek a fotoszintézis során a CO₂-t lebontják, és szerves anyagokat építenek fel belőle. A gázmolekula szétbontása során oxigén is keletkezik, amelynek egy részét nem tudják felhasználni a cukrokhoz és egyéb összetett szerves anyagokhoz, ezért egyszerűen kilélegzik. Ez az elem igen reakcióképes, ezért először a felszínen található éghető anyagokkal, főleg a vassal egyesülne, s csak ezt követően, kb. 750 millió évvel a Föld keletkezése után kezdett nagy mennyiségben felhalmozódni. Ám, ha az ütközés elmarad, az élőlényeknek a valóshoz képest jelentős, +15%-os szén-dioxid-többlettel kellett volna megbírkózniuk, ezért az egész jóval tovább tarthatott volna, talán 1 milliárd évig is. Az oxigénlégkör teljes kialakulása pedig ezután még félmilliárd évvel tovább tartana. Mindez a heterotrof élőlények kialakulását és további fejlődését is hátráltatta volna (ilyenek az állatok és a gombák, amelyek végső soron mind a növények által előállított szerves anyagokat fogyasztják), a későbbiekben viszont a túl nagy oxigénkoncentráció veszélyeztetné őket. Az élőlények ehhez még éppen tudnának alkalmazkodni anélkül, hogy elégnének. A levegő maga is sűrűbb lenne; nagyobb CO₂-tartalma erősebb üvegházhatást idézne elő, miáltal az éghajlat melegebb és a - sok elpárolgott víz révén - nedvesebb is lenne.

Az ütközés hiányában tehát a földi evolúció jelentős, sok száz millió éves késedelmet szenvedhetett volna, ugyanakkor az eltérő légnyomás, gázösszetétel és klíma az evolúciót is egészen más irányba terelné.