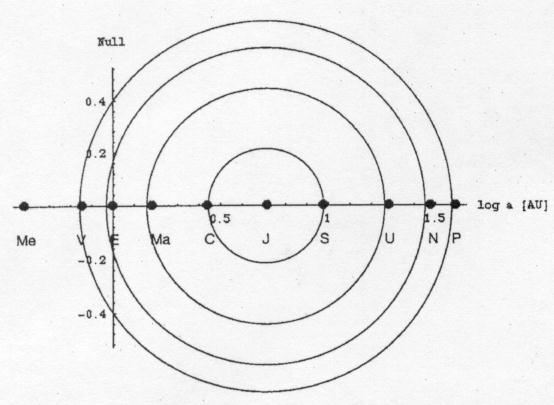
13. ábra: A bolygópályák
Jupiter-központú logaritmikus szimmetriája
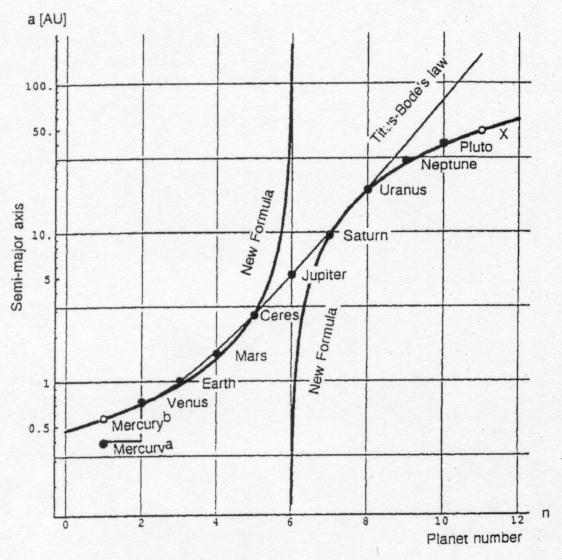
14. ábra: A Ragnarsson-formula
a határokon is jobban illeszkedik, mint elôdje
Sokáig úgy hittük,hogy a bolygótávolságok szabályszerûségérôl az empírikus úton talált Titius-Bode formulánál nem sikerül jobb összefüggést megadni, amely akár pontosabb lenne nála, vagy esetleg meg is tudná magyarázni, hogy a bolygók miért azon szabályszerûség szerint helyezkednek el, amit mi a pályáikból kiolvasunk.
Aztán 1994-ben Sven-Ingmar Ragnarsson, aki a Svéd Ipari és Technikai Fejlesztési Társaság tagja (Swedish Board for Industrial and Technical Development), új modellel lépett színre. Egy új, bár szintén empirikus formula segítségével próbálta a Naprendszer bolygóinak relatív távolságát egyszerûen megadni. Ráadásul azontúl, hogy a képlet matematikailag ugyanolyan egyszerû, mint a Titius-Bode féle összefüggés, még pontosabb is. Ezenkívül elôdjénél valósabb fizikai tartalmat is hordoz, mint például a bolygók Jupiter körüli szimmetriája, vagy a gravitációs rezonancia. Sôt, ami számunkra igazán fontos, hogy ez a Jupiter-központú szimmetria felveti az esetleges X. bolygó létét is.
3.1 A TITIUS-BODE SZABÁLY KRITIKUS SZEMMEL
A több mint 200 éves Titius-Bode szabály egy szimpla matematikai kifejezés, amellyel úgy tûnt meg lehet becsülni a Naprendszer jelentôsebb égitestjeinek távolságát, kivéve a legkülsô, akkor még felfedezetlen bolygókét (némelyikük felfedezésében volt is némi szerepe magának a Titius-Bode szabálynak is).
Az összefüggést leggyakrabban az alábbi módon szokták interpretálni:
a=0.4+0.3×2n-2,
ahol "a" a Nap körül keringô égitest pályájának fél nagytengelye csillagászati egységekben (AU) kifejezve, "n" pedig a bolygó sorszáma a Naptól távolodó sorrendben. Ahhoz, hogy az elsô bolygó, a Merkúr távolságára is elfogadható értéket kapjunk, rögtön egy kis csúsztatással kell élnünk, azaz "n" helyére kénytelenek vagyunk 1 helyett mínusz végtelent helyettesíteni.
A Titius-Bode szabályt gyakran említik csillagászati témájú könyvekben, mint a bolygótávolságokban felismerhetô törvényszerûséget, különös tekintettel az aszteroida-övezetre, amely elhelyezkedése ezáltal magyarázatot nyer. Bár ezt a szabályt gyakran alkalmazzák a különbözô naprendszer-keletkezési elméletek próbájaként is, úgy tûnik, semmilyen releváns fizikai tulajdonságot sem rejt maga a kifejezés. Számos kísérlet történt már az évek során a módosítására, pontosítására (Nieto, 1972). Néhány ezek közül többé-kevésbé komplex módon, különbözô algebrai és trigonometrikus korrekciókkal kísérletezett a mozgások és erôtörvények értelmezésénél, hogy ezek segítségével hozzávetôleg helyes értékeket adjon meg a bolygótávolságokra (Blagg, 1913; Richardson, 1945; Neuhä user,Feitzinger, 1986), de igazából nagyon kevés számítás vette figyelembe a Naprendszer valódi fizikai adottságait.
Matematikai bolygókeletkezési modelleknél más-más szabályszerûséget fedeztek fel (Dole, 1970; Hills, 1970; Torbett, 1982). Közös ezekben a formulákban, hogy a bolygók elhelyezkedése valamilyen törvényszerûséget követ. Ez azt jelenti, hogy van némi kapcsolat a szomszédos bolygók távolsága között, amibôl következik, hogy bizonyos bolygópályákat a protoplanetáris ködben lejátszódó folyamatok általánosan determináltak. Graner és Dubrulle egy korábbi, 1994-es tanulmányában kifejtette, hogyan vezethet a rotációs és skálainvariancia Titius-Bode-szerû összefüggésekre ezen folyamatok lejátszódása során.

13. ábra: A bolygópályák
Jupiter-központú logaritmikus szimmetriája

14. ábra: A Ragnarsson-formula
a határokon is jobban illeszkedik, mint elôdje
3.2 NAPRENDSZERÛNK SZIMMETRIÁJA
Ha ábrázoljuk a bolygók Nap körüli pályáinak a fél nagytengelyeit (a) logaritmikus skálán (13. ábra), a Jupiterhez viszonyítva szimmetriát figyelhetünk meg. Ezzel a szimmetriával még nem nagyon foglalkozott Ragnarsson (1994) elôtt a szakirodalom.
A Titius-Bode szabály az elsô nyolc bolygó esetén elég szép eredményt szolgáltat a Naptól mért távolságokra, beleértve a kisbolygóövezetet is (s figyelembe véve a Merkúr sorszámánál elkövetett csalást), de a Neptunusz és a Plútó távolságának meghatározására már nem alkalmas.
Azonban ha a Jupitert helyezzük a középpontba, s körötte figyeljük a bolygók elhelyezkedésének szimmetriáját, akkor magától értetôdôen látszik az ábra alapján is, hogy a Neptunusz és a Plútó távolsága logaritmikusan egybevág a Föld, illetve a Vénusz távolságával a Jupitertôl ellentétes irányba haladva. Sôt, az ábra alapján az is látszik, hogy minden bolygónak megvan a maga párja ebben a Jupiter-középpontú logaritmikus szimmetriában: a Jupiterhez legközelebb esô nagybolygónak, a Szaturnusznak a belsô bolygók közül a Ceresszel fémjelzett aszteroida-övezet lesz a párja, az Uránusz Jupitertôl való logaritmikus távolsága a Marséval egyezik meg, a Neptunusz párja a Föld, a Plútóé a Vénusz. A legbelsô Merkúrnak azonban nincs külsô párja. Amennyiben sikerülne bebizonyítanunk, hogy Naprendszerünk legnagyobb tömegû bolygója gravitációjával tényleg befolyással van a többi bolygó elhelyezkedésének alakulására, azaz ha ezen szimmetria mögött sikerülne esetleg a bolygók kialakulásával is kapcsolatos fizikai tartalmat megsejtenünk, akkor lehetne némi alapunk arra, hogy elkezdjünk Naprendszerünkben egy tizedik nagybolygó után is kutakodni. Ezáltal válhatna tökéletessé ez a szimmetria-elmélet. Esetleg a Merkúr Jupiterhez képesti elhelyezkedésébôl a szimmetria alapján megpróbálhatnánk megbecsülni a keresett égitest, vagy égitestcsoport (hiszen például az aszteroida-övezet helyén is bolygót sejtettek hajdanán) Naptól, illetve a Jupitertôl való távolságát is.
A felfedezett szimmetriából adódóan logikusan hangzik a bolygótávolságok Jupiter-centrikus felvétele. A csillagászati egység analógiájára bevezethetô a "jupitertávolság" egység, azaz a Jupiter Naptól mért távolsága, mint alapegység (1 egység=5.203 AU; 5. táblázat). Elsô közelítésben úgy tûnik, hogy a bolygótávolságok a Jupiter-Nap távolság 1.8-szeresei, vagy ennek többszörösei, belsô bolygók esetén hányadosai. Pontosabb kiértékelésnél 1.84-nek adódik ez a szorzótényezô. Ha még pontosabban szeretnénk ezt a számot felírni, esetleg tört alakban, akkor azt vehetjük észre, hogy 1.842 nem más, mint (5/2)2/3. Ha egy bolygó Nap körüli pályájának fél nagytengelye a Jupiter-pálya fél nagytengelyének (5/2)2/3-szorosa, akkor e távolsághoz a Jupiter Nap körüli keringési periódusának 5/2-e tartozik, ahogyan az Kepler III. törvényébôl számolható. Ez az 5/2-es érték egyébként egyike a legjellemzôbb, legstabilabb gravitációs rezonanciáknak. Hills kompjúter-szimulációs modelljei (1970) megerôsítik, hogy az 5/2-es arány a leggyakoribb a stabil pályák periódus-arányainál.
A fentieket figyelembe véve, a következô módon adhatunk meg egy formulát, amely az összes ismert bolygó távolságát jó közelítésben megadja, AU-ben kifejezve:
a' =aJ [ (5/2)2/3| m| ] sign(m),
ahol "a'" az "n"-dik bolygó (kezdve a Merkúrral, ahol n=1) pályájának a fél nagytengelye, "aJ" a Jupiterpálya fél nagytengelye, ami 5.203 AU. Az m=n-6 paraméter a bolygó Jupiter-centrikus sorszáma, így "m" a belsô bolygók esetén negatív, | m| az "m" abszolútértéke, és sign(m)= 1 ha m>0, -1 ha m<0, 0 ha m=0.
A konstansok behelyettesítésével és kiszámításával az elôbbi egyenlôség tovább egyszerûsíthetô:
a'=2.825/m AU a belsô bolygókra,
=5.203 AU a Jupiterre,
=9.584×m AU a külsô
bolygókra.
Az új formula abban különbözik a Titius-Bode szabálytól, hogy a bolygókat három csoportra bontja. Maga a Jupiter egy különálló pont, míg a külsô bolygók távolságát egy egyszerû lineáris függvény írja le, azaz a bolygópálya fél nagytengelyének a nagyságát úgy kapjuk, hogy a Jupiter-pálya fél nagytengelyét megszorozzuk annyiszor 1.842-vel, ahányadik bolygó távolságára kíváncsiak vagyunk a Jupitertôl kezdve. Például ha a keresett X. bolygó Naptól mért távolságára vagyunk kíváncsiak:
5×1.842×5.203 AU=47.92 AU,
mivel a tizedik bolygó a Jupitertôl számítva az ötödik, a Jupiter-pálya fél nagytengelye pedig 5.203 AU.
A belsô bolygókra nézve a függvény egy fordított arányosság, azaz a bolygópálya fél nagytengelye egyenlô a Jupiter-pálya fél nagytengelye osztva annyiszor 1.842-vel, ahányadik a bolygó a Jupiterhez képest. Például a Föld esetén, amely a Jupiterhez képest a harmadik belsô bolygó (nem feledve az aszteroida-övezetet):
5.203/(3×1.842)=0.942.
(A Ragnarsson-formulából kapott pályaadatok az 5. táblázatban olvashatók.)
A Titius-Bode szabály jó közelítést ad mind a külsô, mind a belsô bolygók esetén, a szélsôértékektôl eltekintve (Merkúr, illetve Neptunusz, Plútó). A Jupiter-központú szimmetria, s az ebbôl származtatott Ragnarsson-formula még evidensebbé válik, ha a koordinátarendszerben a bolygók sorszámához rendeljük hozzá a pálya fél nagytengelyének logaritmusát (14. ábra). Látható, hogy ez a függvény együtt görbül a széleken is a valós értékekkel, amire a Titius-Bode-féle lineáris szabály nem volt képes. Azt mondhatjuk, hogy az új formula a határokon is képes megállni a helyét, ami indokolttá teheti a mögötte álló tartalom (Jupiter-központú, gravitációs rezonancián alapuló szimmetria, X. bolygó feltételezése) valószerûségének megfontolását, megvizsgálását, illetve a formula Titius-Bode szabállyal szembeni preferálását.
A Titius-Bode szabályból
számolt adatok:
| Bolygó neve | Bolygó sorszáma |
(avalódi) |
(aTitius-Bode) |
centrikus hiba |
centrikus hiba |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Relatív hiba átlaga Merkúr a esetén; heliocentrikus:13.55%, Jupiter-centrikus:19.05%
Merkúr b esetén; 17.43% 18.97%
A Ragnarsson-formulából
számolt adatok:
|
|
|
|
egységekben (5.203 AU) |
(avalódi) (AU) |
(aRagnarsson) (AU) |
(%) |
(%) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Relatív hiba átlaga Merkúr a esetén; heliocentrikus:1.86%, Jupiter-centrikus:0.84%
Merkúr b esetén; 2.58% 0.64%
Megjegyzés: a Titius-Bode formula felírásánál eltértem a megszokottól, s "n" helyett "n-2"-t szerepeltettem, érthetôségébôl így sem vesztett, viszont jobban szinkronba hozható volt a Ragnarsson formulával.
3.3 SZIMMETRIÁBÓL KOZMOGÓNIÁBA
Az elôzô fejezetben megismert szimmetria és szabályszerûség közelebb vihet minket a Naprendszer kialakulásával kapcsolatos megállapításokhoz, s méginkább ahhoz, hogy a bolygók milyen módon képzôdhettek.
Általánosan elfogadott nézet, hogy a Jupiter volt az elsô, amelynek anyaga összeállt bolygóvá, lejátszódott a kondenzáció és az akkréció, s ezután az összes többi bolygó képzôdése teljesen az ô befolyása alatt játszódott le a Naprendszerben. Ezen elmélet kedvelt forgatókönyve, hogy az örvénylô protoplanetáris korong könnyebb gáz- és porrészecskéi, a Nap fúziójának beindulása után a napszél által kifújódtak a Naprendszer külsôbb régióiba, egészen addig, amíg bizonyos távolságra az egyre inkább összenyomódott gáz- és porfelhô ezt a folyamatot le nem állította (ez a folyamat egyébként azt is világossá teszi, hogy az óriásbolygók miért gázóriások). Az ennek eredményeként képzôdött gyûrûben a relatív nagyobb sûrûségnek köszönhetôen jóval gyorsabban összeállt az anyag egy, vagy több bolygókezdeménnyé, amely aztán egy óriási planétává, a Jupiterré egyesült. A Szaturnusz távolságában is elegendôen nagy anyagsûrûség volt egy viszonylag gyors kondenzációhoz és akkrécióhoz, amit még a Jupiter gravitációs rezonanciája fel is gyorsított. A gravitációs rezonanciák miatt egyre szûkebb helyre kényszerültek a por- és gázanyagok, planetezimálok, amelyeket a Kirkwood-zónák osztottak csoportokra. Ellenkezô esetben egy második óriásbolygó jött volna létre.
Az 5. táblázat adatainak mélyebb vizsgálata alapján arra juthatunk, hogy az új formula segítségével kapott távolságoktól való kisebb eltérés egy másodlagos Szaturnusz-szimmetriát mutathat. Miután a Szaturnusz a Jupiterhez képesti majdnem 5/2-es arányú pályáját feltérképezték, jött a gondolat, hogy a Jupiter és a Szaturnusz együttes hatása felelôs a többi planéta pályáinak elkülönítéséért. Ha igaz a Jupitert és esetleg a Szaturnuszt is figyelembe vevô szimmetria, akkor ez azt jelenti, hogy a külsô bolygók elhelyezkedését elsôsorban a Jupiter, másodsorban legközelebbi külsô szomszédja határozza meg.
A folyamat alpján szintén nyilvánvaló, hogy a ködkorong belsô részébôl eltûntek a könnyebb elemek, amely egy kisebb, nehezebb elemekben gazdag belsô korongot eredményezett, amelybôl a Föld típusú bolygók alakulhattak ki. A pályákat aztán nagyjából hasonló mechanizmusok szabták meg, mint a külsô bolygókét.
Torbett és munkatársai nagy, Jupiter-méretû égitest hatásait vizsgálták (1982) bolygórendszerek képzôdésekor, melynek során 2:1 rezonanciával dolgoztak a belsô, és 1:2 rezonanciával a külsô bolygók esetén. Modelljük, bár jól illett például a Vénuszhoz, többek között a Neptunusz kialakulására, pályájára nem adott jó közelítést, szemben a Ragnarsson által alkalmazott 5/2-es szimmetriával, amely a tapasztalatok szerint stabil pályák esetén gyakoribb is.
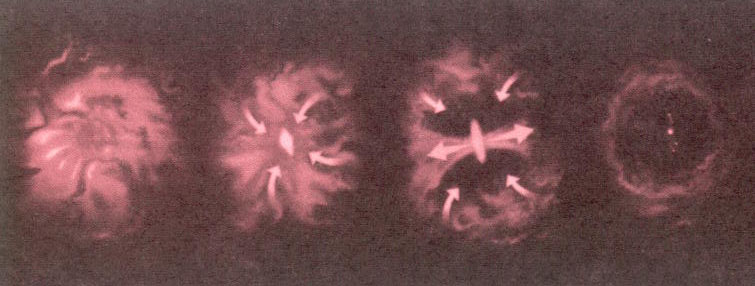
15. ábra: Mai naprendszer-keletkezési
elképzelés
3.4 AZ ÚJ FORMULA PONTOSSÁGÁRÓL
A Ragnarsson-formula alapján számított bolygótávolságok relatív hibáját két módon vizsgálhatjuk: egyrészt hagyományos szemléletünket követve, azaz a relatív hibát a Naptól mért távolság eltéréseibôl számoljuk; vagy a többiek keringésére legnagyobb hatással lévô központtól, a Jupitertôl való távolsághoz képesti eltérést adjuk meg (5. táblázat).
Elôször hasonlítsuk össze a Naptól mért távolságokban keletkezô hibákat. Azt már korábban is említettük, hogy a Titius-Bode szabály esetén elég nagy hibaszázalékkal találkozhatunk, fôként a külsô bolygók, s a Merkúr valós sorszáma esetén. Az összes bolygóra kivetített hibaszázalék 17.43%, a Ragnarsson-formula estén összességében pedig 2.58%-os hibáról beszélhetünk, s az is látható, hogy egyes bolygók esetén is maximum kb. 7% a relatív hiba. Egyedül a Merkúrnál tûnik úgy, mintha még a Titius-Bode-nál is rosszabb eredményt kapnánk...
Azonban éppen ez a Merkúrnál tapasztalható rendellenesség lehet elméletünk helyességének egyik támasza. Milyen furcsa, a Ragnarsson-formula segítségével azt kapjuk, hogy a Merkúr Naptól mért közepes távolsága 0.565 AU (a valós 0.387), s a Titius-Bode szabály segítségével is 0.550 AU-t kapunk eredményül. Ez nem lehet véletlen, hiszen a Ragnarsson-formula esetében végig helyes eredményt kaptunk, ezzel az egy kivétellel. Azt mondtuk, hogy a Ragnarsson-formula segítségével úgy kaphatjuk meg egy belsô bolygó naptól mért távolságát, hogy a Jupiter-pálya fél nagytengelyét osztjuk annyiszor 1.842-vel, ahányadik a bolygó a Jupiterhez képest. Azonban, ha ugyanilyen módszerrel a Vénuszból, mint legbefolyásosabb égitestbôl indulunk ki, akkor azt kapjuk a Merkúrra, hogy:
a'=0.723 AU/1.842=0.393 AU,
s ez már igencsak megközelíti a valós 0.387-es értéket. Ez pedig azt jelentheti számunkra, hogy a Merkúrnál erôsebb a Vénusz gravitációs befolyása, mint a Jupiteré, hiszen sokkal közelebb van hozzá, s az eredmény is a Vénusszal való rezonanciára utal (persze a Nap közelségét sem szabad figyelmen kívül hagyni).
A fentiek is bizonyíthatják számunkra, hogy a gravitációs rezonancia igencsak befolyásolja a bolygók egymáshoz képesti elhelyezkedését a Naprendszerben, illetve más bolygórendszerek esetén is. Mivel a Naprendszerben a Jupiter a legnagyobb és legidôsebb bolygó, ezért ez az égitest az, amelyik már a Naprendszer keletkezésétôl befolyásolta többi társát, s ezért az ô gravitációs hatása figyelhetô meg legtöbb bolygópálya elhelyezkedésében. Mi sem bizonyítja ezt jobban, mint az, hogy a Ragnarsson-formula Jupiter-centrikus alkalmazása esetén az átlagos hibaszázalék 0.84%, s ez több, mint egy nagyságrenddel nagyobb pontosságot jelent, mint a Titius-Bode szabály számításai (5. táblázat).
3.5 RAGNARSSON A X. BOLYGÓRÓL
Amennyiben a továbbiakban úgy tekintünk erre az elméletre, mint egy lehetséges magyarázatra a stabil bolygópályákat illetôen, akkor ezen hipotézis alapján néhány merész következtetést is levonhatunk.
Már korábban is említettük, hogy ha a Jupitert vesszük centrumnak, akkor körülötte a többi bolygó logaritmikus szimmetriát mutat, amely alapján a Jupitertôl távolodva a bolygók párokat alkotnak: Szaturnusz-Ceres, Uránusz-Mars, Neptunusz-Föld, Plútó-Vénusz, a Merkúrnak pedig egyenlôre nincs párja a Naprendszerben, hacsak nem a feltételezett X. bolygó az. Ezáltal ez az egész harmonikus rendszer tökéletessé válna. A szimmetria alapján talált formula segítségével (a gravitációs rezonanciák alapján) meg is becsülhetjük a hipotetikus égitest távolságát. E szerint a X. bolygó kb. 48 AU távolságra kering a Naptól. Akkor eddig miért nem észleltük?
Lehet, hogy pályája legtávolabbi pontján jár, ami lehet, hogy még a Plútó pályájánál is elnyúltabb (hiszen Napközelben a Neptunusz közelében kell elhaladnia, hogy perturbálhassa annak pályáját), s az is elôfordulhat, hogy a megadott távolságban csak aszteroida méretû égitesteket találunk, ami a Kuiper-övben nem is meglepô...