Idáig áttekintettük, hogy milyen fontos szerepe is van a csillagászatban a változócsillagok kutatásának, ezen belül pedig a periódus pontos meghatározásának. Nem véletlen, hogy a különböző módszereknek nagy irodalma is van. A továbbiakban röviden áttekintjük a Fourier-transzformáció alapjait, mert ez az egyik legelterjedtebb módszer, valamint sok más eljárás alapja, majd rátérünk az idő-frekvencia eloszlások ismertetésére.

Legyen az analizálandó jel s(t), ennek Fourier-transzformáltja (Hesselmann: Digitális jelfeldolgozás):

 . (3.1)

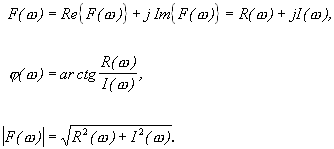
Értelmezett az inverz transzformáció is:

 . (3.2)

A gyakorlatban, csillagászati alkalmazásoknál azonban nem folytonos jelekkel van dolgunk, hanem mintavételezett jelekkel, sőt gyakran nem egyenletesen mintavételezett jelekkel. Ezért szükséges bevezetni a Fourier-transzfomáció diszkrét változatát, nyilván az integrál helyett diszkrét összeget kapunk:

 . (3.3)

Itt  utal a diszkrét időpontokra, ahol a jel mintavételezve van. Amennyiben a mintavételezés nem egyenközűen történt,  -al helyettesítendő, ahol  az adatsor kezdőpontjához tartozó idő. Bár nem említettük, de érvényes a Shannon-féle mintavételezési törvény, azaz a mintavételi frekvenciának a jelben előforduló legnagyobb frekvencia kétszeresénél nagyobbnak kell lennie ahhoz, hogy a jel információtartalmát teljesen visszakaphassuk. Ekkor a mintavétel időközére a következő összefüggést kapjuk:

.

Az adatsor általában azonban nem a teljes (végtelen) időskálán áll rendelkezésre, hanem egy  időablakon belül, ezért a (3.3)-ban még folytonos spektrum is diszkrét értékekben lesz csak adott (N adat esetén):

 , (3.4)

Bizonyítás nélkül megjegyezzük még, hogy a (3.4)-el adott  nem egyezik meg (3.3)-ban adott -val, hanem attól egy úgynevezett ablakfüggvénytől függő skálatényezőben különbözik. A véges időtartamon adott jelet ugyanis matematikailag úgy értelmezhetjük, hogy a végtelen jelet megszorozzuk egy ún. ablakfüggvénnyel. Ez a frekvencia térben a (végtelennek tekintett) jel Fourier-transzformáltjának az ablakfüggvény transzformáltjával vett konvolúciójának felel meg. Legegyszerűbb esetben az ablakfüggvény egy derékszögű ablak, azaz értéke 1 a megfigyelés időtartama alatt, azon kívül pedig nulla. Ebben az esetben ez a bizonyos skálázó tényező  lesz (választhatók másmilyen ablakok is, ekkor a spektrumnak más és más tulajdonságai lesznek, ezt azonban nem célunk most vizsgálni). Derékszögű ablak esetén tehát a konkrét számításra is alkalmas forma:

 . (3.5)

 

A hagyományos Fourier-analízis tehát segít egy jel különálló frekvencia-komponensekre való bontásában, és meghatározza a komponensek relatív intenzitását. Azt azonban nem tudja megmutatni, hogy az egyes komponensek mikor is fordulnak elő a jelben. Előfordulhat az az eset ui. hogy az összetevők időben nem állandóak, a megfigyelés időtartama alatt a relatív intenzitások változhatnak. Vegyük példának egy hangszer hangját. Ha egy orgonán leütünk egy hangot, és kitartjuk azt pl. 3 percig, majd a jelet Fourier-analizáljuk, akkor megkaphatjuk a hang frekvenciáját (persze lesznek felharmonikusok is). Ha viszont az utolsó fél percben játszunk néhány ütemet Bach: d-moll toccata és fuga-jából, a Fourier-spektrum teljesen más lesz, sok különböző frekvencia fordul majd elő benne, de az nem derül ki, hogy a lényeges változás az utolsó fél percben történt. Természetes ötlet a spektrum időbeli változásának kiderítésére, hogy csökkentve az időablak hosszát, több spektrumot veszünk fel, és vizsgáljuk az egyes komponenseket, feltételezve, hogy azok az ablakon belül már állandóak. Sokszor nem áll ez fenn, valamint csökkentve az időablak szélességét, csökken a frekvencia-felbontás is. Természetesen nem csak (azt is mondhatnák hogy főként nem) a csillagászatban felmerült igények vezettek az idő- és frekvenciabeli változásokat együttesen leíró függvények tanulmányozásához. Egy olyan általános eloszlást kerestek, ami párhuzamosan adja egy jel intenzitását vagy energia-sűrűségét időben és frekvencia szerint. Ideális esetben egy ilyen eloszlást úgy kezelhetnénk és használhatnánk, mint bármilyen többváltozós sűrűségfüggvényt, azaz megkaphatnánk például a frekvencia-eloszlást egy adott időben kiintegrálva az időfüggést. Illusztrációként álljon itt egy egyszerű példa: az adatsor közepén a periódus a kétszeresére nő. Jól látható, hogy a Fourier spektrum is kimutatja mindkét periódust, azonban időben nem tudja elkülöníteni őket. Ezzel szemben a wavelet-térképről azonnal kiderül, hogy a két periódus elkülönül egymástól:

A Fourier-analízisből már ismert: egy s(t) jel pillanatnyi energiája:

intenzitás/időegység a t időpontban,

vagy

a  időtartamra jutó energia a időpontban.

Az intenzitás/frekvenciaegység, az energia-sűrűség spektrum a következőképp áll elő:

intenzitás/frekvenciaegység az  frekvenciánál,

vagy

a  frekvencia-tartományra jutó energia az  frekvenciánál,

ahol

.

A normálást úgy választottuk, hogy

a teljes energia = 1.

Az alapvető cél egy olyan időtől és frekvenciától függő függvény előállítása, amely energia vagy intenzitás/időegység/frekvenciaegység-et reprezentál. Legyen ez a közös eloszlás , ekkor:

intenzitás a időpontban és az  frekvenciánál,

a  idő-frekvencia cellára jutó energia a  pontban.

Ideális esetben felösszegezve az energia-eloszlást egy adott időpontban az összes frekvenciára, a pillanatnyi energiát kell kapjuk, és viszont, az összes időre összegezve egy adott frekvenciánál az energia-sűrűség spektrumot kapjuk (ezeket az összefüggéseket nevezzük marginálisoknak):

  (3.6)

,

ami a jel teljes energiájával lesz egyenlő, ha a marginálisok teljesülnek.

Több eloszlás-függvényt alkottak már, melyek teljesítik a marginálisokat, példaként megemlíthetjük a Wigner-Ville-, Kirkwood-, ill. Page-eloszlást:

                   (Wigner-Ville),

                                   (Kirkwood),

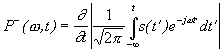                             (Page).

Az idő-frekvencia eloszlások általános elméletével Cohen (1989) foglalkozott részletesen, megadva egy általános függvény osztályt:

 , (3.7)

ahol  a kernel- vagy mag-függvény. Különböző mag-függvényeket választva különböző tulajdonságú eloszlásokat nyerünk.

A továbbiakban bemutatunk két különböző megközelítést idősorok idő-frekvencia analízisére. Az egyik az ablakozott (running window) Fourier-transzformáció általánosításából származó wavelet-transzformáció (esetünkben az ún. Morlet-kernellel), a másik pedig a Cohen-féle általánosított idő-frekvencia eloszlás a Choi-Williams magfüggvénnyel.

A bevezetőben már említett „klasszikus” eszköz idősorok analízisére a short-time Fourier-transzformáció, gyakran nevezik ablakozott Fourier-transzformációnak is. Az  jel egy időben lokalizált ablakfüggvénnyel () van súlyozva, majd Fourier-transzformálva (Kolláth, 1995):

.

Egy idősor wavelet-transzformáltja pedig a következőképp van definiálva:
 

 , (3.8)

ahol  a transzformáció kernel-függvénye,  ennek komplex konjugáltja, az b változó pedig periódus jellegű mennyiség. A fenti alakot a Parseval-formula alapján át lehet írni Fourier-transzformáltakra:

.

Válasszuk kernel-függvénynek a Morlet-kernelt (egy módosított Gauss-görbét):

,

ahol a és c skálázó faktorok ( általában). Ekkor a időeltolási paraméterhez és az f frekvenciához tartozó wavelet-transzformáció:

.

A gyakorlatban a DFT-hez hasonló módon bevezethető a Diszkrét Wavelet Transzformáció, mely szerint az amplitúdó spektrum (Szatmáry and Gál, 1992):

(3.9)

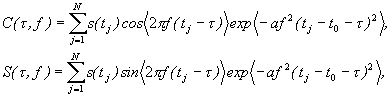
és  az adatsor első eleméhez tartozó idő.

A Gauss-ablak félszélessége a próbaperiódussal arányos, nem pedig állandó érték, mint a Fourier-analízisnél, így a frekvencia spektrumban a csúcsok félszélessége nem egyforma, hanem a frekvenciával arányosan növekszik. Az ablakot  értékkel toljuk el az adatsor elejétől a végéig, és minden eltolásra kiszámoljuk a frekvencia spektrumot.

Mint már említettük, a Cohen-féle általános idő-frekvencia eloszlás:

 . (3.10)

Amennyiben a mag-függvény helyére a Choi és Williams által javasolt exponenciális kernelt helyettesítjük, a Choi-Williams eloszlást kapjuk (CWD):

, ahol  a skálázó tényező.

A továbbiakban vizsgáljuk a CWD tulajdonságait. Tekintsük az  jelet több monoperiodikus komponens szuperpozíciójaként:

.

Az idő-frekvencia eloszlás az egyes összetevők eloszlásaiból (auto-terms) és a páronként különböző komponensek kölcsönhatásából (cross-terms) tevődik össze:

,

rövidített jelöléssel:

,

ahol

.

Ahogy látszik, a kereszttagok viselkedését a mag-függvény tulajdonságai határozzák meg. A kereszttagok többletet okoznak az eloszlásban, elfedhetik a valós energiaeloszlást bizonyos frekvencia- és időpontokban. A mag-függvény alkalmas megválasztásának épp az a célja, hogy a kereszttagok hatását minél inkább csökkentse. Azt azonban látni kell, hogy nem lehetséges olyan eloszlást előállítani, amelyik kielégíti a marginálisokat, viszont kereszttagok egyáltalán nincsenek benne. Helyettesítsük most be az exponenciális kernelt (3.10)-be:

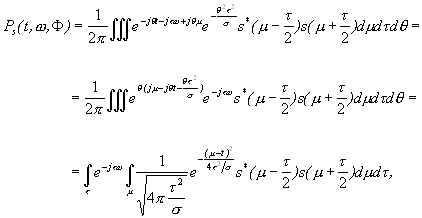  (3.11)

mivel

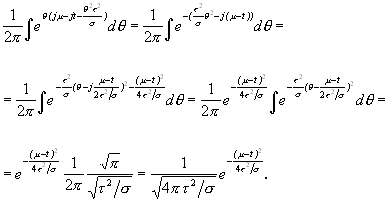
A Cohen függvény osztály tagjait értelmezhetjük egy  idő-indexelt autokorrelációs függvény Fourier-transzformáltjaként is:

,

ahol

 . (3.12)

A (3.12) egyenletből látszik, hogy -nek fontos szerepe van az autokorrelációs függvény tulajdonságainak meghatározásában. Egy időátlagolás túlzottan kisimítaná a jel gyorsan változó tulajdonságait, ezért a mag-függényt úgy kell megválasztani, hogy -nek nagy súlya legyen, amikor m közel van t-hez, illetve kis súlyt kapjon, mikor m távol van t-től. CWD esetén az autokorrelációs függvény a következő:

 ,  (3.13)

ami épp teljesíti a kívánt feltételeket, ha ugyanis  közel van -hez, akkor az exponenciális tényező miatt -nek nagy súlya lesz, ha  távol van -től, akkor épp ellenkezőleg. Az autokorreláció „mértékét” a  paraméter szabályozza, ha  nagy, akkor több szomszédos tagot használ , kisebb  esetén kevesebbet. , valamint  hatásának részletes vizsgálatát Choi és Williams végezte el. A  skálázó faktor szerepéről még annyit jegyzünk meg (bizonyítás nélkül, részleteket lsd. Choi and Williams, 1989), hogy egyfelől  nagy értékeire a Wigner-eloszlást kapjuk (), másrészt  mintegy szelektorként viselkedik a frekvencia felbontás és a kereszttagok csökkentése között. Ha -t nagyra választjuk, éles felbontást kapunk, több hamis csúcssal, míg kis -ra szélesebb csúcsokat kapunk, viszont kisebb a kereszttagok hatása. Gyorsan váltózó tulajdonságú komponenseket tartalmazó jelek analíziséhez tehát nagy -t kell választanunk (>1), lassabban változó jelekhez pedig kisebb -t érdemes választani (<1). Általában  értékét 0.1 és 10 között érdemes választani.

Csillagászati alkalmazásokban a vizsgált  jel korántsem folytonos, sőt gyakran nem is egyenletesen mintavételezett, így szükség van a CWD diszkrét formájának előállítására. Diszkrét idősorokra az általános idő-frekvencia eloszlás a következőképpen adott:

ahol  és  diszkrét változók,  pedig folytonos változók (ahol nem jelöltük, az összegzés -től -ig történik). Behelyettesítve a Choi-Williams féle mag-függvényt, kapjuk:

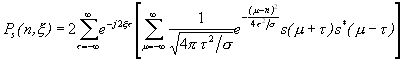 , (3.14)

mivel

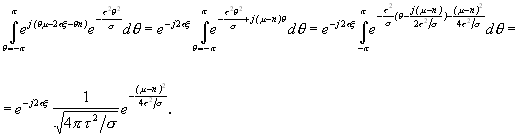
A levezetés során kihasználtuk, hogy  a  intervallumon kívül kicsi, ha .

Az s(t) jel természetesen nem a  intervallumon adott, ezért szükséges volt bevezetni a fenti transzformáció ablakozott változatát:

 

,

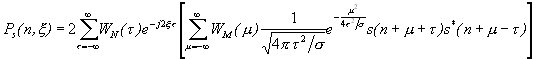ahol  egy szimmetrikus ablak, mely nemnulla a  értékekre,  pedig egy derékszögű ablak, melynek értéke 1 a  intervallumban. Tényleges számításokat a gyors Fourier-transzformáció segítségével érdemes végezni, e célból -t választva kapjuk:

 

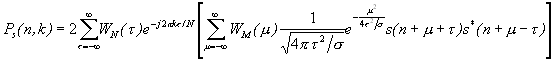(3.15)

ahol n az idő-index, k pedig a frekvencia-index. Az analitikus jelet két FFT-vel kaphatjuk meg, a valós jelre alkalmazva egy FFT-t, majd egy IFFT-t, majd kiszámolva az autokorrelációs függvényt a belső összegzésben, minden egyes időpontban egy újabb FFT-vel kaphatjuk meg az eloszlást. Nem egyenletesen mintavételezett jelek esetén az FFT-t DFT-vel helyettesíthetjük, bár ekkor a számítás lassabb lesz.