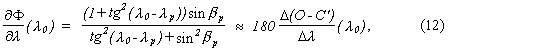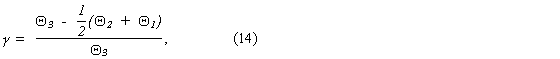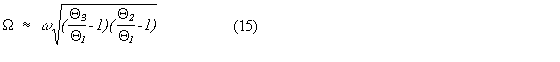ahol b/c és b/a a kisbolygó alakjának elnyúltságára
utalnak; az a,b,c kiterjedéseket a modellként alkalmazott
háromtengelyű ellipszoidok tengelyével szokták
definiálni, a>b>c értelemben
Ezen eljárás ("AM-módszer") hátránya,
hogy az amplitúdó alakfüggése csak hosszas megfigyeléssorozattal
küszöbölhető ki, de a pólus szélességére
még akkor sem várhatunk pontos adatot.
Michalowski (1993) összevonja a forgás és
az alak meghatározását úgy, hogy a különböző
fénygörbéket korreláltatja egymással.
Ez valóban nagy pontosságú periódusmeghatározást
tesz lehetővé, és jól megadja a pólus
koordinátáit is; ellenben valójában négy,
majdnem egyforma valószínűségű modellt
definiál, mert a forgásirány meghatározása
is bizonytalan, és  sem egyértelmű. Pontossága miatt azonban ez a módszer
ma már általánosan elfogadott.
sem egyértelmű. Pontossága miatt azonban ez a módszer
ma már általánosan elfogadott.
A kisbolygók modelljeit a bevezetésben már
említett módon adjuk meg. A sziderikus periódust napokban
szokás mérni, míg a forgástengely ekliptikai
koordinátáit fokokban. A háromtengelyű ellipszoid
modelljét az a/b, ill. b/c tengelyarányokkal jellemezhetjük.
A modell leírásához tartozik még a forgás
irányának megadása, azaz hogy a forgás a keringéssel
egyező, vagy ellenkező irányban történik-e.
Erre a P (prográd) és R (retrográd)
betűk utalnak .
4.3. Egy új módszer a forgásvektor meghatározására
Megvizsgálva az előző modellezési eljárások
által adott eredményeket, arra a megállapításra
kellett jutnunk, hogy a kapott eredmények ellentmondásait
nem megalapozott közelítések okozzák. Ezeket
a következőkben foglaljuk össze.
Egyrészt a szinodikus periódus meghatározásához
használt formulában szerepel két nem meghatározott
mennyiség, amelynek értékére mindössze
ésszerű becslések adnak közelítést.
Másrészt föltételezik, hogy a fényességmaximumhoz
tartozó aszteroida-felület, és így forgási
fázis, nem változik a keringés alatt. Ez az utóbbi
közelítés igaz ugyan a modellként használt
nem foltos ellipszoid esetében, de korántsem elhanyagolható
egy kisbolygó esetében. Ráadásul 1993 óta
a forgás fizikáját együtt állapítják
meg az alakkal, és így az alakmeghatározásban
rejlő hibák szintén kiütköznek a forgási
paraméterekben. Következésképpen valójában
4 lehetséges kisbolygómodell születik, amelyek egyrészt
a forgásirányban (P vagy R),másrészt a pólus
hosszúságában különböznek (egymáshoz
képest az eltérés kb. 180 fok).
Szem előtt tartva az eddigi módszerek hátrányait
és előnyeit, kidolgoztunk egy olyan egyszerű modellezési
eljárást, amely az eddigieknél pontosabban adja meg
a sziderikus periódust, valamint egyértelműen meghatározza
a forgásirányt. A pólus koordinátáinak
meghatározása is lehetséges, ennek pontossága
megegyező az előző módszerekével. Hibaanalízisünk
során meghatároztuk, hogy mekkora mértékben
eltorzuló fénygörbék analízise ad megbízható
eredményeket. Arra a következtetésre jutottunk, hogy
a kisbolygók nagy hányadánál alkalmazható
a módszer modellezésre. Sajnos önmagában ez az
eljárás sem ad egyértelmű értéket
a pólus szélességére, ehhez komplexebb vizsgálat
szükséges.
Az eljárás a kisbolygók fényességmaximumának
megfigyelésén és ennek földolgozásán
alapul. A
monoperiodikus, vagy ahhoz közeli viselkedésű változócsillagok
kutatásában széles körben használatosak
az O-C diagramok ('obszervált mínusz kalkulált', l.
pl. Szatmáry 1987), amelyek egy esemény megfigyelt és
számított időpontjának különbségét
prezentálják. (Ilyen esemény lehet például
egy pulzáló csillag maximumának bekövetkezése;
ennek kismértékű periódikus eltolódásaiból
pedig például kísérő komponensre lehet
következtetni.) Az O-C definíciója:

ahol tn az n-edik maximumidőpont
ideje, t0 egy kezdő maximumidőpont
('epocha'), P a periódus, n pedig a ciklusszám.
Ezt a formulát a következőképpen
értelmezhetjük kisbolygókra:
A kisbolygók forgási periódusa alatt
általában két maximumot figyelhetünk meg a fénygörbén,
amik a különböző oppozíciók alkalmával
más-más karakterisztikát öltve, gyakorlatilag
azonosíthatatlanok. Azonban pont a szimmetria miatt, azt mondhatjuk,
hogy a maximumok bekövetkezésének periódusa 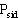 /2,
vagyis a sziderikus periódus fele, így ezzel a periódussal
vesszük föl az O-C értékeit. Azonban a kapott értékeket
nincs sok értelme időben ábrázolni, hiszen
a kisbolygó keringésére az idő nem jellemző
paraméter. A keringést vagy az aspect, vagy a geocentrikus
koordináták változásával prezentálhatjuk.
Esetünkben a geocentrikus koordináták figyelembe vétele
volt a kitűzött cél, így az O-C elméleti
értékeit is e koordináták függvényeként
állapítottuk meg. Ekkor újabb szimmetriák miatt
a 180-360 fokos ekliptikai hosszúságot vissza kell transzformálni
a 0-180 félkeringésbe, úgy, hogy az ekliptikai hosszúságoknak
csak a 180 fokos osztási maradékát vesszük figyelembe.
Alább taglalandó tézis szerint egy keringés
egy szinodikus fordulatot jelent, ami látszólag hozzáadódik
(prográd forgásnál kivonódik) a sziderikus
forgáshoz. Fél forgásra redukálva a periódust,
az O-C pontok 1 értékű változása már
fél forgás alatt bekövetkezik, ezért kétértelműségek
lépnének föl a teljes keringés vizsgálata
esetén. Ezért az
/2,
vagyis a sziderikus periódus fele, így ezzel a periódussal
vesszük föl az O-C értékeit. Azonban a kapott értékeket
nincs sok értelme időben ábrázolni, hiszen
a kisbolygó keringésére az idő nem jellemző
paraméter. A keringést vagy az aspect, vagy a geocentrikus
koordináták változásával prezentálhatjuk.
Esetünkben a geocentrikus koordináták figyelembe vétele
volt a kitűzött cél, így az O-C elméleti
értékeit is e koordináták függvényeként
állapítottuk meg. Ekkor újabb szimmetriák miatt
a 180-360 fokos ekliptikai hosszúságot vissza kell transzformálni
a 0-180 félkeringésbe, úgy, hogy az ekliptikai hosszúságoknak
csak a 180 fokos osztási maradékát vesszük figyelembe.
Alább taglalandó tézis szerint egy keringés
egy szinodikus fordulatot jelent, ami látszólag hozzáadódik
(prográd forgásnál kivonódik) a sziderikus
forgáshoz. Fél forgásra redukálva a periódust,
az O-C pontok 1 értékű változása már
fél forgás alatt bekövetkezik, ezért kétértelműségek
lépnének föl a teljes keringés vizsgálata
esetén. Ezért az
O-C(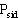 , l)
összefüggés helyett az O-C(
, l)
összefüggés helyett az O-C(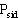 /2,
l mod 180) függvényt keressük.
Az előbb taglaltak alapján azonban e két kifejezés
formailag ekvivalens.
/2,
l mod 180) függvényt keressük.
Az előbb taglaltak alapján azonban e két kifejezés
formailag ekvivalens.
A fő stratégia ehhez a következő:
megforgatunk egy vektort (analógia: a kisbolygó) egy adott
tengely (analógia: forgástengely) körül, és
meghatározzuk, hogy különböző irányokra
(geocentrikus pozíció) mikor maximális a forgó
vektor vetülete (azaz mikor mutat fényességmaximumot
a kisbolygó). Ezt a helyzetet azzal a szöggel jellemezzük,
amit a forgó vektor az adott pozícióban egy fixált
referenciavektorral bezár. Ez a szög közvetlenül
megadja az
O-C értékét.
Tekintsük az alábbi két vektort:
b (cos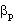 ,
0, sin
,
0, sin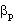 )
(4)
)
(4)
r (cosl, sinl, 0),
(5)
ahol b a forgástengely, r a megfigyelő
irányába mutató egységvektor, 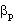 a pólus ekliptikai szélessége, míg l
az aktuális r és az (1,0,0) ('sub-ZPABP') vektor
közötti szög. Ez utóbbi, meglehetősen bonyolult
nevű vektor lényegében csak a koordinátarendszert
határozza meg azon feltétellel, hogy ezen rendszer X koordinátatengelye
irányából látunk minimális szög
alatt a forgásvektorra.
a pólus ekliptikai szélessége, míg l
az aktuális r és az (1,0,0) ('sub-ZPABP') vektor
közötti szög. Ez utóbbi, meglehetősen bonyolult
nevű vektor lényegében csak a koordinátarendszert
határozza meg azon feltétellel, hogy ezen rendszer X koordinátatengelye
irányából látunk minimális szög
alatt a forgásvektorra.
Vezessük még be a vn normálvektort
is, ami a kisbolygó fényességmaximumot adó
helyzetét jellemzi, amelynek a legnagyobb fényesség
állapotában merőlegesnek kell lenni b-re
és r-re egyaránt, azaz koordinátái
az alkalmazott vonatkoztatási rendszerben:
.

Jelölje V azt a fix vektort, amelyhez a forgást
fogjuk viszonyítani. V egy tetszőleges, b-re
merőleges vektor lehetne, legyen most a következő alakú:
V (sin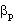 ,
0, -cos
,
0, -cos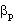 )
(7)
)
(7)
Most meghatározzuk azt a F szöget,
amellyel el kell forgatni az V vektort a b
körül ahhoz, hogy párhuzamos legyen a nn
vektorral, azaz a megfigyelő fényességmaximumot lásson.
Ennek feltétele, hogy

amelyből következik, hogy

Ismerve a F szög fokban kifejezett
értékét, már az O-C diagram pontjainak l-függése
is meghatározható:

Az egyszerűség kedvéért azonban praktikusabbnak
látszik a továbbiakban egy O-C'-vel jelölt értékkel
számolni, amelynek alakja:

Miután az O-C' vizsgálatából meghatározható
a kisbolygó tengelyének helyzete, egy olyan módszerhez
jutottunk, amely ezt csak az ekliptikai koordinátáktól
függően adja meg.
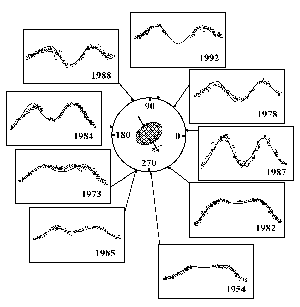
A 8. ábrán "elméleti" O-C' diagramokat
mutatunk be különböző forgástengely-irányok
esetében. Ezen diagramok egybevetéséből a következőket
állíthatjuk.

8. ábra. Elméleti O-C' diagramok hat forgástengely-irány
esetén
Az O-C' diagramok kezdő- és végértékének
különbsége mindig 1 (+1 prográd, -1 retrográd
esetben), ahogy ezt a forgás és keringés együttes
elképzelése is alátámasztja. Prográd
forgásnál ugyanis egy keringés alatt pont egy sziderikus
fordulattal látunk kevesebb szinodikus tengelyforgást, és
így az O-C' diagram érthetően egyre nagyobb értékeket
vesz föl. Retrográd forgásnál hasonlóan
jutunk az egyre korábbi O-C' mind korábbi, azaz egyre kisebb
értékeihez.
Másik fontos megállapítás,
hogy az elméleti O-C' diagram nagy 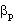 értékekre közel lineáris. Alacsonyabb tengelyállásoknál
pedig egyre inkább eltorzul az alakja; a pólus koordinátáit
jól jellemzi ez a megváltozott lefutás.
értékekre közel lineáris. Alacsonyabb tengelyállásoknál
pedig egyre inkább eltorzul az alakja; a pólus koordinátáit
jól jellemzi ez a megváltozott lefutás.
A későbbiekben ily módon tudjuk majd
meghatározni a forgástengely helyzetét és a
forgási periódust. Gyakorlati megfigyelések esetében
az O-C' pontok tapasztalat szerint csak egyetlen (monoton növekedő,
vagy monoton csökkenő) esetben közelítik meg a
lineáris föltételezést: akkor, amikor a pontok
meghatározásakor használt periódusérték
a valódi sziderikus periódussal megegyezik. Minden más
esetben a diagram pontjai egyszerű szórást mutatnak.
Azonban a valós O-C' diagram még függhet
a kisbolygó alakjától. Hogy ezt megszüntessük,
meghatározhatjuk az elméleti diagram deriváltját,
valamint a megfigyelt pontokból számolható meredekséget.
Ezzel a módszerrel az összefüggés közel független
a kisbolygó alakjától is, hiszen így már
csak az a föltételezés áll, hogy két szomszédos
O-C' pont között nem változik a fényességmaximum
sziderikus forgási fázisa.
A (9)-es differenciálásával kapjuk,
hogy
,
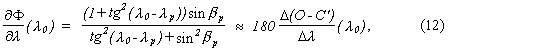
ahol 0 végigfut a megfigyelési pontok ekliptikai hosszúság-értékein.
Ezzel a deriválással megszüntettük az O-C diagram
értelmének epochafüggését is. (A levezetésben
a V vektor szimbolizálta ezt a referenciaállapotot.
Ez a vektor konstansként hozzáadódik a F
szög értékeihez, de a differenciálásnál
kiesik.)
1. Numerikus módszerrel meghatározzuk azt a periódust,
amelyre az O-C' - l diagram ±1/180 meredekségű
lineáris illeszkedése a legjobb. Első közelítésben
ezt a periódust fogadjuk el sziderikus periódusnak. (Ez a
periódus már legalább 10-6
napra pontos.)
2. Az így előállított grafikon lefutásából
azonnal adódik a forgás iránya.
3.  változtatásával
és a (12) összefüggés alkalmazásával
minimalizáljuk a számított
változtatásával
és a (12) összefüggés alkalmazásával
minimalizáljuk a számított 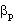 értékek szórását. A legjobb illeszkedésből
adódik
értékek szórását. A legjobb illeszkedésből
adódik  értéke.
értéke.
4. Az O-C' előállításakor használt
periódus kis mértékű változtatásával
is minimalizáljuk 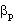 szórását. Az így kapott periódust fogadjuk
el végső sziderikus periódusnak, míg a kapott
szórását. Az így kapott periódust fogadjuk
el végső sziderikus periódusnak, míg a kapott 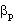 értéket a pólus második koordinátájának.
Előjele a 2. lépés során már adódott.
értéket a pólus második koordinátájának.
Előjele a 2. lépés során már adódott.
5. A 3. és 4. lépések iteratív ismétlése
addig, amíg az adódó új póluskoordináták
különbsége a régiektől egy küszöbérték
(5o) alá nem csökken. Így
végeredényben meghatároztuk a forgásvektort.
4.4. A módszer tesztelése
A módszert számítógépes modellkísérletekkel
és tesztobjektumok alapján is teszteltük. Számítógépes
analízisünk fő célja az volt, hogy bebizonyítsuk:
akorábbi tapasztalatokkal ellentétben az epocha-alapú
módszerek is ugyanolyan jól megadják a pólus
hosszúságát, mint az amplitúdó-alapúak.
Ezért a következő algoritmust hajtottuk végre:
1. Definiáltunk egy forgástengelyt véletlen  és adott
és adott 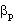 paraméterekkel. Hat véletlenül megválasztott
égi helyzetben kiszámítottuk az O-C' értékét
a (9) alapján.
paraméterekkel. Hat véletlenül megválasztott
égi helyzetben kiszámítottuk az O-C' értékét
a (9) alapján.
2. s szórású, Gauss
eloszlású zajjal (analógia: a maximumidőpontok
meghatározásának előre definiált hibáival)
terheltük az 1. pont által adott O-C' adatokat.
3. Ezekből a "megfigyelésekből" újraszámoltuk
a pólus helyzetét. Ezt összehasonlítottuk az
ismert, eredeti helyzettel.
4. Az 1-3. pontokat százszor megismételtük, azonos
s értékkel számolva. A
modellezési szériát akkor minősítettük
jónak, ha 100 esetből legalább 67 alkalommal a pólus
hosszúsága 5 (10) fokon belüli egyezésben volt
a "valósággal".
5. A s értéket szisztematikusan
növelve megismételtük az 1-4. pontokat. Az adott 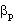 szélességhez megengedhető maximális extrémum-meghatározási
hibának azt a legnagyobb s értéket
minősítettük, amely még jó modellezési
sorozatot szolgáltatott.
szélességhez megengedhető maximális extrémum-meghatározási
hibának azt a legnagyobb s értéket
minősítettük, amely még jó modellezési
sorozatot szolgáltatott.
6. A 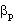 értékét is változtatva, ily módon tudtuk
meghatározni az adott szélességű tengely esetére
a megengedhető bizonytalanságokat, ami az extrémumok
meghatározását illeti.
értékét is változtatva, ily módon tudtuk
meghatározni az adott szélességű tengely esetére
a megengedhető bizonytalanságokat, ami az extrémumok
meghatározását illeti.
Az így kapott hibák, amint azt a 9. ábra mutatja,
2-5% körüliek. Az is jól látszik, hogy az alacsonyan
inklinált tengelyek esetében ugrásszerűen nő
az egyedi pontok megengedhető hibája, azaz, a módszer
pontos alkalmazhatósága.
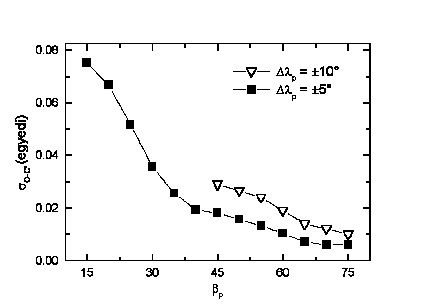 9. ábra. Az O-C' pontok maximálisan megengedhető
hibái a ±5°, ill. ±10° pontosságú
pólushosszúság meghatározáshoz, különböző
pólusszélességek mellett.
9. ábra. Az O-C' pontok maximálisan megengedhető
hibái a ±5°, ill. ±10° pontosságú
pólushosszúság meghatározáshoz, különböző
pólusszélességek mellett.
A fentebb említett 2-5% bizonytalansági paraméter
maximálja a két minimumhely közötti forgási
fázisbeli eltérést. Vezessük be ugyanis a fénygörbére
jellemző minimum deviancia fogalmát, amely a két minimum
közötti forgási fázis 0,5-től való
eltérése. (Ideális esetben, pl. szabályos ellipszoid
fénygörbéjére, ez 0.) Ezzel a paraméterrel
megfogalmazva azt mondhatjuk, hogy az O-C eljárás akkor alkalmazható,
ha a fénygörbék minimum devianciája 0,02-0,05
alatt van. Az eddig ismert 400 fénygörbe nagy hányadára
jellemző, hogy eleget tesznek ennek a megszorításnak.
Kivételek persze minden szabály alól vannak; saját
megfigyeléseink között is tudunk olyan példát
mutatni (852 Wladilena), amelyre a fönt adott kritérium nem
teljesül.
Így tehát megmutattuk, hogy módszerünkkel
az 5-10 fokos pólus-hosszúsági bizonytalanság
elérése sem reménytelen. (4-6 perces pontosságú
extrémum-meghatározás mellett.) Ez a tény a
tesztobjektumok illesztésekor is meggyőzően bizonyosodott.
A módszer hatékonyságának
szemléltetésére bemutatjuk a 201 Penelope részletes
analízisét. A 10. ábrán láthatjuk a 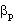 -
- paramétertérben a hibafüggvény felület-térképét.
(A vízszintes tengely ábrázolja a pólus szabadon
változó hosszúságát, a függőleges
tengely a szélességét, míg a színezés
az illesztés szórásnégyzetére jellemző.)
Jól látható, hogy csak egy megoldás adódik
a pólusra, és hogy ez a minimum a paramétertérben
igen jól definiált. A pontosság szemléltetésére
bemutatjuk ennek a három dimenziós grafikonnak a keresztmetszeteit
is,
paramétertérben a hibafüggvény felület-térképét.
(A vízszintes tengely ábrázolja a pólus szabadon
változó hosszúságát, a függőleges
tengely a szélességét, míg a színezés
az illesztés szórásnégyzetére jellemző.)
Jól látható, hogy csak egy megoldás adódik
a pólusra, és hogy ez a minimum a paramétertérben
igen jól definiált. A pontosság szemléltetésére
bemutatjuk ennek a három dimenziós grafikonnak a keresztmetszeteit
is, 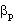 és
és  irányban. Ezek a grafikonok jól szemléltetik, hogy
a pólus koordinátái viszonylag elfogadható
hibával (±5-10 fok) megbízhatóan számíthatóak
az új módszer alapján.
irányban. Ezek a grafikonok jól szemléltetik, hogy
a pólus koordinátái viszonylag elfogadható
hibával (±5-10 fok) megbízhatóan számíthatóak
az új módszer alapján.
 10. ábra. A 201 Penelope szórásnégyzet-térképe
10. ábra. A 201 Penelope szórásnégyzet-térképe
Tesztobjektumaink kiválasztásakor a kritérium az
volt, hogy egymással jól egyező modellek szerepeljenek
a szakirodalomban.
 11. ábra. A 10. ábra globális minimumán
keresztülhaladó metszetek.
11. ábra. A 10. ábra globális minimumán
keresztülhaladó metszetek.
A 4. táblázatban közöljük
a teszt eredményét. Az oszlopok sorrendben a forgási
periódusokat (napban kifejezve), a pólus két koordinátáját,
a forgás irányát (P: prográd, R: retrográd),
ill. a megfelelő referenciát tüntetik fel. Mivel az
előző eljárások eredménye nem meghatározott
módon többértelmű, így érthető,
ha ugyanabban a dolgozatban több lehetséges modellt is közölnek
a szerzők. Az általunk kifejlesztett módszer csak
a pólus hosszúságában meghatározatlan,
így mi a lehetséges két tengelyhelyzet első
koordinátáját összevont formában közöljük.
A fölhasznált fénygörbék az Asteroid Photometric
Catalogue (Lagerkvist et al. 1997) adatsorából származnak;
az egyedi fénygörbék referenciáit az irodalomjegyzékben
soroljuk föl.
Az alábbiakban részletesen összevetjük
eredményeinket a korábbiakkal.
20 Massalia
A forgási periódust 0.0000004 nap pontossággal
sikerült meghatároznunk. A póluskoordináták
jó egyezést mutatnak McCheyne et al. (1985), Magnusson (1986)
és Dotto et al. (1995) eredményeivel, míg a pólus
szélessége jelentősen eltérő, különös
tekintettel a két utóbbi dolgozatra. A forgás iránya
minden előző meghatározással egyetértésben
prográdnak bizonyult.
21 Lutetia
Négy oppozíció adatsora áll rendelkezésünkre.
A forgási periódust először Lupishko & Velichko
(1987) határozta meg, míg Lupishko et al. (1987) csak alakmodellt
közöl. Mind az említett munka, mind Micha owski (1993)
két lehetséges koordináta-párt határozott
meg a pólusra. Később De Angelis (1995) és
Michalowski (1996) erősen eltérő periódust
kapott. Számításaink eredménye jó összhangban
van az előző eredményekkel. Az 1996-ban publikált
forgási periódust nem erősíthetjük meg.
43 Ariadne
Detal et al. (1994) közöltek átfogó tanulmányt
erről az aszteroidáról, akik a kérdéses
dolgozatban négy különböző modellező
eljárást hasonlítottak össze. Az általunk
meghatározott forgásvektor igen jó egyezésben
van ezekkel az adatokkal.
79 Eurynome
Az általunk számított forgási periódus
és a póluskoordináták jól egyeznek az
előző publikációk értékeivel,
azonban a korábbi modellekkel szemben retrográd forgást
határoztunk meg.
201 Penelope
A forgási periódus ennél a kisbolygónál
adódott a legpontosabban (0.1561441 ±0.0000003 nap). Az általunk
meghatározott modell minden paraméterét tekintve egyezik
az előzőekkel.
532 Herculina
Ennek a kisbolygónak igen érdekes a fényváltozása
(l. 6. ábra). Míg sokszor két maximum figyelhető
meg egy forgás alatt, bizonyos helyzetekben a fénygörbe
csak egyetlen maximumot mutat. Micha owski (1996) egy olyan háromtengelyű
ellipszoid modellel írta le ezt a jelenséget, melynek kistengelye
és forgástengelye nem esik egybe, hanem 7 fokkal hajlanak
egymáshoz. Miután az általunk bemutatott eljárás
gyakorlatilag független a kisbolygó alakjától,
így egyszerűbb modellünk is jó egyezésben
van Micha owski (1993) és Micha owski (1995) eredményeivel.
642 Hector
Az előző modellek szintén Detal et al. (1994)
dolgozatából származnak. A forgásvektor teljes
leírása lényegében megegyezik saját
eredményeinkkel.
Összességében elmondhatjuk, hogy az
általunk használt eljárás teljes mértékben
összevethető az előző számítások
végeredményével. A forgási periódust
minden eddiginél pontosabban tudtuk meghatározni. A forgásirány
(P vagy R) meghatározása az eljárás természetéből
adódóan gyakorlatilag egyértelmű, míg
ez korántsem mondható el az előző számításokról
(l. 79 Eurynome, 532 Herculina). Másik előnye az eljárásnak,
hogy csak egy értéket szolgáltat a pólus szélességére,
így az erősen különböző szélességekkel
jellemzett korábbi modellpárok közül csak egyet
támogat. A fő hátrány az, hogy a pólus
hosszúságának meghatározása még
mindig nem teljesen egyértelmű. Ez a módszer két
lehetséges hosszúságát adja meg a forgástengelynek;
ezek pontosan 180 -ban különböznek egymástól.
4.5. Megfigyelési eredményeinkből
Az elmúlt két évben összesen 20 kisbolygó
fotometriáját végeztük. Ennek keretében
29 éjszakán 2 műszeregyüttessel 2371 pontot tudtunk
fölvenni. A mérések részletezése a 5.
táblázatban található.
Az objektumválasztás szempontjait a használt
műszerek jellege erősen meghatározta. Az 500-as sorszámnál
kisebb, általában fényes és többé-kevésbé
észlelt kisbolygók kutatását Szegedről
végeztük, míg az 500-nál nagyobb sorszámot
viselő aszteroidákat Piszkéstetőről
mértük. Különösen a szegedi programnak volt
célkitűzése az, hogy a megfigyelt kisbolygóknak
ne legyen előző modellje, de a mi méréseink
alapján már modellt is közölhessünk. Ezzel
a műszerrel végeztük el az 52, a 73 és a 316 kisbolygók
fotometriáját.
Az alábbiakban bemutatjuk a mérései
eredményeket egyedi objektumokra lebontva.
52 Europa
Ezt a kisbolygót P. Denchev bolgár csillagásszal
ugyanazon az éjszakán mértük a véletlennek
köszönhetően. A két fénygörbe (12.
ábra) láthatóan teljesen együtt halad, ami mutatja,
hogy a JATE Béke-épületének tetejéről
végzett mérések teljesen megállják helyüket
nemzetközi összevetésben is. Ezen mérések
alapján a kisbolygó előző, meglehetősen
bizonytalan modellje nagy mértékben pontosítható.
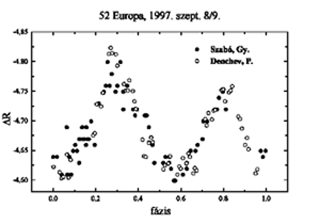 12. ábra. Az 52 Europa kompozit fénygörbéje
12. ábra. Az 52 Europa kompozit fénygörbéje
73 Klytia
Jelenlegi adatsorunk nem elég a háromtengelyű ellipszoid
modelljéhez. Egy hozzávetőleges modellt táblázatunkban
adunk meg. A 13. ábrán látható kompozit fénygörbe
a négy éjszaka adatait együtt ábrázolja.
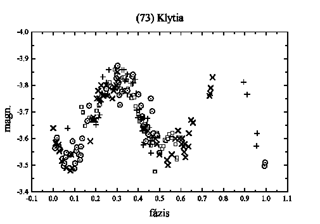 13. ábra. A 73 Klytia kompozit fénygörbéje.
Jelek: o - 97.02.20.,+ 97.02.22.,
¤ - 97.02.23., ´ - 97.03.02.
13. ábra. A 73 Klytia kompozit fénygörbéje.
Jelek: o - 97.02.20.,+ 97.02.22.,
¤ - 97.02.23., ´ - 97.03.02.
288 Glauke
Piszkéstetői méréseink alapján 5
óra alatt fényváltozása nem haladta meg a
fénygörbe szórását (±0.01 magn.).
316 Geometria
Szegedi méréseink alapján 1997-es oppozíciójában
minden eddiginél kisebb, 0,08 magnitúdós volt az amplitúdója.
409 Aspasia
A 168±8 km-es kisbolygó fotometriáját B,V,R,I
szűrőkön keresztül végeztük, tíz
éjszakán 597 pontot fölvéve. Az adatok földolgozása
jelenleg folyamatban van; eddigi eredményeinket a következőekben
foglalhatjuk össze:
A szinodikus periódus 9,21±0,04 óra,
míg az amplitúdó 0,12 és 0,30 magnitúdó
között változik. A 14. ábrán egy jellegzetes
fénygörbét mutatunk be, míg a 15. ábrán
a színindex változásait tüntetjük föl.
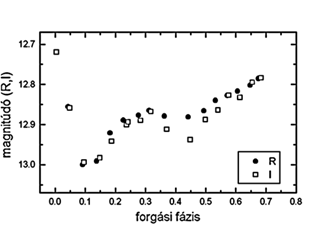 14. ábra. Az Aspasia fénygörbéje 1998
szeptember 24-én,
R és I szűrőkkel
14. ábra. Az Aspasia fénygörbéje 1998
szeptember 24-én,
R és I szűrőkkel
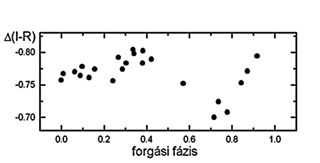 15. ábra. A 409 Aspasia I-R színindexe. Kompozit
diagram (98.09.21. és 24.)
15. ábra. A 409 Aspasia I-R színindexe. Kompozit
diagram (98.09.21. és 24.)
A fénygörbe legfontosabb jellemzői (amplitúdó,
alak, minimumok mélysége, általában a lefutása)
éjszakáról éjszakára jelentős
változásokat mutatnak. Emiatt az egyéb paramétereknél
relatíve pontosabban mérhető amplitúdó
modulációin keresztül vizsgáltuk a kisbolygót.
Eredményeink szerint az amplitúdó periodikusan ingadozik,
mégpedig 1,706±0,002 napos ciklushosszal (16. ábra).
Mivel az amplitúdó (egy adott kisbolygóra) eddig ellenpélda
nélkül csak az aspecttel függ össze (l. AM módszerek),
ezért arra kell következtetnünk, hogy az amplitúdó
periodikus változását az aspect periodikus változása
okozza. Ennek legvalószínűbb magyarázata a precesszió
föltételezése.
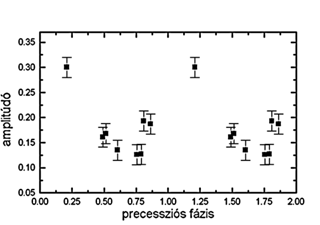 16. ábra. Az amplitúdó változásának
fázisdiagramja
16. ábra. Az amplitúdó változásának
fázisdiagramja
A viszonylag kicsi amplitúdók (<0,3m)
alapján az alak nem nagyon tér el a gömbtől,
egy "átlagos" alakmodell egy 1,3±0,1:1,1±0,07:1 tengelyarányú
ellipszoiddal adható meg.
A precesszió nem adódhat egy hold gravitációs
forgatónyomatékából. Ekkor ui. a kísérő
m tömege, a pálya a fél nagytengelye,
i inklinációja, valamint az W
és w szögsebességű
precesszió és tengelyforgás között
fönnáll (Binzel, 1985):

(G a gravitációs állandó). A (13)-ban szereplő
g állandó az alábbi módon
adódik a Qi
(i=1, 2, 3) fő tehetetlenségi nyomatékokból:
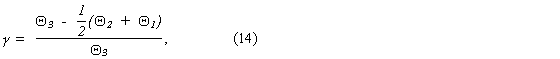
ahol Q3 >
Q2 > Q1.
(13) alapján kiszámítva a kísér_
minimális tömegét (0 inklinációjú
pályán, a fél nagytengely az Aspasia átlagos
sugara) is legalább 1000 km nagyságrendű kísérőt
kell föltételeznünk ahhoz, hogy ilyen precessziót
hozzon létre. Ez nyilvánvalóan lehetetlenség;
ezért az aspect változását a szabad precessziónak
kell tulajdonítanunk. Ennek periódusára az ismert
képlet (Landau & Lifsic 1988) alapján,
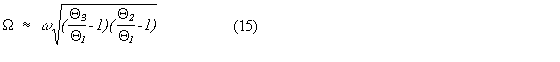
1,3:1,13:1 tengelyarányú ellipszoidra, 9,2 órás
forgási sebességre 1,77 nap adódik. Ez az érték
jó összhangban van a megfigyelésekkel, így joggal
föltételezhető e jelenség megfigyelése.
Általánosan elfogadott nézet, hogy
a szabad precesszió a kisbolygók világában
akkor jön létre, mikor két aszteroida ütközésekor
az impulzusmomentum vektora kibillen a fő tehetetlenségi
tengelyből. A föltételezett ütközés
energiáját a következőképpen becsültük:
A tehetetlenségi nyomatékot adott sűrűségű,
170 km sugarú gömbre számítottuk. Az ütközés
energiáját alulról becsüljük, ha a jelenlegi
összes impulzusmomentumhoz tartozó energiából
kivonjuk a forgás energiáját. (A precessziós
tengely és a forgástengely által bezárt szöget
25 fokosnak becsültük a fénygörbék alapján.)
Végeredményképpen az ütközési energiára
6,1±1,5 102 J/kg értéket
kaptunk, amit a jelenleg elfogadott elméletek szerint egy 168 km
átmérőjű kisbolygónak még biztosan
ki kell bírnia törés nélkül. Ugyanakkor
nyilvánvalóan alábecsültük a becsapódást,
hiszen a forgásvektort, a pályaelemeket, a mechanikai, ill.
a kémiai jellemzőket megváltoztató energiát
nem vettük figyelembe.
Az általunk becsült ütközési
energia szerint egy, az Aspasiaval azonos sűrűségű,
50 km átmérőjű test 0,21 km/s-os, 30 km átmérőjű
0,46 km/s-os ütközési sebesség mellett képes
ekkora energiát közölni, ha tökéletesen rugalmas
az ütközés. A rugalmatlan ütközés esetében,
beleszámítva az egyéb energiaveszteségeket,
a 0,7±1,5 km/s-os ütközési sebességek reálisak,
30-50 km átmérőjű ütköző testekre.
A többszín-fotometriai megfigyeléseken
jól látható a színindex változása
is. (15. ábra). Elkékülést tapasztalhatunk egy
adott forgási fázisnál, ami idegen anyag (=eltérő
színű folt) jelenlétére utal a felszínen.
Zappala et al. (1985) már megemlítette korábban ezt
a lehetőséget a megfigyelt fénygörbe-változások
egyik lehetséges okaként, azonban részletes többszín-fotometria
azóta sem készült. Az ütközés összetapadás
koncepciójának természetes következménye
az albedójában különböző régió
a kisbolygó felületén, tehát két oldalról
is konzisztens képet kaphatnuk a 409 Aspasia fentebb részletezett
modelljével. A minimum előtti elhalványulás
egyes éjszakákon igen gyorsnak bizonyult; de ezt a jelenséget
már korábbi mérések alkalmával is megfigyelték.
683 Lanzia
Előző fotometriai adatsorai az 1979, 1982, 1983-1984,
1987-es oppozíciókból származnak (Carlsson
& Lagerkvist 1981, Weidenschilling et al. 1990). 1998 december 12-16.
között 4,61 órás periódussal 0,125 magnitúdós
fényváltozást figyeltünk meg. A kompozit diagramot
a 17. ábrán mutatjuk be.
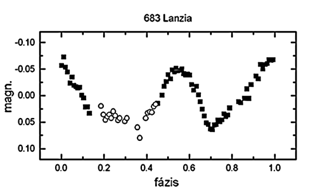 17. ábra. A 683 Lanzia kompozit fázisdiagramja. Alkalmazott
jelek:
telt négyzet - 98.12.14., üres kör - 98.12.16.
Modellezését AM-módszerrel végeztük, így
115:105:100 tengelyarányokkal jellemzett ellipszoidot határoztunk
meg, 19/199±20 fokos hosszúságú, 78±10
fokos szélességű forgástengellyel. Az illesztett
amplitúdó-változást a 18. ábrán
közöljük.
17. ábra. A 683 Lanzia kompozit fázisdiagramja. Alkalmazott
jelek:
telt négyzet - 98.12.14., üres kör - 98.12.16.
Modellezését AM-módszerrel végeztük, így
115:105:100 tengelyarányokkal jellemzett ellipszoidot határoztunk
meg, 19/199±20 fokos hosszúságú, 78±10
fokos szélességű forgástengellyel. Az illesztett
amplitúdó-változást a 18. ábrán
közöljük.
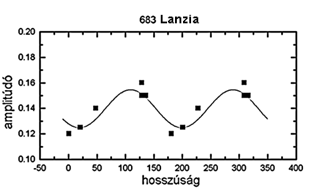 18. ábra. A 683 hosszúság-amplitúdó
függése az illesztett görbével
18. ábra. A 683 hosszúság-amplitúdó
függése az illesztett görbével
792 Metcalfia
A fényváltozás alapvető paramétereit
először Carlsson & Lagerkvist (1981) határozta meg
1979-ben. Ekkor 9,22 órás periódusú és
0,64 magnitúdós amplitúdójú fényváltozást
detektáltak. Saját méréseink (9,19±0.01
óra, 0,76±0,02 magnitúdó) ezzel jó összhangban
vannak; a nagyobb amplitúdó geometriai okokra vezethető
vissza. A fénygörbe alakja meglehetősen szokatlan, mivel
a minimumok élesek és igen rövid ideig tartanak. Az
eddigi két mérési sorozatnak köszönhetően
ez a kisbolygó a következő oppozíció után
már modellezhető lesz. A 19. ábrán bemutatott
kompozit diagramunk nullfázisa JD 2451110,2050.
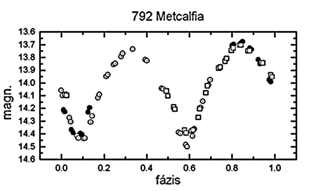 19. ábra. A 792 Metcalfia fázisdiagramja. Jelek:
üres négyzet - 98.10.22.,
pontozott kör - 98.10.23., telt kör - 98.10.26.
19. ábra. A 792 Metcalfia fázisdiagramja. Jelek:
üres négyzet - 98.10.22.,
pontozott kör - 98.10.23., telt kör - 98.10.26.
852 Wladilena
Három előző fotometriája ismeretes az 1977,
1982, 1993-as évekből. (Tedesco 1979, Di Martino & Cacciatori
1984, De Angelis & Mottola 1995.) 6,42 órás forgása
alatt 0,32 magnitúdós fényváltozást
mutattunk ki, amely alig különbözik az előző
fotometriák eredményétől (20. ábra).
 20. ábra. A 852 Wladilena fázisdiagramja. Jelek:
telt kör - 98.12.12.,
pontozott kör - 98.12.14., telt négyzet - 98.12.16.
20. ábra. A 852 Wladilena fázisdiagramja. Jelek:
telt kör - 98.12.12.,
pontozott kör - 98.12.14., telt négyzet - 98.12.16.
Az előző mérésekhez tartozó hosszúságok
szerencsétlen eloszlása miatt AM-modellezés nem végezhető.
Azt azonban meg lehet állapítani, hogy a pólus a 170/350
fokos hosszúság irányába mutat, és a
tengely inklinációja biztosan 60 fok fölötti. A
továbbiakban sajnos O-C modellezés nem lesz lehetséges,
mert a minimumdeviancia (4.4. pont) 0,17.
1089 Tama
Ez a kisbolygó meglehetősen kis méretű,
14,1±0,8 km. A megfigyelt fényváltozás (21.
ábra) amplitúdója igen alacsony volt, 0,025 magn.
A szinodikus periódus gyaníthatóan 8,8±1 óra.
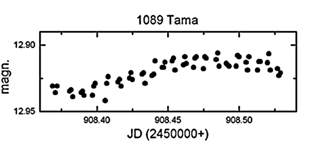 21. ábra. Az 1089 Tama fénygörbéje
21. ábra. Az 1089 Tama fénygörbéje
1452 Hunnia
Ezt a Kulin György által fölfedezett kisbolygót
is mi mértük először. 17,2±0,1 órás
szinodikus periódusa igen hosszúnak nevezhető; ez
0,34 magnitúdós amplitúdóval társul.
Az egy nap eltéréssel végzett mérések
során azonos összehasonlítót használtunk,
így a két észlelt minimum közötti 0,11 magn.
fényességkülönbség nem az aspect változásának,
hanem a két minimum tényleges különbözőségének
az eredménye (22. ábra).
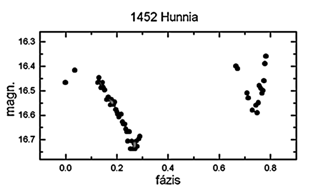 22. ábra. Az 1452 Hunnia kompozit fénygörbéje
22. ábra. Az 1452 Hunnia kompozit fénygörbéje
1508 Kemi
Holliday (1995) már végzett egy mérési
sorozatot, de forgási periódust nem határozott meg.
Saját megfigyeléseink szerint egy forgás 9,15±0,03
óra alatt történik, ami alatt 0,52±0,01 magnitúdós
fényváltozás mérhető (23. ábra).
 23. ábra. Az 1508 Kemi fázisdiagramja. Jelek:ópontozott
kör - 98.10.22.,
telt kör - 98.10.26.
23. ábra. Az 1508 Kemi fázisdiagramja. Jelek:ópontozott
kör - 98.10.22.,
telt kör - 98.10.26.
1604 Tombaugh
Előző fotometriái: 1975 (Lagerkvist 1978) és
1984 (Binzel 1987). Bár az 1975-ös fénygörbe szórása
nagy, Binzel pedig mindössze 16 pontot közöl, AM-módszerrel
modellezni tudtuk forgását. Az alakot egy a/b=1,16±0,10,
b/c=1,05±0,05 tengelyarányú ellipszoiddal jellemeztük,
míg aszámított forgásvektor:
 =3/183±10o,
=3/183±10o, 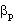 =60±15o
.
=60±15o
.
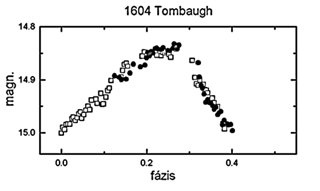 24. ábra. Az 1604 Tombaugh fázisdiagramja. Alkalmazott
jelek:
nyílt négyzet - 98.01.04., telt kör - 98.01.05.
24. ábra. Az 1604 Tombaugh fázisdiagramja. Alkalmazott
jelek:
nyílt négyzet - 98.01.04., telt kör - 98.01.05.
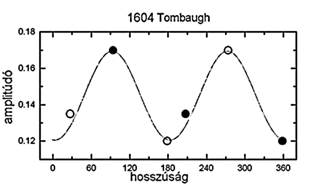 25. ábra. Az 1604 hosszúság-amplitúdó
függése az illesztett görbével
25. ábra. Az 1604 hosszúság-amplitúdó
függése az illesztett görbével
1627 Ivar
1985 és 1990 között három fotometriai adatsor
és egy radarmérés született erről az aszteroidáról
(Hahn et al. 1989, Velichko et al. 1990, Hoffmann & Geyer 1990, Ostro
et al. 1990). Méréseinket 1998 december 14-16. között
végeztük, és ezek alapján 0,77 magnitúdós
amplitúdót állapítottunk meg, 4,797 órás
periódussal (26. ábra).Az előző mérésekkel
összevetve AM-módszerű modellezést vittünk
véghez (20. ábra), melynek eredményeképpen
az alakot a/b=1,75, b/c= 1,23 arányokkal bíró ellipszoid
képében határoztuk meg.
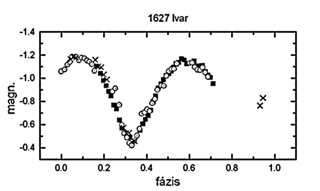 26. ábra. Az 1627 Ivar fázisdiagramja. Kör ponttal:
98.12.15.,
négyzet: 98.12.14., x: 98.12.16.
26. ábra. Az 1627 Ivar fázisdiagramja. Kör ponttal:
98.12.15.,
négyzet: 98.12.14., x: 98.12.16.
A forgásvektor koordinátái (325, 17). Az amplitúdók
illesztését a 27. ábrán mutatjuk be. A mért
és illesztett amplitúdók viszonylag nagy eltérése
a tengely alacsony és a pálya nagy inklinációjának
együttes eredménye. Az ekliptikától jelentősen
kiemelkedő pozíciókban ugyanis az aspect erősen
b-függő. Számításaink során
ezt a jelenséget természetesen számba vettük;
azonban két független és egy függő változó
ábrázolása szinte reménytelen feladat, ezért
az illesztett görbét 0 pályainklinációra
számítottuk, eliminálva ezzel az illesztés
egyik dimenzióját.
 27. ábra. Az 1627 Ivar megfigyelt amplitúdói
és a modell illesztése
27. ábra. Az 1627 Ivar megfigyelt amplitúdói
és a modell illesztése
1727 Mette
Erről a kisbolygóról készült az első,
immár történelmi jelentőségűkisbolygós
fotometria, még 1932-ben. Az előző adatsort kiegészítve
méréseinkkel, pontos modellt tudtunk adni a kisbolygóra:  = 120/300±10o,
= 120/300±10o, 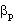 =43±15o,
a/b=1,91±0,10, b/c=1,55±0,10.
=43±15o,
a/b=1,91±0,10, b/c=1,55±0,10.
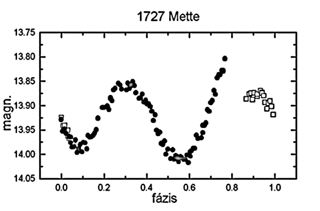 28. ábra. Az 1727 Mette fázisdiagramja. Jelek: nyílt
négyzet - 98.02.26.,
telt kör - 98.02.27.
28. ábra. Az 1727 Mette fázisdiagramja. Jelek: nyílt
négyzet - 98.02.26.,
telt kör - 98.02.27.
 29. ábra. Az 1727 hosszúság-amplitúdó
összefüggése az illesztett görbével
29. ábra. Az 1727 hosszúság-amplitúdó
összefüggése az illesztett görbével
1865 Cerberus
Ezt a Kohoutek által fölfedezett kisbolygót úgy
tartják számon, mint az egyiklegnagyobb fényváltozást
produkáló aszteroidát. Első fotometriája
alkalmával (Harris & Young 1989) 2 magnitúdós
fényváltozás volt tapasztalható. Saját,
158 pontból álló R szűrős mérésünk
alatt még nagyobb, 2,3±0,1 magnitúdós változást
tapasztaltunk. A szimmetrikus fénygörbe alapján valószínűsíthető,
hogy egy igen elnyúlt (a/b legalább 8!) alak forgása
okozza a megfigyelt változást. Lehet, hogy egy kisbolygók
közötti ütközés alkalmával letört
szilánkkal állunk szemben az 1865 Cerberus személyében.
Az igen nagy látszó sajátmozgás miatt (4" percenként)
2 perces integrációs időket alkalmaztunk. A mérés
közben nagy élmény volt a monitoron követni a fényváltozást,
mivel a maximumban átlagosan fényes (16 magnitúdó
körüli) kisbolygó minimumban szinte eltűnt a CCD-képekről!
Kompozit diagramunk nulla fázisa JD 2451113,5000 (30. ábra).
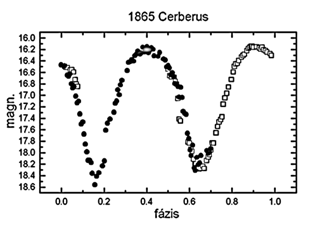 30. ábra. Az 1865 Cerberus kompozit fénygörbéje.
Jelek:
nyílt négyzet - 98.10.23., telt kör - 98.10.26.
30. ábra. Az 1865 Cerberus kompozit fénygörbéje.
Jelek:
nyílt négyzet - 98.10.23., telt kör - 98.10.26.
2415 Ganesa
Első fotometriát végeztünk. 0,15 magnitúdós
amplitúdója és 6,86±0,25 órás
forgási periódusa szokványosnak mondható.
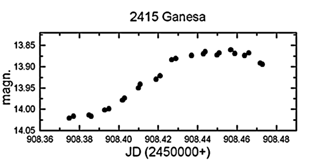 31. ábra. A 2415 Gneisa fénygörbéje
31. ábra. A 2415 Gneisa fénygörbéje
9262 1973 RF
Habár a kisbolygó átmérője 20 km,
méretét meghazudtolóan kicsi az amplitúdója,
0,08±0,015 magn. Első fotometriánk alapján
periódusát 8,5±0,5 órára tehetjük.
 33. ábra. A 9262 1973 RF fénygörbéje
33. ábra. A 9262 1973 RF fénygörbéje
1989 UR
Ennek a kisbolygónak is első fotometriáját
végeztük. A megfigyelési eredményekből
megbízhatóan kimutatható, hogy az átlagfényesség
0,15 magnitúdóval változott méréseink
alatt. Ezen kívül a fénygörbe erősen sugall
egy kicsit több, mint 1 órányi periódusú
fényváltozást is. Ennek biztos alátámasztásához
azonban több éjszakára terjedő adatsorra lenne
szükség.
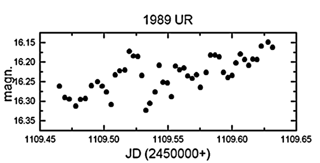 33. ábra. Az1989 UR felű földsúroló
fénygörbéje
33. ábra. Az1989 UR felű földsúroló
fénygörbéje
1998 FM5
Ezt a földsúroló kisbolygót a NEAT csoport
fedezte fel 1998. március 24-én. Nagy látszó
sajátmozgása miatt egy perces expozíciókat
kellett alkalmaznunk. A fényváltozás amplitúdója
0,61 magnitúdó, ami szokványos érték
a hasonló kisbolygók között. A szinodikus periódus
10±1 óra.
 34. ábra. Az 1998 FM5 fénygörbéje
34. ábra. Az 1998 FM5 fénygörbéje
1998 PG
Három éjszakáról van adatsorunk. Két
periódusú fénygörbét kaptunk, melynek
Fourier-analízisével 1,25 illetve 6,4 órás
forgási periódusokat állapítottunk meg. Az
adatok részletes analízise Petr Pravec (Ondrejov Obszervatórium,
Csehország) irányításával jelenleg folyamatban
van. Véleményünk szerint azonban e kisbolygó
esetében is szabad precessziót kell föltételeznünk,
a 409 Aspasiánál már részletezett okok miatt.
Ebben az esetben egy ilyen mértékű precesszió
kiváltásához legalább 1,5 J/kg -os ütközési
energiávl kell számolnunk. Mivel ez erősen alsó
becslés, kétséges, hogy az adott méretű
(kb. 2 km átmérőjű) kisbolygótest valóban
elszenvedte az ütközést. (U.i. ez az energia közel
van a 2 km-es kisbolygók törési küszöbéhez,
és a valódi energia nyilván 2x 5x nagyobb volt ennél.)
Ezért azt is el lehet képzelni, hogy az 1998 PG egy nagyobb
aszteroida ütközése során leszakadt darab. Ez esetben
a "szülőobjektum" ütközése nem történhetett
50 100 ezer évnél régebben, hiszen a szabad precesszió
jelensége ilyen időskálán megszűnik.
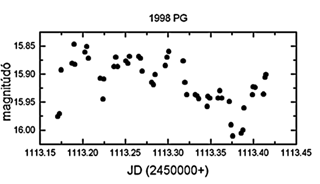 35. ábra. Az 1998 PG tipikus fényváltozása
(98.11.26.)
35. ábra. Az 1998 PG tipikus fényváltozása
(98.11.26.)
Egy jellegzetes fénygörbéjét
a 35. ábrán, míg a három éjszaka egyesítettfénygörbéjének
Fourier-spektrumát a 36. ábrán mutatjuk be.
 36. ábra. Az 1998 PG Fourier-spekruma
36. ábra. Az 1998 PG Fourier-spekruma
A 6. táblázatban összefoglaljuk a mért kisbolygók
általunk meghatározott fizikai paramétereit. Az oszlopok
rendre: kisbolygó sorszáma, szinodikus periódus órában
(±0,01-1 óra), sziderikus periódus napban (±0.0000007
nap), fényváltozás amplitúdója magnitúdóban
(±0,01), a pólus ekliptikai koordinátái (±10
), tengelyarányok a háromtengelyű ellipszoid-modellben
(±0,05). Teljes modellt csak két kisbolygóra tudtunk
megadni, ezek értékét az emeli, hogy a mi eredményeink
a legelsők az irodalomban. Az 52 Europa és 316 Geometria
szintén modellezhető megfigyeléseink segítségével,
de ez a munka T. Michalowski irányításával
folyik a Poznani Obszervatóriumban.
| Kisbolygó |
Psin (h) |
Psid (h) |
A (mag) |
 |
 |
a/b |
b/c |
| 52 |
5,24 |
* |
0,22 |
* |
* |
* |
* |
| 73 |
8,29 |
|
0,28 |
|
|
1,26 |
|
| 288 |
? |
|
? |
|
|
|
|
| 316 |
6,3 |
* |
0,08 |
* |
* |
* |
* |
| 409 |
9,2 és 40,9 |
|
0,12 és 0,3 |
|
|
1,18 |
1,1 |
| 638 |
4,61 |
|
0,125 |
19/199o |
78o |
1,1 |
1,05 |
| 792 |
9,19 |
|
0,76 |
|
|
|
|
| 852 |
6,42 |
|
0,32 |
170/350o |
>60o |
>1,35 |
|
| 1089 |
8,8 |
|
0,025 |
|
|
|
|
| 1452 |
17,2 |
|
0,34 |
|
|
|
|
| 1508 |
9,15 |
|
0,52 |
|
|
|
|
| 1604 |
6,19 |
|
0,17 |
3/183o |
60o |
1,16 |
1,05 |
| 1627 |
4,797 |
|
0,77 |
325o |
17o |
1,75 |
1,23 |
| 1727 |
3,22 |
0,1325948 |
0,15 |
120/30o |
43o |
1,91 |
1,55 |
| 1865 |
6,87 |
|
2,3 |
|
|
>8 |
|
| 2415 |
6,86 |
|
0,15 |
|
|
|
|
| 9262 |
8,5 |
|
0,08 |
|
|
|
|
| 1989 UR |
>20 és 1,07? |
|
>0,15 |
|
|
|
|
| 1998 FM5 |
10,0 |
|
0,60 |
|
|
|
|
| 1998 PG |
1,25 és 6,4 |
|
0,16 |
|
|
|
|
6. táblázat. A megfigyelt kisbolygók fizikai
paraméterei
![]() )
a ZPABP ekliptikai hosszúságával definiáljuk,
míg a pólus szélessége (
)
a ZPABP ekliptikai hosszúságával definiáljuk,
míg a pólus szélessége (![]() )
a minimális aspect nagysága (gyakorlatilag azt írja
le, hogy hány fokkal hajlik a forgástengely az ekliptikához).
)
a minimális aspect nagysága (gyakorlatilag azt írja
le, hogy hány fokkal hajlik a forgástengely az ekliptikához).