Next: Neutroncsillagok, fekete lyukak Up: Csillagfejlődési végállapotok Previous: Fehér törpék evolúciója
A ![]()
![]() -nél
nagyobb tömegű csillagok magjában a fúzió egészen a vasig
végbemegy
(lásd 2.3.2. fejezet). Az ilyen csillagmagok nem maradnak meg
stabil fehér törpe állapotban.
Amikor a mag sűrűsége eléri a
-nél
nagyobb tömegű csillagok magjában a fúzió egészen a vasig
végbemegy
(lásd 2.3.2. fejezet). Az ilyen csillagmagok nem maradnak meg
stabil fehér törpe állapotban.
Amikor a mag sűrűsége eléri a
![]() g/cm
g/cm![]() -t, hőmérséklete a
-t, hőmérséklete a
![]() K-t,
lehetővé válik a gyenge kölcsönhatás vezérelte inverz
béta-bomlás:
K-t,
lehetővé válik a gyenge kölcsönhatás vezérelte inverz
béta-bomlás:
A vasmag tömege a kollapszus pillanatában kb. a
Chandrasekhar-tömeg (1.4.2. fejezet), sugara
kb. 0,01 ![]() .
Az összeomlás időskálája a szabadesési időskála (2.1.2. fejezet),
kb. 1 s.
.
Az összeomlás időskálája a szabadesési időskála (2.1.2. fejezet),
kb. 1 s.
Az összeomló vasmagban a neutronizáció teljessé válik, azaz kb.
egy Chandrasekhar-tömegű neutrongömb
jön létre (neutroncsillag). A kollapszust a neutronok
elfajulása képes csak befolyásolni, kb.
![]() g/cm
g/cm![]() sűrűség elérésekor.
A neutronok elfajulásával a nyomás hirtelen megnő,
így a neutrongömb összeomlása lelassul, vagy megáll. A mag
feletti, nem elfajult gázból álló burok azonban továbbra is
szabadeséssel zuhan a magra, amelyet elérve visszapattan. A
visszapattanó
és a még befelé hulló rétegek ütközésénél nagy sűrűségű lökéshullám
alakul ki, amely
kifelé egyre növekvő sebességgel terjed. A lökéshullám felfűti és
ledobja a nagy tömegű
csillagburkot,
amely egy nagy (
sűrűség elérésekor.
A neutronok elfajulásával a nyomás hirtelen megnő,
így a neutrongömb összeomlása lelassul, vagy megáll. A mag
feletti, nem elfajult gázból álló burok azonban továbbra is
szabadeséssel zuhan a magra, amelyet elérve visszapattan. A
visszapattanó
és a még befelé hulló rétegek ütközésénél nagy sűrűségű lökéshullám
alakul ki, amely
kifelé egyre növekvő sebességgel terjed. A lökéshullám felfűti és
ledobja a nagy tömegű
csillagburkot,
amely egy nagy (
![]() km/s)
sebességgel táguló,
km/s)
sebességgel táguló, ![]() K kezdeti hőmérsékletű tűzgolyót
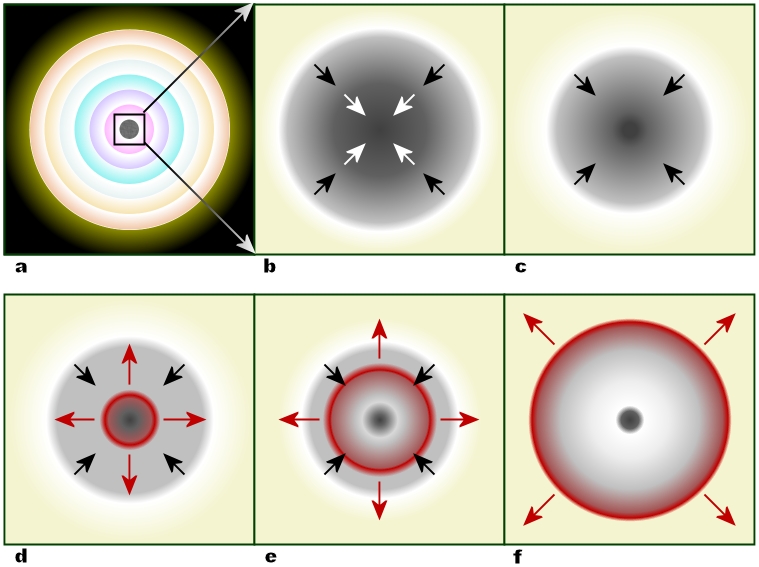
hoz létre. Ez a folyamat a szupernóva-robbanás (vázlatosan
lásd a 2.5. ábrán).
K kezdeti hőmérsékletű tűzgolyót
hoz létre. Ez a folyamat a szupernóva-robbanás (vázlatosan
lásd a 2.5. ábrán).
 |
A magkollapszus során felszabaduló gravitációs energia nagyságrendileg
A szupernóva-robbanásban keletkező táguló burokban az expanziós
sebesség arányos a középponttól
mért távolsággal (homológ tágulás):
![]() , ahol
, ahol
![]() a
táguló
burok maximális mérete,
a
táguló
burok maximális mérete,
![]() km/s ennek a rétegnek a tágulási sebessége.
km/s ennek a rétegnek a tágulási sebessége.
Ha a burok adiabatikusan tágulna, 1-2 hét alatt teljesen kihűlne.
A megfigyelések szerint azonban
a robbanás során nukleoszintézissel 56-os tömegszámú radioaktív
nikkel (![]() Ni) is
keletkezik.
Ez 6,1 nap felezési idővel 56-os tömegszámú kobalttá bomlik. A
Ni) is
keletkezik.
Ez 6,1 nap felezési idővel 56-os tömegszámú kobalttá bomlik. A ![]() Co szintén
radioaktív,
77,7 napos felezési idővel stabil vassá (
Co szintén
radioaktív,
77,7 napos felezési idővel stabil vassá (![]() Fe) alakul. A
Fe) alakul. A ![]() Ni -
Ni - ![]() Co -
Co - ![]() Fe
bomlási lánc miatti energiafelszabadulás belülről fűti a
ledobódott burkot, ezzel megakadályozza
a gyors kihűlést. A táguló maradvány így hónapokon keresztül
intenzíven sugároz (fotoszferikus
fázis).
Fe
bomlási lánc miatti energiafelszabadulás belülről fűti a
ledobódott burkot, ezzel megakadályozza
a gyors kihűlést. A táguló maradvány így hónapokon keresztül
intenzíven sugároz (fotoszferikus
fázis).
Kb. 3-4 hónappal a robbanást követően a burok annyira szétterjed,
sűrűsége annyira lecsökken, hogy
elkezd átlátszóvá válni (nebuláris fázis). A kisugárzott
energia ekkor már teljesen a
![]() Co
bomlásából származik. A radioaktív bomlás törvényéből:
Co
bomlásából származik. A radioaktív bomlás törvényéből:
A fentebb leírt magkollapszussal létrejövő szupernóvák mellett más mechanizmusú csillagrobbanások is léteznek. Ezekről bővebben a 2.5.2. fejezetben lesz szó.
Szeged 2013-05-01