Lagrange-pontok, Roche-térfogat

A kettőscsillagok fizikai mennyiségei közti egyik legáltalánosabb összefüggés Kepler 3. törvénye:

$${{A^3} \over {P^2}} =  {G \over {4 \pi^2}} (m_1 + m_2),$$ (2.32)

ahol $m_{1,2}$ a komponensek tömegei, A a relatív pálya fél nagytengelye ( $A = A_1 + A_2$, ahol $A_{1,2}$ a komponensek abszolút pályájának sugara a tömegközépponti rendszerben), P a keringési periódus.

A tömegközépponti rendszerben a pálya menti keringésből származó impulzusmomentum:

$$J_{\rm orb} =  {{2 \pi} \over P} {{m_1 m_2} \over {m_1 + m_2}} A^2.$$ (2.33)

Ha a komponensek forgását is figyelembe vesszük, a forgási impulzusmomentum:

$$J_{\rm rot} =  (\alpha_1 m_1 R_1^2 + \alpha_2 m_2 R_2^2) \omega,$$ (2.34)

ahol $\alpha_{1,2}$ a két komponens tömegeloszlására jellemző konstans (fősorozati csillagokra $\alpha \sim$ 0,01 - 0,1), $\omega = 2 \pi /P$ a keringés körfrekvenciája, és feltételeztük, hogy a csillagok forgása és keringése kötött (ami szoros kettős rendszerben gyakran teljesül).

A teljes impulzusmomentum a pályamomentum és a forgási momentum összege, azaz

$$J = J_{\rm orb} + J_{\rm rot} =  {{2 \pi} \over P} \left ( {{m_1 m_2} \over {m_1 + m_2}} A^2 + (\alpha_1 m_1 R_1^2 + \alpha_2 m_2 R_2^2) \right ).$$ (2.35)

A kettőscsillag gravitációs terének egy P = (x,y,z) koordinátájú pontjában a gravitációs potenciál értéke

$$\phi =  -{{G m_1} \over r_1} - {{G m_2} \over r_2} - {\omega \over 2} r_o^2,$$ (2.36)

ahol $r_{1,2}$ a P pontnak a két komponens tömegközéppontjától mért távolsága, $r_o$ pedig a forgástengelyre merőlegesen mért távolsága. Ha együttforgó koordináta-rendszert választunk, amelyben az x-tengely mindig átmegy a két csillagon, az origót a tömegközéppontba helyezzük, a forgástengelynek a z-tengelyt jelöljük, és a távolságegységnek a két komponens távolságát választjuk (azaz A=1), akkor a 2.32 egyenlet felhasználásával adódik

$$\phi =  -{\omega \over {1+q}} \left ( {1 \over r_1} + {q \over r_2} \right ) - {\omega \over 2} (x^2 + y^2),$$ (2.37)

ahol bevezettük a $q = m_2 / m_1$ jelölést (tömegarány).

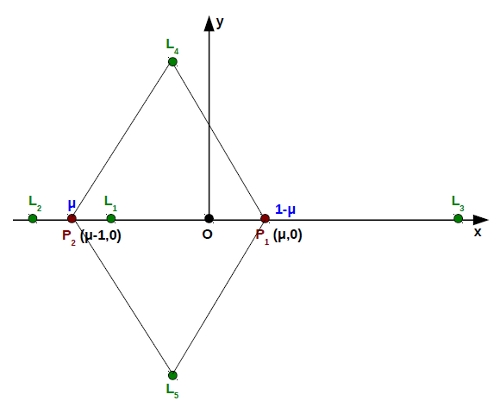
A 2.37 egyenlet által leírt potenciálfüggvénynek a két csillag közti szakaszon szélsőértéke, maximuma van. Ezen a helyen a potenciál hely szerinti első deriváltja zérus, azaz az ide helyezett próbatestre nem hat erő. Ez a hely a belső Lagrange-pont, amit $L_1$-gyel jelölnek. Hasonló pontok találhatók még az x-tengelyen a két komponensen túl ($L_2$ és $L_3$), valamint az x-y síkon a relatív pálya két ellentétes pontján ($L_4$ és $L_5$), ahogyan ezt a 2.6. ábra is szemlélteti.

2.6. Ábra: A Lagrange-pontok helyzete a $P_1$ és $P_2$ pontban lévő, $m_1$ és $m_2$ tömegpontok gravitációs terében. $\mu$ = $m_2$/($m_1$+$m_2$) az ún. redukált tömeg.

A belső Lagrange-ponton átmenő ekvipotenciális felületet nevezzük Roche-felületnek, az általa határolt térfogatot pedig Roche-térfogatnak. A két komponens Roche-térfogatának sugarát megadó közelítő képlet:

$$R_r(1) \approx  A ( 0.38 - 0.2 \log q )    R_r(2) \approx  A (0.38 + 0.2 \log q).$$ (2.38)