Next: Tömegátadás kompakt objektum esetén Up: Csillagfejlődés szoros kettős rendszerekben Previous: Lagrange-pontok, Roche-térfogat
Az ![]() pont
és a Roche-térfogat kiemelt jelentőségű a szoros kettőscsillagok
fejlődésében.
A komponensek egyensúlyi sugara dinamikai okokból nem lehet
nagyobb, mint a Roche-térfogat mérete.
A Roche-térfogatát kitöltő csillag anyaga az
pont
és a Roche-térfogat kiemelt jelentőségű a szoros kettőscsillagok
fejlődésében.
A komponensek egyensúlyi sugara dinamikai okokból nem lehet
nagyobb, mint a Roche-térfogat mérete.
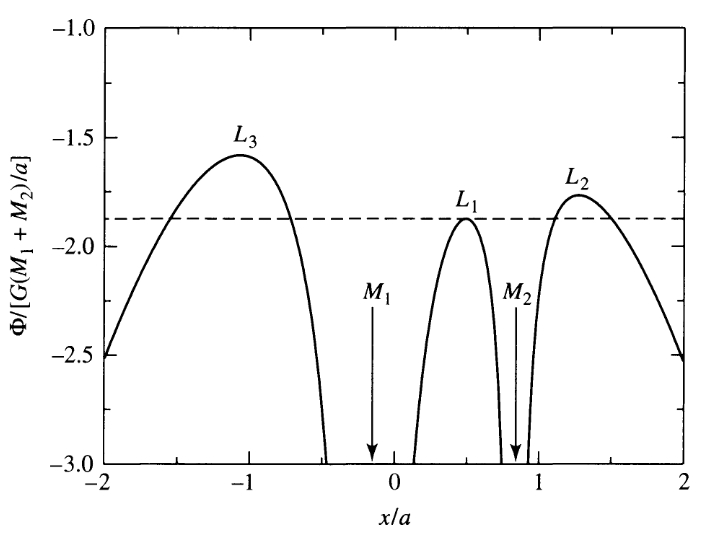
A Roche-térfogatát kitöltő csillag anyaga az ![]() ponton keresztül átáramolhat a
másik
komponensre (illetve a másik komponens által gravitációsan
``uralt'' térrészbe, lásd
2.7. ábra), így a rendszer
tömegaránya megváltozik. A változó tömegarány a pályákat is
megváltoztatja, így a szoros
kettőscsillagok
fejlődése jelentősen eltérhet a magányos csillagoknál
tapasztaltaktól.
ponton keresztül átáramolhat a
másik
komponensre (illetve a másik komponens által gravitációsan
``uralt'' térrészbe, lásd
2.7. ábra), így a rendszer
tömegaránya megváltozik. A változó tömegarány a pályákat is
megváltoztatja, így a szoros
kettőscsillagok
fejlődése jelentősen eltérhet a magányos csillagoknál
tapasztaltaktól.
 |
A Roche-térfogat kitöltése nemcsak a csillag méretétől, hanem a kettős rendszer egyéb paramétereitől is függ. Kepler 3. törvénye (2.32 egyenlet) ilyen alakba is írható:
A csillagok fejlődésük során különböző időszakokban képesek a méretüket jelentősen megnövelni. Mivel a nagyobb tömegű csillagok gyorsabban fejlődnek, a nagyobb tömegű főkomponens lesz az, amelyik először képes a Roche-térfogatát kitölteni. Az első (lassú) méretnövekedés még a fősorozati (magbeli hidrogénégető) szakaszban történik. Ha a főkomponens már ekkor kitölti a Roche-lebenyét, A típusú tömegátadásról beszélünk. Ha a fősorozati szakaszban nem, hanem az óriáságon, de még a magbéli He-égés beindulása előtt történik a kitöltés, akkor B típusú tömegátadás jön létre. Ha pedig a He-égés után, a szén-égés beindulása előtt történik meg a kitöltés, C típusú tömegátadás következik be.
A tömegcsere hatására megváltozik a komponensek tömegaránya, és a
keringés egyéb paraméterei is.
Konzervatív tömegátadásról akkor beszélünk, ha a tömegcsere
során a rendszer össztömege
(M) és teljes impulzusmomentuma (J) állandó marad
(most csak a pályamomentumot
tekintjük). A 2.32 és 2.33 egyenletek felhasználásával
megkaphatjuk, hogy ![]() tömeg
tömeg
![]() -ről
-ről ![]() -re történő
átáramlása esetén a relatív pálya fél nagytengelyének
megváltozása:
-re történő
átáramlása esetén a relatív pálya fél nagytengelyének
megváltozása:
A fenti képletekből látható, hogy ha ![]() , akkor
, akkor ![]() és
és ![]() , azaz
ha a tömeget adó
(donor-) csillag a nagyobb tömegű, mind a pálya mérete, mind a
periódus csökken, tehát a csillagok közelebb kerülnek egymáshoz és
a keringésük felgyorsul. Fordítva, ha a donorcsillag
kisebb tömegű, a nagytengely (szeparáció) növekszik és a keringés
lassul. Egyszerűen belátható,
hogy a minimális pályaméret és -periódus akkor következik be,
amikor a tömegek kiegyenlítődnek,
azaz
, azaz
ha a tömeget adó
(donor-) csillag a nagyobb tömegű, mind a pálya mérete, mind a
periódus csökken, tehát a csillagok közelebb kerülnek egymáshoz és
a keringésük felgyorsul. Fordítva, ha a donorcsillag
kisebb tömegű, a nagytengely (szeparáció) növekszik és a keringés
lassul. Egyszerűen belátható,
hogy a minimális pályaméret és -periódus akkor következik be,
amikor a tömegek kiegyenlítődnek,
azaz ![]() .
Ekkor
.
Ekkor
A fenti képletek szerint a tömegarány a tömegátadás sebességét
nagymértékben befolyásolja.
A csillagfejlődés során először a nagyobb tömegű főkomponens tölti
ki a Roche-lebenyét, tehát
az első tömegátadásnál ![]() . Mivel ekkor a nagytengely (A)
csökken, a Roche-lebeny
. Mivel ekkor a nagytengely (A)
csökken, a Roche-lebeny
![]() sugara is csökkenni fog (2.38.
egyenlet), ezért a Roche-térfogat kitöltöttsége
fokozódik. A pozitív visszacsatolás miatt a tömegátadás egyre
gyorsuló ütemben történik
meg, a számítások szerint a szabadesési időskálán (gyors
tömegátadás). Ez legalább addig
tart, amíg a tömegarány ki nem egyenlítődik, de a pontosabb
számítások szerint a tömegarány
akár meg is fordulhat. Ennek hatására a kezdetben nagyobb tömegű
csillag válik a kisebb
tömegű mellékkomponenssé.
sugara is csökkenni fog (2.38.
egyenlet), ezért a Roche-térfogat kitöltöttsége
fokozódik. A pozitív visszacsatolás miatt a tömegátadás egyre
gyorsuló ütemben történik
meg, a számítások szerint a szabadesési időskálán (gyors
tömegátadás). Ez legalább addig
tart, amíg a tömegarány ki nem egyenlítődik, de a pontosabb
számítások szerint a tömegarány
akár meg is fordulhat. Ennek hatására a kezdetben nagyobb tömegű
csillag válik a kisebb
tömegű mellékkomponenssé.
Ha ettől eltérő módon a kisebb tömegű csillag tölti ki a
Roche-lebenyét, tehát ![]() , akkor a 2.41 és 2.42 képletek értelmében a nagytengely és a
periódus nő,
tehát a csillagok távolodnak egymástól. Ennélfogva a
Roche-térfogat sugara is növekszik.
A Roche-lebeny kitöltöttsége tehát csökken, akár meg is szűnhet. A
csillagnak egyre növelnie
kell a sugarát, hogy a kitöltés és a tömegátadás továbbra is
fennmaradjon, ami egy lassú,
a nukleáris időskálán lejátszódó folyamat. Ez a szakasz a lassú
tömegátadás.
, akkor a 2.41 és 2.42 képletek értelmében a nagytengely és a
periódus nő,
tehát a csillagok távolodnak egymástól. Ennélfogva a
Roche-térfogat sugara is növekszik.
A Roche-lebeny kitöltöttsége tehát csökken, akár meg is szűnhet. A
csillagnak egyre növelnie
kell a sugarát, hogy a kitöltés és a tömegátadás továbbra is
fennmaradjon, ami egy lassú,
a nukleáris időskálán lejátszódó folyamat. Ez a szakasz a lassú
tömegátadás.
Szoros kettős rendszerek megfigyelése során kiderült, hogy számos esetben a fősorozatról már elfejlődött komponens kisebb tömegűnek bizonyult, mint a nagyobb tömegű, ámde még fősorozati állapotú csillag (Algol-paradoxon). Erre a látszólagos ellentmondásra a kettőscsillagokban lejátszódó, fentebb részletezett tömegátadási folyamatok felismerése adta meg a magyarázatot.
Szeged 2013-05-01