A csillagok anyaga nagyrészt teljesen ionizált plazma, amit ideális gáznak tekinthetünk.
Ideális gázban a részecskék szabadon mozognak,
és közöttük az ütközésen kívül más kölcsönhatás nem történik. Ekkor a
klasszikus statisztikus fizikában tanult gondolatmenet szerint a nyomás
a következő integrállal fejezhető ki:
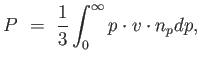 |
(1.10) |
ahol p a részecskék impulzusa, v a sebessége, 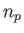 a p impulzusú részecskék
koncentrációja (azaz az ilyen részecskék száma egységnyi térfogatban). Ha ebbe az
összefüggésbe behelyettesítjük a T hőmérsékletű közegben p impulzusú részecskék
számát megadó Maxwell-Boltzmann-eloszlásfüggvényt, elemi integrálok kiszámítása után
adódik:
a p impulzusú részecskék
koncentrációja (azaz az ilyen részecskék száma egységnyi térfogatban). Ha ebbe az
összefüggésbe behelyettesítjük a T hőmérsékletű közegben p impulzusú részecskék
számát megadó Maxwell-Boltzmann-eloszlásfüggvényt, elemi integrálok kiszámítása után
adódik:
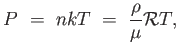 |
(1.11) |
ahol n a teljes részecskekoncentráció, k a Boltzmann-állandó, 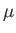 a közeg
átlagos molekulasúlya (1 részecskére eső átlagos tömeg atomi tömegegységekben),
a közeg
átlagos molekulasúlya (1 részecskére eső átlagos tömeg atomi tömegegységekben),
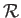 az egyetemes gázállandó. (1.11) nem más,
mint az ideális gáz jól ismert állapotegyenlete.
az egyetemes gázállandó. (1.11) nem más,
mint az ideális gáz jól ismert állapotegyenlete.
Szeged
2013-05-01