Next: Fedésidőpont-változás tranzitos exobolygóknál Up: Változócsillagok Previous: A fényidő-effektus
Irwin (1952, 1959) vizsgálta először részletesebben a fényidő-effektust, fedési kettős és harmadik test esetében.
Számoljuk ki egy ellipszis-pályán keringő csillag radiális
sebességét (Szatmáry 1987)! A pálya
geometriája a 3.100. ábrán látható (O
a tömegközéppont, z a látóirányú
elmozdulás, r a rádiuszvektor, v a valódi
anomália, ![]() a pericentrum-hosszúság,
i az inklináció, a a fél nagytengely,
a pericentrum-hosszúság,
i az inklináció, a a fél nagytengely, ![]() a keringési
periódus). Onnan leolvasható,
hogy
a keringési
periódus). Onnan leolvasható,
hogy
A radiális sebesség:
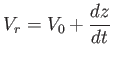 |
(3.60) |
Időben változó mennyiség r és v, így
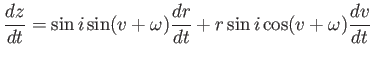 |
(3.61) |
Az égi mechanikából jól ismert, hogy
és
Ezek alapján
![$\displaystyle
V_r(v)=V_0+\frac{2\pi a\sin i}{P_o\sqrt{1-e^2}} \left
[ \cos (v+\omega) + e \cos \omega \right ]$](img666.png) |
(3.64) |
A radiális sebesség szélsőértékei:
| (3.65) |
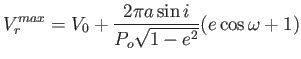 |
(3.66) |
| (3.67) |
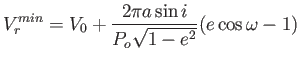 |
(3.68) |
Legyen
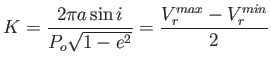 |
(3.69) |
a sebességamplitúdó, így a radiális sebesség
| (3.70) |
Az E excentrikus anomália függvényében ugyanez (Szatmáry 1987):
![$\displaystyle V_r(E)=V_0+K\left
[ \frac{(1-e^2)\cos \omega \cos E - \sqrt{1-e^2}\sin
\omega \sin E}{1-e \cos E} \right ]$](img673.png) |
(3.71) |
Nézzük meg ezután az O-C alakját a valódi anomália függvényében:
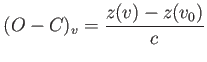 |
(3.72) |
(3.59), (3.62) és (3.63) alapján
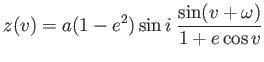 |
(3.73) |
így
![$\displaystyle (O-C)_v=\frac{a
\sin i}{c} (1-e^2) \left [ \frac{\sin (v+\omega)}{1+e
\cos v} \right ]_{v_0}^v$](img676.png) |
(3.74) |
Látható, hogy az O-C görbe alakját e és ![]() határozza meg.
határozza meg.
Az E excentrikus anomália függvényében ugyanez (Szatmáry 1987):
![$\displaystyle (O-C)_E=\frac{a
\sin i}{c} \left [ \sqrt{1-e^2} \cos \omega \sin E +
\sin \omega \cos E \right]_{E_0}^E$](img677.png) |
(3.75) |
A radiális sebesség és az O-C görbék kiszámításánál az excentrikus anomáliával felírt alakot használjuk, amikor megoldjuk a
| (3.76) |
Kepler-egyenletet, ahol
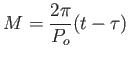 |
(3.77) |
a középanomália, ![]() pedig a pericentrumon való áthaladás időpontja. A
transzcendens Kepler-egyenletet az excentrikus anomália
Bessel-függvény együtthatójú trigonometrikus
sorfejtésével is megoldhatjuk. A 3.101.-3.104. ábrákon láthatóak a görbék
(
pedig a pericentrumon való áthaladás időpontja. A
transzcendens Kepler-egyenletet az excentrikus anomália
Bessel-függvény együtthatójú trigonometrikus
sorfejtésével is megoldhatjuk. A 3.101.-3.104. ábrákon láthatóak a görbék
(![]() =0,1
nap,
=0,1
nap, ![]() =1000
nap,
=1000
nap, ![]() =0 és
K=25 km/s bemenő adatok mellett).
=0 és
K=25 km/s bemenő adatok mellett).
Az O-C görbék alakja az excentricitás növekedésével egyre
aszimmetrikusabb, a szinuszostól való
eltérésük egyre jelentősebb (különösen kis ![]() értékeknél). Nagy
excentricitásnál
értékeknél). Nagy
excentricitásnál
![]() környékén a fázis nagy részében parabolához
hasonló az O-C alakja, így ezzel is
meg lehet próbálni az olyan O-C görbék illesztését, amelyeket
egyébként rendszerint parabolával
szoktak közelíteni. Így két egészen más magyarázat is szóba jöhet:
tág kettős rendszerben
másodkomponens léte vagy evolúciós periódusváltozás.
környékén a fázis nagy részében parabolához
hasonló az O-C alakja, így ezzel is
meg lehet próbálni az olyan O-C görbék illesztését, amelyeket
egyébként rendszerint parabolával
szoktak közelíteni. Így két egészen más magyarázat is szóba jöhet:
tág kettős rendszerben
másodkomponens léte vagy evolúciós periódusváltozás.
Az O-C görbék kevésbé változatosak és jellegzetesek, mint a
radiálissebesség-görbék,
így ránézésre azokból nehezebb e és ![]() értéket becsülni.
értéket becsülni.
Ahhoz, hogy egy pulzáló változó kettőssége megállapítható legyen az O-C diagramjából, legalább néhány keringési perióduson keresztül meg kell figyelni. Másik lényeges kívánalom, hogy a LITE hullám amplitúdója nagyobb legyen az O-C pontok hibájánál.
Szeged 2013-05-01