A fedési és pulzáló változócsillagok egyik legfontosabb paramétere a fényváltozás periódusa. Sok esetben a megfigyelhető fényességváltozás szigorúan periodikusan ismétlődik, más esetben pedig felépíthető különböző periódusú komponensek összegeként. Bármelyik esetet is tekintjük, általában éveken, évtizedeken átívelő megfigyelési sorozatok szükségesek a pontos periodicitások meghatározására. Különösen érdekesek azok az esetek, ahol a periódus megváltozik. Ilyenkor a változások jellege elárulhatja azok okát, például a csillagfejlődési hatásokat, vagy kettős rendszerben történő keringést.
Jelen dolgozatban olyan vizsgálatokat mutatok be, melyek 2000 és 2002 között elvégzett fényességméréseken alapulnak. Az általam tanulmányozott változócsillagok többsége egyszeresen periodikus fényváltozású, így méréseimmel az évtizedes időskálájú periódusváltozásokat tudtam megvizsgálni. Két esetben a rövidperiódusú pulzáló csillagok többszörös periodicitását találtam, amelyet a többmódusú pulzáció jeleként értelmeztem.
Diákköri dolgozatom felépítése a következő. Legelőször röviden áttekintem az
egyszeres és többszörös periodicitás jelentését a változócsillagok esetében.
Ismertetem a tanulmányozott két fő változócsillag-osztály, a fedési és pulzáló
változócsillagok legfontosabb tulajdonságait. Ezek után a bő másfél év során
használt műszereket ismertetem, kezdve a Szegedi Csillagvizsgáló távcsöveitől
egészen a Sierra Nevadai Obszervatórium műszeréig. Mivel munkámon végigvonul
az ![]() diagram alkalmazása, röviden tárgyalom a módszer néhány egyszerű tulajdonságát.
diagram alkalmazása, röviden tárgyalom a módszer néhány egyszerű tulajdonságát.
A dolgozatom gerincét az eredmények ismertetése teszi ki. Elsőként a fedési
kettőscsillagokkal kapcsolatos vizsgálataimat részletezem, melyekben a periódusvizsgálatok
mellett néhány egyszerű többszín-fotometriai meggondolás is megjelenik. Legtöbb
megfigyelést ![]() Scuti-típusú csillagokról végeztem, így munkám közel felét
az északi ég 11 magnitúdónál fényesebb nagyamplitúdójú
Scuti-típusú csillagokról végeztem, így munkám közel felét
az északi ég 11 magnitúdónál fényesebb nagyamplitúdójú ![]() Scuti-csillagainak
fotometriai felmérése és az első eredmények bemutatása teszi ki. Végezetül egy
többszörösen periodikus
Scuti-csillagainak
fotometriai felmérése és az első eredmények bemutatása teszi ki. Végezetül egy
többszörösen periodikus ![]() Scuti-csillag, a V784 Cassiopeiae frekvencia-analízisét
mutatom be.
Scuti-csillag, a V784 Cassiopeiae frekvencia-analízisét
mutatom be.
Diákköri munkámat rövid összefoglalással fejezem be. A 2000 augusztusa és 2002 januárja között elvégzett mérések segítségével alapos betekintést nyertem a rövidperiódusú változócsillagok közé, melynek részleteit az itt következő oldalakon olvashatjuk.
Dolgozatomban változócsillagok fényváltozását vizsgáltam saját, valamint irodalmi
mérési adatok alapján. Mivel vizsgálataim elsődleges célja a fénygörbék periodicitásának,
illetve annak finom változásainak kimutatása és értelmezése, ebben a pontban
röviden összefoglalnám, hogy milyen alapjelenségek felelnek a változások sokszor
alig
![]() -os relatív ingadozással mérhető periodicitásaiért. Először
az alapfogalmakat adom meg.
-os relatív ingadozással mérhető periodicitásaiért. Először
az alapfogalmakat adom meg.
Változócsillagok egyszeres periodicitása alatt azt értjük, ha a csillag bizonyos paramétere (például fényessége, radiális sebessége) egy bizonyos időintervallumban ismétlődően ugyanolyan mértékben változik, azaz szigorúan periodikus változást mutat. Az ilyen ismétlődő változások három fő ok miatt jöhetnek létre:
1. két csillag egymás körüli keringése;
2. a csillag pulzációja;
3. a csillag tengely körüli forgása.
Kettőscsillagok esetén a keringés során a csillagok radiális sebességének periodikus változása figyelhető meg. Ha mozgásuk pályájára úgy látunk rá, hogy elfedik egymást, akkor periodikus fényességcsökkenéseket is megfigyelhetünk.
Egy csillag pulzációja azt jelenti, hogy a csillag változtatja sugarát (radiális pulzáció) és/vagy felszínének szomszédos tartományai különböző fázisban mozognak (nemradiális pulzáció), gyakran igen szigorú periodicitást mutatva. Ez mind radiális sebesség, mind fényességméréssel kimutatható.
A csillagok tengely körüli forgása is okozhat periodikus változásokat. Ha egy csillag felszínén elég nagy folt található, akkor a tengelyforgás következtében ciklikus fényességváltozásokat figyelhetünk meg. Ezek a foltok több tucat rotációs periódus során fennmaradhatnak. Jól ismert forgási változócsillagok például a neutroncsillagok, melyekben a mágneses és a forgási tengely nem esik egybe. A mágneses tengely változó láthatóságának és a csillag hihetetlenül gyors tengelyforgásának következtében nagyon szabályos változások mutathatók ki széles hullámhossztartományban (rádiótól a röntgen hullámhosszakig). A változások nagyon rövid időskálán (másodperc vagy annak törtrésze alatt) játszódnak le. Ezeket az objektumokat nevezzük pulzároknak.
A többszörös periodicitás fogalma azt jelenti, hogy a csillagban megfigyelt változásokat több, hasonló vagy akár különböző okból eredő periodikus folyamat okozza. Pulzáló változócsillagoknál nagyon gyakori jelenség, hogy a fénygörbén a pulzáció amplitúdójában hosszabb-rövidebb periódusú modulációja figyelhető meg.
A többszörös periodicitású jelenségeket két nagyobb csoportra oszthatjuk, ha a kiváltó tényező alapján vizsgálódunk:
1. nem pulzációs eredetű;
2. pulzációs eredetű.
Az első csoportba olyan csillagtípusokat értünk, amelyek esetén a pulzációs eredetű fényváltozások mellett rotációból vagy kitörésekből származó változások is megfigyelhetőek. Ezenkívül számos fedési és spektroszkópiai kettőscsillagot ismerünk, ahol az egyik vagy olykor mindkét komponens pulzál (Szatmáry 1987).
A második csoportba olyan csillagokat sorolunk, amelyekben több frekvenciájú pulzáció (radiális és nem radiális módus) is egyidejűleg van jelen. Ez alapján tovább oszthatjuk ezt a csoportot a módusok gerjesztettsége szerint. Így három alcsoportot szokás megkülönböztetni:
a. csak radiális módusok,
b. radiális és nemradiális módusok,
c. csak nemradiális módusok
vannak gerjesztve.
A radiális módusok együttes gerjesztettsége például a cefeidákra jellemző. Leggyakrabban az alapmódus és az első felhang fordul elő, de azért akad példa az alapmódus és második felhang, valamint az első és második felhang együttes jelenlétére (Kiss 1999).
Radiális és nemradiális módosok együttes jelenlétét általában ![]() Scuti-
és
Scuti-
és ![]() Cephei-típusú változóknál mutatják ki.
Cephei-típusú változóknál mutatják ki.
Nemradiális módusok pulzáló fehér törpék, valamint a gyorsan oszcilláló Ap-típusú változók körében jellemző. Számos csillag esetén sikerült már kimutatni akár néhány perces oszcillációkat. Ezek alapján egyre inkább úgy tűnik, hogy valamennyi csillag rezeg a sajátfrekvenciáin, csak sok esetben a mai méréstechnikákkal ez nem detektálható.
A pulzáló változócsillagok sok típusánál találunk többszörös periodicitást. Ennek jelentősége, hogy az elméleti modellekkel való összehasonlítás (számított periódusok és periódusarányok) révén meghatározhatók a vizsgált csillagok legfontosabb asztrofizikai paraméterei (ez az asztroszeizmológia feladata).
Ebben a fejezetben rövid áttekintést igyekszem adni az általam vizsgált két
fő változócsillag-típusról a fedési kettősökről, valamint a pulzáló ![]() Scuti-típusú csillagokról.
Scuti-típusú csillagokról.
A kettőscsillagok számos típusa közül most a fedési kettősöket jellemzem. A fedési kettősök olyan tömegközéppontjuk körül keringő csillagok, amelyeknél majdnem pontosan a keringési síkban látunk rá a pályára. Ennek következtében a komponensek elfedik egymást, ezért a kettősség egyértelműen kimutatható a fénygörbéből. Ebben az esetben a fénygörbe alakja elsősorban a csillagok szeparációjától és pályájuk inklinációjától függ.
A fénygörbék alakja szerint három alosztályba sorolhatók a fedési kettőscsillagok:
1. Algol-típus, amelyekre jellemző, hogy a két gömb alakú (vagy csak kevésbé eltorzult) komponens közti távolság jóval meghaladja a két csillag sugarát. Ennek következtében fedésen kívül állandó, míg fedéskor hirtelen csökkenő fényességet tapasztalhatunk. A főminimumban akár több magnitúdós is lehet a fényességcsökkenés, a mellékminimum viszont nem igen haladja meg a tizedmagnitúdót sem. Előfordul olyan eset is ennél a típusnál, hogy annyira különböző felületi fényességűek a komponensek, hogy a mellékminimum alig különböztethető meg a fénygörbe állandó fényességű szakaszától.
A fő- és mellékminimum időbeli viszonyát erősen befolyásolhatja a pálya excentricitása.
Körpálya (e=0) esetén a mellékminimum két főminimum között félúton helyezkedik
el. Nagy excentricitás (0![]() e<1) esetén ettől eléggé eltérő helyen figyelhető
meg a mellékminimum.
e<1) esetén ettől eléggé eltérő helyen figyelhető
meg a mellékminimum.
A legkülönbözőbb keringési periódusok fordulnak elő 0,2 naptól akár 10000 napig.
2. A ![]() Lyrae-típusú fedési kettősök komponensei ellipszoidális
alakúak. Az összfényesség folyamatosan változik, a fedés kezdete és vége nem
határozható meg pontosan. Ezeknél a csillagoknál mindig látszik a mellékminimum
is, ami mindig kisebb mélységű a főminimumnál.
Lyrae-típusú fedési kettősök komponensei ellipszoidális
alakúak. Az összfényesség folyamatosan változik, a fedés kezdete és vége nem
határozható meg pontosan. Ezeknél a csillagoknál mindig látszik a mellékminimum
is, ami mindig kisebb mélységű a főminimumnál.
A fényváltozási amplitúdó általában kisebb 2![]() 0-nál, periódusuk pedig hosszabb
egy napnál.
0-nál, periódusuk pedig hosszabb
egy napnál.
3. A W UMa-típusú fedési kettőscsillagok két egymáshoz nagyon hasonló, ellipszoidális komponensből állnak. Periódusuk rövidebb egy napnál, leginkább a 0,2 és 0,4 nap közötti érték jellemző. A fénygörbéjükön a fő- és mellékminimum közel egyforma mély és folyamatosan változik a fényesség.
Dolgozatomban a fedési kettősök három típusához tartozó csillagok közül kettővel
foglalkoztam: egy Algol-típusúval, amely hosszú periódusú (P![]() 1277 nap),
és eléggé excentrikus (e=0,55) pályán mozog, valamint két, közel nyolc órás
periódussal keringő W UMa-típusú változóval.
1277 nap),
és eléggé excentrikus (e=0,55) pályán mozog, valamint két, közel nyolc órás
periódussal keringő W UMa-típusú változóval.
A pulzáló változócsillagoknál a fényesség időbeli változását a csillag méretének
és hőmérsékletének változása okozza. Ezen belül számos altípust különböztetünk
meg. Ebben a fejezetben az egyik leggyakrabban előforduló pulzáló csillagfajtát,
a ![]() Scuti-csillagok fő jellemzőit mutatom be, mivel megfigyeléseim nagy
részét ez a típus képezi.
Scuti-csillagok fő jellemzőit mutatom be, mivel megfigyeléseim nagy
részét ez a típus képezi.
A ![]() Scuti-típusú változók a Hertzsprung-Russell-diagram ún. instabilitási
sávjában helyezkednek el, közel a fősorozathoz. Fiatal, közepes tömegű (1
Scuti-típusú változók a Hertzsprung-Russell-diagram ún. instabilitási
sávjában helyezkednek el, közel a fősorozathoz. Fiatal, közepes tömegű (1![]() 2
M
2
M![]() ), A
), A![]() F (T
F (T![]() =7000
=7000 ![]() 9000 K) színképtípusú törpe, esetleg
szubóriás (általában
9000 K) színképtípusú törpe, esetleg
szubóriás (általában ![]() 1
1![]() 2 R
2 R![]() ) csillagok. Néhány órás periódussal
és néhány század-, egy-két tizedmagnitúdós amplitúdóval pulzálnak. Gyakran fordul
elő, hogy fénygörbéjük többszörös periodicitású, amelynek oka, hogy egyszerre
több módus gerjesztett. Radiális és nemradiális módusok egyaránt kimutathatóak,
amelyek egyértelműen csak nagyfelbontású spektroszkópia segítségével különböztethetőek
meg. Elméleti modellek alapján a frekvenciaarányokból is azonosítják az egyes
módusok fajtáit.
) csillagok. Néhány órás periódussal
és néhány század-, egy-két tizedmagnitúdós amplitúdóval pulzálnak. Gyakran fordul
elő, hogy fénygörbéjük többszörös periodicitású, amelynek oka, hogy egyszerre
több módus gerjesztett. Radiális és nemradiális módusok egyaránt kimutathatóak,
amelyek egyértelműen csak nagyfelbontású spektroszkópia segítségével különböztethetőek
meg. Elméleti modellek alapján a frekvenciaarányokból is azonosítják az egyes
módusok fajtáit.
Mivel dolgozatom nagy részét a ![]() Scuti-csillagok egy csoportja teszi
ki, ezért megemlítem még, hogy szokás a
Scuti-csillagok egy csoportja teszi
ki, ezért megemlítem még, hogy szokás a ![]() Scuti-csillagokon belül egy
családot megkülönböztetni, amelyeket nagyamplitúdójú
Scuti-csillagokon belül egy
családot megkülönböztetni, amelyeket nagyamplitúdójú ![]() Scuti-változóknak
hívnak. Ebbe a családba jórészt monoperiodikus változók tartoznak, periódusuk
jellemzően 0,1 nap körüli, amplitúdójuk pedig 0
Scuti-változóknak
hívnak. Ebbe a családba jórészt monoperiodikus változók tartoznak, periódusuk
jellemzően 0,1 nap körüli, amplitúdójuk pedig 0![]() 4
4![]() 0
0![]() 6 közé esik. A nagyamplitúdójú
6 közé esik. A nagyamplitúdójú
![]() Scuti-csillagoknak létezik II. populációs megfelelője, amelyeket SX
Phoenicis-típusú változóknak neveznek.
Scuti-csillagoknak létezik II. populációs megfelelője, amelyeket SX
Phoenicis-típusú változóknak neveznek.
Ebben az alfejezetben azokat a műszereket mutatom be, amelyekkel méréseimet végeztem. A távcsöveket átmérőjük szerint növekvő sorrendben ismertetem. A címekben szereplő rövidítések az alkalmazott műszereket kódolják: később röviden ezekkel hivatkozok rájuk.
A távcső a Szegedi Tudományegyetem Béke épületének tetején található. Egy 28
cm-es belépő nyílású f/6,3 Schmidt-Cassegrain-típusú távcső. A műszert a Celestron
cég gyártotta, mechanikája ekvatoriális szerelésű. A mérésemkor a képek felvételére
egy SBIG ST![]() 9E típusú CCD kamerát használtam. Ennek fő jellemzői: 512
9E típusú CCD kamerát használtam. Ennek fő jellemzői: 512![]() 512
pixel, 20
512
pixel, 20![]() 20
20 ![]() -os pixelméret, 16 bites AD konverter.
-os pixelméret, 16 bites AD konverter.

A Szegedi Csillagvizsgáló mérőműszere, amely a város szélén található. A távcső
f/14-es fényerejű, 40 cm-es átmérőjű és Cassegrain-típusú1(l. Fűrész 2000). A mechanika ekvatoriális szerelésű. A detektor ugyanaz az
SBIG ST![]() 9E típusú CCD kamera, amelyet a 28 cm-es távcsőnél használtam. A méréseket
a Johnson-féle fotometriai rendszer szűrőivel végeztem.
9E típusú CCD kamera, amelyet a 28 cm-es távcsőnél használtam. A méréseket
a Johnson-féle fotometriai rendszer szűrőivel végeztem.

A Johnson-féle rendszer
A legelterjedtebb fotometriai rendszert kezdetben UBV szűrőket definiálták.
Később kiterjesztették az infravörös tartományra is a rendszert az R, I, J,
K, L, M és N szűrőkkel. A rendszer szélessávú (
![]() )
szűrőket tartalmaz, melyek közül a BVRI szűrőket használtam. Főbb adataikat
az 1. táblázat tartalmazza.
)
szűrőket tartalmaz, melyek közül a BVRI szűrőket használtam. Főbb adataikat
az 1. táblázat tartalmazza.
| szűrő | központi hullámhossz (nm) | sávszélesség (nm) |
| B | 440 | 100 |
| V | 550 | 90 |
| R | 700 | 200 |
| I | 850 | 230 |
A közvetlenül mért, úgynevezett instrumentális magnitúdókat a standard fotometriai
rendszerbe lineáris transzformációkkal visszük át, melyek differenciális esetben
a következő alakúak (Henden és Kaitchuk 1982):
Saját méréseket végeztem annak érdekében, hogy a szegedi 40 cm-es távcső transzformációs együtthatóit meghatározzam. Ehhez az M67 nyílthalmaz fotometriai standard csillagait használtam fel (Chevalier és Ilovaisky 1991). Ennek alapján a 2. táblázatban szereplő transzformációs együtthatókat határoztam meg a távcsőre.
Jól látszik, hogy az ideális esethez képest (
![]() )
a szegedi szűrők által definiált rendszer kicsit eltér a standardtól. Mindazonáltal
a távcsőkonstansokat megadó összefüggések a vizsgált színtartományban nagy pontossággal
lineárisak, így a standard transzformációk megbízhatóan alkalmazhatók.
)
a szegedi szűrők által definiált rendszer kicsit eltér a standardtól. Mindazonáltal
a távcsőkonstansokat megadó összefüggések a vizsgált színtartományban nagy pontossággal
lineárisak, így a standard transzformációk megbízhatóan alkalmazhatók.
| együttható jele | együttható értéke |
| 1,131 |
|
| 0,113 |
|
| 1,230 |
|
| 0,215 |
|
| 1,063 |
Méréseim egy részét az MTA Csillagászati Kutatóintézet Piszkéstetői Obszervatóriumának
f/3-as, Schmidt-típusú távcsövével végeztem. A távcső belépő nyílása 60 cm,
a tükör átmérője 90 cm, mechanikája villás parallaktikus. A detektor Photometrics
AT![]() 200 CCD kamera. Paraméterei:
200 CCD kamera. Paraméterei:
![]() pixel, pixelmérete 9
pixel, pixelmérete 9 ![]() ,
14 bites, AD konverter. Az elért látómező
,
14 bites, AD konverter. Az elért látómező
![]() .
.
A Piszkéstetői Obszervatórium műszerére is meghatároztam a transzformációs együtthatókat, amelyeket a következő táblázatban foglalok össze:
| együttható jele | együttható értéke |
| 0,925 |
|
| 0,098 |
|
| 1,037 |
|
| 0,219 |
|
| 1,011 |
A spanyolországi Insituto de Astrofísica de Andalucía Sierra Nevadai Obszervatóriumának
90 cm-es távcsövét 2001 nyarán két héten keresztül használtam méréseimhez. Az
obszervatórium tengerszint feletti magassága 2896 m. A műszer 90 cm-es átmérőjű
f/8-as Ritchey-Chrétien-típusú. A detektor egy négycsatornás spektrofotométer,
amely a Strömgren-féle fotometriai rendszert valósítja meg. A mérésekhez 28
![]() -os
apertúrát használtam.
-os
apertúrát használtam.

A Strömgren-rendszer
A Strömgren-rendszer közepes sávszélességű szűrőket használ, ezek az u - ultraibolya, v - ibolya, b - kék, y - sárga. Az effektív hullámhosszakat a 4. táblázatban mutatom be.
| szűrő | központi hullámhossz (nm) | sávszéleség (nm) |
| u | 350 | 34 |
| v | 410 | 20 |
| b | 470 | 16 |
| y | 550 | 24 |
Ennek a rendszernek számos előnye van a Johnson-féle rendszerrel szemben. Ezek
közül most csak azt emelném ki, hogy a ![]() színindex megbízhatóbb hőmérséklet
indikátor a
színindex megbízhatóbb hőmérséklet
indikátor a ![]() színindexnél.
színindexnél.
Mivel a Strömgren-rendszer színindexei kevert indexek, azaz színindexek különbségei,
így a standard transzformáció más alakot ölt. Ezen kívül az y szűrőt úgy választották
meg, hogy központi hullámhossza megegyezzen a Johnson V szűrőével, ezért tulajdonképp
standard ``y'' fényesség nincs is, a transzformációs egyenletek Johnson-féle
V-t adnak. Tehát a standard transzformációs egyenletek differenciális fotometria
esetén így alakulnak (Kiss 1999):
Mivel a v szűrő lefedi a hőmérséklettel erősen változó H![]() vonalat, ezért
a vonal abszorpciós hatását a standard transzformációk extra
vonalat, ezért
a vonal abszorpciós hatását a standard transzformációk extra ![]() -tól függő
tagjaival vehetjük figyelembe. Az A, B, C, D, E, és F transzformációs együtthatók
ismert fényességű csillagok segítségével mérhetők ki. A Sierra Nevada Obszervatórium
esetén ezek az együtthatók a következők (Rodríguez, személyes közlés):
-tól függő
tagjaival vehetjük figyelembe. Az A, B, C, D, E, és F transzformációs együtthatók
ismert fényességű csillagok segítségével mérhetők ki. A Sierra Nevada Obszervatórium
esetén ezek az együtthatók a következők (Rodríguez, személyes közlés):
| együttható | A | B | C | D | E | F |
| értéke | 0,021 | 0,975 | 0,730 | 0,049 | 1,058 | 0,201 |
Ebben a pontban röviden ismertetem, hogyan történt a CCD képek feldolgozása, azaz milyen módon jutothattam el a képek felvételétől a kész fénygörbékig.
A CCD képekből az apertúra fotometria segítségével kaptam olyan adatokat, amelyekből el lehetett készíteni a fénygörbéket. Az apertúra fotometriát az IRAF noao/ digiphot/ apphot csomagjával végeztem. Itt csak azokat a paramétereket írom le, amelyeket minden egyes éjszaka képkiméréseinél változtatni kell.
Mielőtt a képeket kimértem, elvégeztem a képek flatkorrekcióját. Ez egy nagyon fontos korrekció, mert ennek segítségével tudjuk figyelembe venni az CCD egyes pixeleinek különböző mértékű érzékenységét, amely erősen befolyásolhatja a mérési eredményeket. Ennek elvégzésére a flatképek normált átlagát az imsum task-kal lehet elkészíteni, amelyben a flatképek listáját kell megadnunk bemenő paraméterként, kimenőként pedig azt a nevet, amelyet adni szeretnénk flatképünknek. Maga a flatkorrekció (amely során pixelenként osztjuk el az egyes képeket a flatképpel) a noao/ imred/ ccdred csomag ccdproc taskjával történik. Ebben a taskban csak a képek listáját és azt a flatképet kell megadnunk, amellyel korrigálni akarunk.
A képek kiméréséhez először is a daofind taskot használtam. Ennek a tasknak az a feladata, hogy egy CCD képen csillagokat keressen, és az egyes képeken megtalált csillagok adatait egy coo.1 kiterjesztésű file-ban tárolja. Ahhoz, hogy elvégezhesse feladatát, bizonyos paramétereket meg kell adnunk, amelyek a jellemzik az adott éjszaka képeit. Egy taskot az epar paranccsal lehet módosítani. A következő paramétereket kell meghatározni és értékeiket beírni a task paraméterlistájába:
-image: A képek listája.
-output: Itt a kimenetet lehet megadni. Ha default-ban hagyjuk, akkor coo.1 kiterjesztésű file-ok lesznek a kimenetben.
-datapars: Tulajdonképp ebben adjuk meg a képekre jellemző paramétereket. A következőket kell módosítani. Az fwhmpsf paraméterben a csillagok félértékszélességét, a sigma paraméterben a képek hátterének szórását kell megadni. Ezekhez a datapars-ból a :e billentyűkombinációval juthatunk.
-findpars: Ebben adhatjuk meg, hogy a háttérből hányszoros szórással kiemelkedő intenzitásértéket fogadja el csillagként.
Ezeket a paramétereket az imexam task-kal lehet meghatározni, amely ebből a
csomagból is elindítható. Ezt futtatva, és az r billentyű leütésével egy csillag
intenzitás-eloszlásáról radiális ábrát kaphatunk a pixelek (adott pixeltől való
távolság) függvényében. Ennek során kiírja a képernyőre a félértékszélességet,
amelyet a datapars taskban hasznosítunk. Erről a radiális ábráról lehet leolvasni
egy későbbi paramétert, hogy mekkora apertúrát kell majd használnunk magához
a fotometriához. Ezen kívül most még fontos számunkra a kiméréshez az m billentyű
lenyomására futó program, amely statisztikát ír ki a képernyőre egy 5![]() 5-ös
négyzetről. Ezzel kapunk felvilágosítást a háttér szórásáról.
5-ös
négyzetről. Ezzel kapunk felvilágosítást a háttér szórásáról.
A daofind task a :g paranccsal futtatható. Ennek lefutásával már egy kicsit felgyorsulnak az események. Megvannak az egyes képeken talált csillagok listája. A következő lépés ezen csillagok instrumentális magnitúdóinak meghatározása. Ez a phot task-kal történik. Ebben a következő paramétereket kell megadni:
-photpar: Az az apertúraméret, amellyel történik a fotometria. Amikor meghatározzuk ezt a paramétert, nagyon figyelmesnek kell lenni, mivel túl kis méretű apertúrát megadva a kimaradt részek intenzitása kiesik, ha pedig túl nagy az apertúra, akkor zajnövelő módon a hátteret is belevesszük a fotometriába.
-fitskypar: Ebben az apertúra minden egyes méretét megadhatjuk, azaz a gyűrű belső sugarát, vastagságát. A saját kiméréseimhez 3 pixel vastagságú apertúrát használtam.
Ezek után futtathatjuk a fotometriát. A futás végén mag.1 kiterjesztésű file-okban találhatóak a kapott fényességek.
A két task lefutásával létrejövő file-ok számos adatot tartalmaznak a képekről. Számomra a fénygörbék elkészítéséhez csak a fényességértékekre volt szükség, olykor pedig a csillagok koordinátáira. A keresett adatokat a txdump task-kal lehet kiszedni a file-okból. Ebben a taskban csak a bemenő (textfile) paramétert kell megadni, azaz azoknak a file-oknak a listáját, amelyek tartalmazzák a számunkra lényeges adatokat. Ezenkívül azokat a paraméterneveket kell beírni, amelyeket ki szeretnénk szedni a file-okból. Ezt a fields paraméterben tehetjük meg. Ebben és a képek neveivel (image) együtt a fényeségeket (mag), valamint ha szükséges volt a csillagok koordinátáit (xcenter, ycenter) írattam ki. Ennek a task-nak a futási eredményét célszerű nem a képernyőre, hanem egy file-ba átirányítani.
Ahhoz, hogy megkapjam a fénygörbéket, szükséges volt még az egyes fényességpontokhoz tartozó időpontok meghatározása. Ezt a noao/ imred/ kpnocoude csomag setjd task-jának segítségével lehet elvégezni. Ez a task a képek fejlécében található időpontokból és koordinátákból meghatározza a Julián-dátumot és a heliocentrikus Julián-dátumot. Ebben is csak a képek listáját kell megadni, majd a futtatást egy file-ba szoktam vezetni.
A fénygörbékhez szükséges adatokat egy Pascal program futtatásával nyertem ki. Ennek a programnak egyszerű a működése. Két file-ból (egyik az egyes képek neveit és az azokhoz tartozó időpontokat tartalmazza, másik pedig a képek neveit és a rajtuk talált csillagok magnitúdói fényesség szerint rendezve) képzi a megfelelő képek időpontját és ahhoz a megfelelő differenciális magnitúdóértékeket. Azért lehet ilyen egyszerűen megalkotni a fénygörbét, mert a megfigyeléseim során elkészített CCD képeken a változócsillag egy esetet kivéve mindig a legfényesebb csillag a látómezőben, összehasonlítókként pedig rendre a látómező második, illetve harmadik legfényesebb csillagait választottam. Az egyetlen kivételes eset a V567 Ophiuchi volt, ahol maximumban a legfényesebb, minimumban a második legfényesebb csillag volt a látómezőben. Ebben az esetben a koordináták figyelembevételével készítettem el az adatokat.
Az ![]() diagram elkészítéséhez szükség van a fénygörbék maximumának vagy minimumának
meghatározására. Ezt is egy Pascal program segítségével határoztam meg, amely
a fénygörbék maximumának illetve minimumának környezetére alacsony fokszámú
(általában ötödfokú) polinomot illeszt és ennek szélsőértékét határozza meg.
diagram elkészítéséhez szükség van a fénygörbék maximumának vagy minimumának
meghatározására. Ezt is egy Pascal program segítségével határoztam meg, amely
a fénygörbék maximumának illetve minimumának környezetére alacsony fokszámú
(általában ötödfokú) polinomot illeszt és ennek szélsőértékét határozza meg.
Az egyszeresen periodikus csillagok vizsgálatában a nagy múltra visszatekintő,
hagyományos ![]() módszert alkalmaztam. Mivel ez a módszer a periodikus folyamatok
tárgyalása esetén széles körben alkalmazható és magam is szinte minden esetben
ezt használtam, fontosnak éreztem, hogy részletesebben tárgyaljam a módszer
alapjait és néhány legfontosabb tulajdonságát.
módszert alkalmaztam. Mivel ez a módszer a periodikus folyamatok
tárgyalása esetén széles körben alkalmazható és magam is szinte minden esetben
ezt használtam, fontosnak éreztem, hogy részletesebben tárgyaljam a módszer
alapjait és néhány legfontosabb tulajdonságát.
Az ![]() diagram a szigorúan periodikusan lejátszódó folyamatok vizsgálatának
egyik eszköze, amellyel nagyon pontos (
diagram a szigorúan periodikusan lejátszódó folyamatok vizsgálatának
egyik eszköze, amellyel nagyon pontos (
![]() relatív pontosságú)
periódusmeghatározás lehetséges, illetve segítségével vizsgálhatók a periódus
finom változásai.
relatív pontosságú)
periódusmeghatározás lehetséges, illetve segítségével vizsgálhatók a periódus
finom változásai.
Alapfeltevése a következő:
Legyen ismert egy a vizsgált csillagászati jelenségre jellemző időpont (epocha,
![]() : pl. a maximális vagy minimális fényesség időpontja), valamint az ekkor
érvényes periódus értéke (
: pl. a maximális vagy minimális fényesség időpontja), valamint az ekkor
érvényes periódus értéke (
![]() : két egymást követő maximum vagy
minimum közt eltelt idő). A mérésekből meg lehet határozni a fényességmaximum,
illetve fényességminimum bekövetkezésének pillanatát. Így rendelkezésünkre áll
egy megfigyelt időpont (O=obszervált). Ezt össze lehet hasonlítani az adott
fénygörbejelenség bekövetkezésének számított (C=calculated) időpontjával.
Ezt az epocha és a számítások szerint azóta eltelt idő összegeként kapjuk. Ez
utóbbit úgy tudjuk megkapni, hogy a periódusra elfogadott értéket beszorozzuk
az adott epochától lezajlott ciklusok számával. Így a következő módon definiálhatjuk
egy tetszőleges megfigyelt maximum- vagy minimumidőpontban (
: két egymást követő maximum vagy
minimum közt eltelt idő). A mérésekből meg lehet határozni a fényességmaximum,
illetve fényességminimum bekövetkezésének pillanatát. Így rendelkezésünkre áll
egy megfigyelt időpont (O=obszervált). Ezt össze lehet hasonlítani az adott
fénygörbejelenség bekövetkezésének számított (C=calculated) időpontjával.
Ezt az epocha és a számítások szerint azóta eltelt idő összegeként kapjuk. Ez
utóbbit úgy tudjuk megkapni, hogy a periódusra elfogadott értéket beszorozzuk
az adott epochától lezajlott ciklusok számával. Így a következő módon definiálhatjuk
egy tetszőleges megfigyelt maximum- vagy minimumidőpontban (![]() ) az
) az ![]() értékét:
értékét:
A megfigyelt (O) és a számított (C) időpont közötti különbséget az idő vagy
a ciklusszám függvényében ábrázolva kapjuk az ![]() diagramot.
diagramot.
Az ![]() diagram vizsgálatában néhány egyszerű esetet különböztetünk meg. Legyen
diagram vizsgálatában néhány egyszerű esetet különböztetünk meg. Legyen
![]() a fényességváltozás valódi periódusa,
a fényességváltozás valódi periódusa, ![]() pedig az
pedig az ![]() diagram számításához
használt periódus.
diagram számításához
használt periódus.
1. ![]() ,
, ![]() ismert,
ismert, ![]() állandók
állandók
Ekkor az ![]() egyenes. Az időpont meghatározás pontatlanságai miatt
az
egyenes. Az időpont meghatározás pontatlanságai miatt
az ![]() pontok az egyenes körül szórnak.
pontok az egyenes körül szórnak.
2. ![]() ,
, ![]() ismert,
ismert, ![]() állandók
állandók
Ekkor ![]() :
:
Két esetet lehet megkülönböztetni:
a.) Ha a ![]() , akkor az
, akkor az
![]() kisebb lesz,
mint amit az
kisebb lesz,
mint amit az
![]() -vel számolnánk. Így egy negatív meredekségű
egyenest kapunk.
-vel számolnánk. Így egy negatív meredekségű
egyenest kapunk.
b.) Ha a ![]() , akkor az
, akkor az
![]() nagyobb értékeket
vesz fel, mint amit az
nagyobb értékeket
vesz fel, mint amit az
![]() -vel számolnánk. Így egy pozitív
meredekségű egyenest kapunk.
-vel számolnánk. Így egy pozitív
meredekségű egyenest kapunk.
Az ![]() kvázifolytonos függvényként is értelmezhető. Legyen
kvázifolytonos függvényként is értelmezhető. Legyen
![]() !
!
3. Vizsgáljuk meg azt az esetet, ha a periódus egyenletesen változik!
Legyen ez most az egyenletes periódusnövekedés esete! Változzon a periódus (![]() )
ciklusonként
)
ciklusonként
![]() -vel! Ekkor az n-edik megfigyelt időpont
a következőképp adódik:
-vel! Ekkor az n-edik megfigyelt időpont
a következőképp adódik:
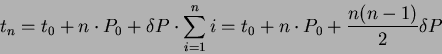
Számítsuk ki az ![]() diagramot valamilyen
diagramot valamilyen ![]() és
és ![]() efemerissel!
Ekkor a számított időpont:
efemerissel!
Ekkor a számított időpont:
Tegyük fel, hogy ![]() ,
,
![]() és
és
![]() !
Így a definíció alapján:
!
Így a definíció alapján:
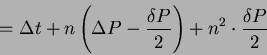
Tehát az egyenletes periódusváltozás esetén az ![]() diagram másodfokú függvény
lesz. Az
diagram másodfokú függvény
lesz. Az ![]() pontokra parabolát illesztve számíthatóak lesznek a korrekcióhoz
szükséges paraméterek:
pontokra parabolát illesztve számíthatóak lesznek a korrekcióhoz
szükséges paraméterek:
![]() : epocha-korrekció
: epocha-korrekció
![]() : periódus-korrekció
: periódus-korrekció
![]() : periódusváltozási ráta, amelyet
: periódusváltozási ráta, amelyet ![]() -val is szoktak jelölni
-val is szoktak jelölni
Megjegyzés: A ![]() az elsőfokú tagban is szerepel, de ez elhanyagolhatóan
kicsi általában a
az elsőfokú tagban is szerepel, de ez elhanyagolhatóan
kicsi általában a ![]() -hez képest.
-hez képest.
Az ![]() -re kapott formulából kitűnik, hogy csak diszkrét időpontokban van értelmezve.
Ennek ellenére az
-re kapott formulából kitűnik, hogy csak diszkrét időpontokban van értelmezve.
Ennek ellenére az ![]() diagramot kvázifolytonosnak tekinthetjük, ha elegendően
sok cikluson keresztül, azaz nagy időintervallumban vizsgáljuk a periódusváltozást.
diagramot kvázifolytonosnak tekinthetjük, ha elegendően
sok cikluson keresztül, azaz nagy időintervallumban vizsgáljuk a periódusváltozást.
Fény-idő effektus
Ha egy pulzáló változócsillag egy kettős rendszer tagja, akkor pályájának különböző
szakaszain látszólag más-más pulzációs periódus észlelhető. A tömegközéppont
körüli keringés miatt a periódus hossza periodikus változást mutat. Ez az ![]() diagram alakjából kimutatható. A keringés során a vizsgált csillag távolsága
változik a megfigyelőhöz képest, így a csillagról kisugárzott fénynek változó
nagyságú utat kell megtennie a pálya egyes szakaszain, azaz a kisugárzott jel
frekvenciája periodikus modulációt szenved. Ezt a jelenséget hívjuk fény-idő
effektusnak. A változócsillag
diagram alakjából kimutatható. A keringés során a vizsgált csillag távolsága
változik a megfigyelőhöz képest, így a csillagról kisugárzott fénynek változó
nagyságú utat kell megtennie a pálya egyes szakaszain, azaz a kisugárzott jel
frekvenciája periodikus modulációt szenved. Ezt a jelenséget hívjuk fény-idő
effektusnak. A változócsillag ![]() diagramja ekkor a látóirányra merőleges
síktól vett, időben változó távolságától függ, feltéve, hogy a csillagnak nincs
saját periódusváltozása.
diagramja ekkor a látóirányra merőleges
síktól vett, időben változó távolságától függ, feltéve, hogy a csillagnak nincs
saját periódusváltozása.
Legyen a periodikus jelforrás egy kettős rendszerben és mozogjon ![]() orbitális
periódussal! Ebben az esetben egy
orbitális
periódussal! Ebben az esetben egy ![]() időpontban
időpontban
![\begin{displaymath}O-C=\frac {a \cdot sin\ i}{c} \left( 1-e^{2} \right) \left[ \...
...sin \left( v_{0}+ \omega \right)}{1+e \cdot cos v_{0}} \right],\end{displaymath}](img85.png)
Figyelembe véve, hogy a valódi anomália időfüggéséhez az excentrikus anomálián
és a Kepler-egyenlet numerikus megoldásán keresztül jutunk el (Marik 1989),
adódik a következtetés, hogy az ![]() diagram időfüggésére nincs zárt, analitikus
formula. Gyakorlatban a megfigyelt
diagram időfüggésére nincs zárt, analitikus
formula. Gyakorlatban a megfigyelt ![]() diagramokat illesztjük a fenti elméleti
alakkal, amelyből három pályaelem adódik.
diagramokat illesztjük a fenti elméleti
alakkal, amelyből három pályaelem adódik.
A dolgozatom gerincét adó fejezetben részletesen ismertetem a három év mérésein
alapuló eredményeket. Először a fedési kettőscsillagokat tárgyalom, majd következnek
a legfontosabb kutatási eredményekhez vezető ![]() Scuti-típusú pulzáló változócsillagok.
Többségük monoperiodikus, nagy amplitúdójú
Scuti-típusú pulzáló változócsillagok.
Többségük monoperiodikus, nagy amplitúdójú ![]() Scuti csillag, melyeknél
a hosszútávú periódusváltozás természetének megrajzolása, illetve frissítése
volt a cél.
Scuti csillag, melyeknél
a hosszútávú periódusváltozás természetének megrajzolása, illetve frissítése
volt a cél.
Egyes csillagoknál a periódus állandóságát, más esetekben lassú, evolúciós változását
találtuk. Egy esetben kimutattunk a pulzáció kétmodusú jellegét, két esetben
pedig a fény-idő effektust mutató ![]() diagramot diszkutáljuk. A sort a többszörösen
periodikus V784 Cassiopeae
diagramot diszkutáljuk. A sort a többszörösen
periodikus V784 Cassiopeae ![]() Scuti csillag zárja, ahol hat frekvenciát
sikerült azonosítani a fényváltozásban.
Scuti csillag zárja, ahol hat frekvenciát
sikerült azonosítani a fényváltozásban.
Bevezetés
Az OW Geminorum fényváltozását D.H.Kaiser fedezte fel 1988-ban (Kaiser és munkatársai 1988). Fénygörbéje alapján kiderült, hogy fedési változó, ezen belül is a hosszú periódusú Algol-típusú fedési kettősök csoportjába sorolható. Fényessége 8,2 és 10,0 magnitúdó között változik kb. 3,5 éves periódussal. A mély főminimum durván két hétig tart. Mellékminimumát először 1989-ben mérték ki (Williams 1989). A felfedezése óta két főminimumot detektáltak, egyet 1991-ben és egyet 1995-ben. A legalaposabb vizsgálatot Griffin és Duquennoy (1993) végezte. A rendszer érdekessége nagy excentricitása (e=0,55), amelynek következtében a mellékminimum 0,25 fázisnál jelentkezik a főminimum után.
Többszín-fotometriával nagyon kevés mérés, átfogó jellemzés pedig egyáltalán nem történt a rendszerről. A legutóbbi, hazánkból is észlelhető főminimuma 2002 elejére esett. Így nemcsak a minimum kimérését tűztük ki célul, hanem igyekeztünk minél szélesebbkörű vizsgálatokat végezni többszín-fotometriával.
A mérés
A mérések két helyen történtek 2001. december 17. és 2002. január 11. között.
Négy éjszakányi mérés készült a Szegedi Csillagvizsgáló 40 cm-es távcsövével,
kilenc éjszakányi mérés pedig a Piszkéstetői Obszervatórium 60 cm-es távcsövével.
Mindkét műszerrel BV(RI)![]() szűrőkön keresztül készültek a képek. A használt
expozíciós idők 2 és 60 másodperc között változtak az időjárástól és attól függően,
hogy a képek melyik szűrőn keresztül készültek. A 6. táblázat foglalja össze
a mért éjszakák színhelyét, valamint a használt szűrőket.
szűrőkön keresztül készültek a képek. A használt
expozíciós idők 2 és 60 másodperc között változtak az időjárástól és attól függően,
hogy a képek melyik szűrőn keresztül készültek. A 6. táblázat foglalja össze
a mért éjszakák színhelyét, valamint a használt szűrőket.
| dátum | pontok száma | obsz., műszer |
| 2001.12.17. | 1 | Sz 40, CCD BVRI |
| 2001.12.22. | 1 | Pi 60, CCD BVRI |
| 2001.12.23. | 1 | Pi 60, CCD BVRI |
| 2001.12.24. | 1 | Pi 60, CCD R |
| 2001.12.28. | 1 | Pi 60, CCD BV |
| 2001.12.30. | 1 | Pi 60, CCD BV |
| 2001.12.31. | 1 | Pi 60, CCD BVRI |
| 2002.01.01. | 1 | Pi 60, CCD BVRI |
| 2002.01.02. | 1 | Pi 60, CCD BVRI |
| 2002.01.03. | 2 | Sz 40, CCD BVRI |
| 2002.01.04. | 2 | Sz 40, CCD BVRI |
| 2002.01.06. | 1 | Sz 40, CCD BVRI |
| 2002.01.10. | 1 | Pi 60, CCD BVI |
| 2002.01.11. | 1 | Pi 60, CCD BVI |
Az eredmények
Az apertúra-fotometriához használt összehasonlító csillagok a következők voltak:
Összehasonlító csillag: GSC 1332-0578, V=9
![]() 90
90
Ellenőrző csillag: SAO 95777, V=9
![]() 05
05
2001. december 17-én hat órán keresztül B szűrővel méréseket végeztem abból a célból, hogy rövid időskálájú változásokat keressek az OW Geminorum fényességében. Az így kapott adatok azt sejtették - bár nem mutatták ki egyértelműen -, hogy a látómezőben a változó utáni legfényesebb csillag (SAO 95777) fényessége változik. Később a Piszkéstetői Obszervatóriumban készült mérések azt igazolták, hogy nem mutat változást. A hibák minimalizálása érdekében úgy láttuk biztosabbnak, ha mégsem ezt a csillagot használjuk összehasonlítóként, hanem a látómező harmadik legfényesebb csillagát (GSC 1332-0578).
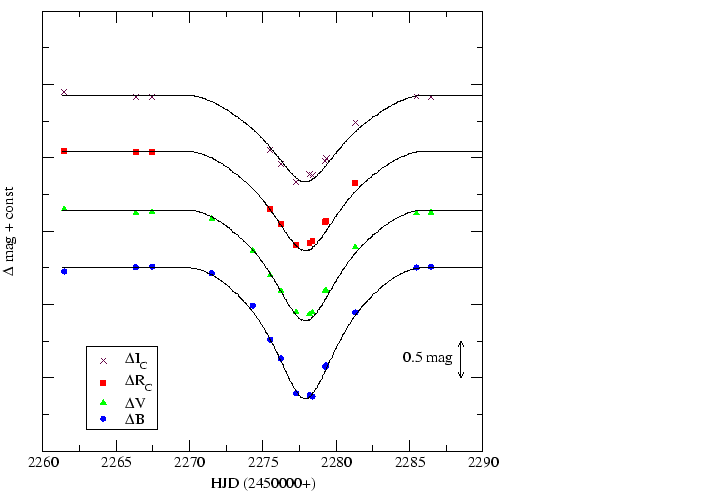
A mindkét műszerre vonatkozó standard transzformációs együtthatók (l. 4. fejezet) meghatározása után az instrumentális magnitúdókat áttranszformáltam és az így kapott fénygörbe látható az 5. ábrán.
Mint már korábban említettem, az OW Geminorumról nincs az irodalomban többszín-fotometriai
vizsgálat. Célunk az volt, hogy a fedési görbe modellezésével megbecsüljük a
komponensek paramétereit, majd ezeket összevessük Griffin és Duquennoy (1993)
eredményeivel. Ők a főkomponenst F2 Ia-II, a mellékkomponenst G8 spektráltípusúnak
határozták meg. Ezen kívül megadták a komponensek sugarait (R![]() =30R
=30R![]() és
R
és
R![]() =35R
=35R![]() ), a mellékkomponens látóirányra merőleges sebességét a
főkomponenshez viszonyítva (v=66 km s
), a mellékkomponens látóirányra merőleges sebességét a
főkomponenshez viszonyítva (v=66 km s![]() ), valamint az ütközési (impakt)
paramétert (10R
), valamint az ütközési (impakt)
paramétert (10R![]() ), amely a két csillag látszó korongátmérőjének fedés
közben fellépő minimális távolsága.
), amely a két csillag látszó korongátmérőjének fedés
közben fellépő minimális távolsága.
Fénygörbemodelleket számítottunk a témavezetőm által írt program segítségével.
A program a csillagok geometriai paramétereit, a relatív mozgásukat, az impakt
paramétert, valamint a szélsötétedést figyelembevéve számolta ki a fedés fénygörbéjét.
A csillagkomponensek hőmérsékleteteit változtatva állítottunk elő olyan modell
fénygörbét, amely leginkább illeszkedik a méréseinkre (5. ábra). Jól látszik,
hogy a mért fénygörbén aszimmetria figyelhető meg, amelynek oka lehet például
foltosság, de meg kell jegyeznem, hogy az aszimmetria realitása kétséges a kevés
fénygörbepont miatt. A számításban használt hőmérsékletek T![]() =7000
=7000![]() 100
K, T
100
K, T![]() =4900
=4900![]() 100 K. Az ennek megfelelő luminozitások L
100 K. Az ennek megfelelő luminozitások L![]() 1950
L
1950
L![]() , L
, L![]() 640 L
640 L![]() , az ebből adódó abszolút fényességek
pedig M
, az ebből adódó abszolút fényességek
pedig M![]() =
=![]() 3
3
![]() 5, M
5, M![]() =
=![]() 2
2
![]() 0. Ennek megfelelően a főkomponens
F2-3 Ib-II, a mellékkomponens G4-5 IIb spektráltípusú. Az így kapott paraméterek
jó egyezést mutatnak Griffin és Duquennoy (1993) eredményeivel, a kis eltérés
még hibahatáron belül van.
0. Ennek megfelelően a főkomponens
F2-3 Ib-II, a mellékkomponens G4-5 IIb spektráltípusú. Az így kapott paraméterek
jó egyezést mutatnak Griffin és Duquennoy (1993) eredményeivel, a kis eltérés
még hibahatáron belül van.
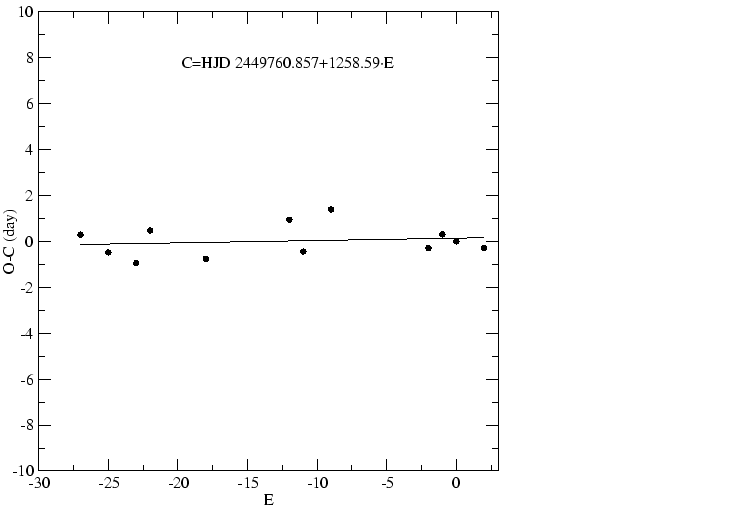
A periódus pontosítása céljából elkészítettem a rendszer ![]() diagramját (6.
ábra). A négy szűrővel készült fénygörbére ötödfokú polinomot illesztve meghatároztam
a minimumidőpontokat és ezek számtani közepéből képeztem az
diagramját (6.
ábra). A négy szűrővel készült fénygörbére ötödfokú polinomot illesztve meghatároztam
a minimumidőpontokat és ezek számtani közepéből képeztem az ![]() diagramhoz
használt minimumidőpontot, amely a HJD= 2452277,73
diagramhoz
használt minimumidőpontot, amely a HJD= 2452277,73![]() 0,2 nap, az ehhez tartozó
0,2 nap, az ehhez tartozó
![]() érték
érték ![]() 0,29 nap. Az
0,29 nap. Az ![]() diagramot a következő efemerissel számoltam
(Hager 1995):
diagramot a következő efemerissel számoltam
(Hager 1995):
Az ![]() diagram pontjai egy zérus meredekségű egyenes körül szórnak. Ez azt
jelenti, hogy a használt periódusérték jó volt, a mérésekből nem lehet nagyobb
pontossággal meghatározni a periódust, tehát a rendszer 1258,59 nap alatt járja
körül a tömegközéppontját. A következő mellékminimum 2002. november elején várható,
többszín-fotometriai mérését tervezzük. Ezeket az eredményeket az Information
Bulletin on Variable Stars 5239-es számában publikáltuk (Derekas és munkatársai
2002b).
diagram pontjai egy zérus meredekségű egyenes körül szórnak. Ez azt
jelenti, hogy a használt periódusérték jó volt, a mérésekből nem lehet nagyobb
pontossággal meghatározni a periódust, tehát a rendszer 1258,59 nap alatt járja
körül a tömegközéppontját. A következő mellékminimum 2002. november elején várható,
többszín-fotometriai mérését tervezzük. Ezeket az eredményeket az Information
Bulletin on Variable Stars 5239-es számában publikáltuk (Derekas és munkatársai
2002b).
Bevezetés
Mindkét rendszer a W-UMa típusú kontakt kettősök osztályába tartozik.
Az SW Lacertae fényváltozását Miss Ashall fedezte fel. Azóta nagyon sok fotografikus,
vizuális és fotoelektromos mérés készült róla, így nagyon jól ismert fénygörbéje
az optikai tertományban, de a közeli infravörösben is készültek mérések a rendszerről.
Fényessége a főminimumban 0
![]() 8-s, mellékminimumban 0
8-s, mellékminimumban 0
![]() 6-s amplitúdóval
változik 0,32 napos (
6-s amplitúdóval
változik 0,32 napos (![]() 8 óra) periódussal. A fénygörbén időnként 0
8 óra) periódussal. A fénygörbén időnként 0![]() 1-0
1-0![]() 2-s
szabálytalanságokat, aszimmetriákat figyeltek meg, amely azt sugallta, hogy
a felszínén foltok találhatók. Dugan és Wright (1939) határozta meg az orbitális
periódust. Panchatsaram és Abhyankar (1981) úgy találta, hogy az
2-s
szabálytalanságokat, aszimmetriákat figyeltek meg, amely azt sugallta, hogy
a felszínén foltok találhatók. Dugan és Wright (1939) határozta meg az orbitális
periódust. Panchatsaram és Abhyankar (1981) úgy találta, hogy az ![]() diagram
két szinusszal illeszthető, így a fény-idő effektust feltételezésével az SW
Lacetae négyes rendszert alkot. A feltételezett harmadik és negyedik komponens
pályaperiódusa 19,67 és 70,25 év. Ezt az elképzelést azonban nem mindenki fogadja
el a rendszerrről, például Borkovits és Hegedüs (1996) szerint nem valószínű
a fény-idő effektus léte.
diagram
két szinusszal illeszthető, így a fény-idő effektust feltételezésével az SW
Lacetae négyes rendszert alkot. A feltételezett harmadik és negyedik komponens
pályaperiódusa 19,67 és 70,25 év. Ezt az elképzelést azonban nem mindenki fogadja
el a rendszerrről, például Borkovits és Hegedüs (1996) szerint nem valószínű
a fény-idő effektus léte.
Az AB Andromedae Guthnick és Prager által 1927-ben felfedezett W UMa-típusú
változócsillag. Fényessége főminimumban 0
![]() 9-s, mellékminimumban 0
9-s, mellékminimumban 0
![]() 6-s
amplitúdóval változik 0,33 napos (
6-s
amplitúdóval változik 0,33 napos (![]() 8 óra) periódussal. Periódusváltozását
Oosterhoff (1950) és Binnendijk (1959) tárgyalták először. Fénygörbéje minimum
környékén aszimmetriát, maximumban pedig torzulásokat mutat, amelyet gázáramlások
megjelenésének (Kalchaev és Trutse 1965) vagy foltaktivitásnak (például Bell
és munkatársai 1984) tulajdonítanak. Periódusváltozásait a nagyobb tömegű csillagról
a kisebb tömegű felé történő anyagátadással, a fény-idő effektussal, illetve
a főkomponens mágneses aktivitásával magyarázzák. Ez a rendszer is nagyon közkedvelt,
az irodalomban rengeteg mérési eredmény található.
8 óra) periódussal. Periódusváltozását
Oosterhoff (1950) és Binnendijk (1959) tárgyalták először. Fénygörbéje minimum
környékén aszimmetriát, maximumban pedig torzulásokat mutat, amelyet gázáramlások
megjelenésének (Kalchaev és Trutse 1965) vagy foltaktivitásnak (például Bell
és munkatársai 1984) tulajdonítanak. Periódusváltozásait a nagyobb tömegű csillagról
a kisebb tömegű felé történő anyagátadással, a fény-idő effektussal, illetve
a főkomponens mágneses aktivitásával magyarázzák. Ez a rendszer is nagyon közkedvelt,
az irodalomban rengeteg mérési eredmény található.
A mérés
Az SW Lacertae méréseit 2001. október 7. és 14. között négy éjszakán át végeztem Johnson-féle VRI szűrőkkel a Szegedi Csillagvizsgáló 40 cm-es távcsövével. V szűrővel 15 másodperces, R és I szűrővel 10 másodperces expozíciós időt használtam. A mérési adatok paraméterei a 7. táblázatban találhatóak.
| dátum | pontok | obsz., műszer |
| 2001.10.07. | 931 | Sz 40, CCD VRI |
| 2001.10.12. | 1070 | Sz 40, CCD VRI |
| 2001.10.13. | 1130 | Sz 40, CCD VRI |
| 2001.10.14. | 1349 | Sz 40, CCD VRI |
Az AB Andromedae megfigyelései 2001. október 22. és 27. között történtek három éjszakán keresztül, szintén Johnson-féle VRI szűrőkkel a Szegedi Csillagvizsgáló 40 cm-es távcsövével. A képek átlagosan 15 és 20 másodperces expozíciós idővel készültek. A mérési pontok számát a 8. táblázat tartalmazza.
| dátum | pontok | obsz., műszer |
| 2001.10.22. | 586 | Sz 40, CCD VRI |
| 2001.10.23. | 717 | Sz 40, CCD VRI |
| 2001.10.27. | 828 | Sz 40, CCD VRI |
Az eredmények
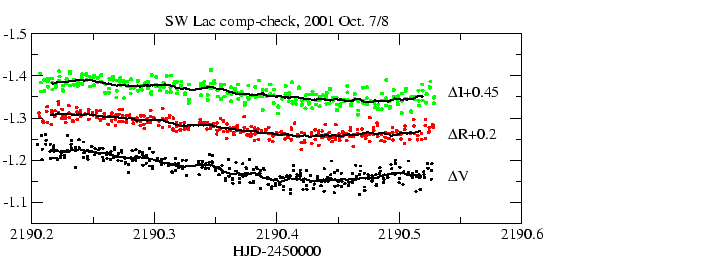
Az SW Lacertae fénygörbéjének kiméréséhez két közeli csillagot használtam összehasonlítóként:
Összehasonlító csillag: GSC 3215-1586.
Ellenőrző csillag: GSC 3215-0906.
A kiértékelésnél ezen csillagok differenciális fénygöbéje első közelítésben
nem mutatkozott konstansnak (7. ábra), de ennek eldöntésére további mérésre
volt szükség, hosszabb expozíciós idővel, hogy több halvány mezőcsillagot lehessen
összehasonlítóként felhasználni. Erre 2001. december 8-án került sor. Kiderült,
hogy az ellenőrző csillagként használt GSC 3215-0906 számú csillag fényessége
változik, kb. 0![]() 05-s amplitúdóval. Típus szerinti besorolása ezen egy éjszakás
mérés alapján nem lehetséges, ehhez szükséges a csillag további észlelése.
05-s amplitúdóval. Típus szerinti besorolása ezen egy éjszakás
mérés alapján nem lehetséges, ehhez szükséges a csillag további észlelése.
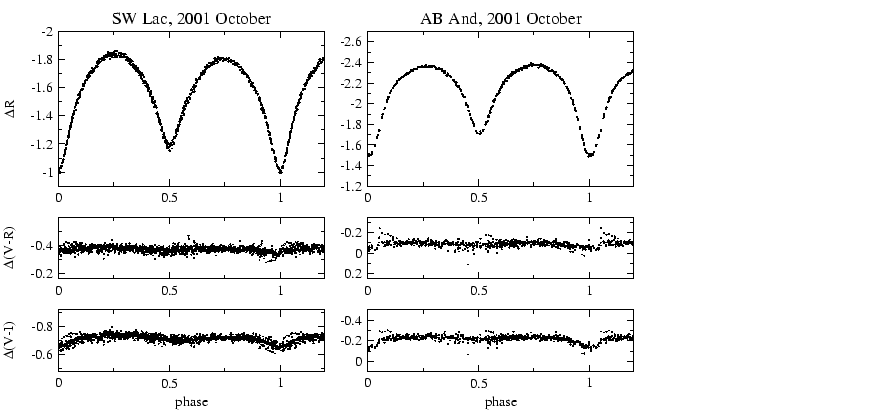
Ezután standard transzformáltam az instrumentális fényességértékeket. Az így
kapott ![]() R fénygörbe és a színindexek görbéje a 8. ábrán látható a bal
oldali paneleken.
R fénygörbe és a színindexek görbéje a 8. ábrán látható a bal
oldali paneleken.
Az AB Andromedae használt összehasonlító csillagai:
Összehasonlító csillag: GSC 2763-0683
Ellenőrző csillag: GSC 2763-0878
Itt nem tapasztaltam olyan fényességváltozást, ami meghaladná a ![]() 0
0
![]() 02-s
szintet, ami a mérések pontosságának nagyságrendje.
02-s
szintet, ami a mérések pontosságának nagyságrendje.
A standard transzformált fény- és színgörbék a 8. ábra jobb oldali panelein láthatók.
Az ![]() diagram elkészítéséhez mindkét csillag esetében a fénygörbék minimumhoz
közeli szegmenseire alacsony fokszámú polinomot illesztettem és ennek minimumidőpontját
határoztam meg. A 9. táblázatban az AB Andromedae, a 10. táblázatban az SW Lacertae
új minimumértékeit sorolom fel.
diagram elkészítéséhez mindkét csillag esetében a fénygörbék minimumhoz
közeli szegmenseire alacsony fokszámú polinomot illesztettem és ennek minimumidőpontját
határoztam meg. A 9. táblázatban az AB Andromedae, a 10. táblázatban az SW Lacertae
új minimumértékeit sorolom fel.
| MJD |
min. típus | szűrő | MJD |
min. típus | szűrő |
| 52205,3339 | I | R | 52206,4979 | II | R |
| 52205,3345 | I | I | 52206,4980 | II | V |
| 52205,3350 | I | V | 52206,4986 | II | I |
| 52205,5014 | II | I | 52210,3147 | I | V |
| 52205,5029 | II | R | 52210,3151 | I | I |
| 52205,5036 | II | V | 52210,3154 | I | R |
| 52206,3324 | I | I | 52210,4800 | II | I |
| 52206,3326 | I | V | 52210,4808 | II | V |
| 52206,3329 | I | R | 52210,4811 | II | R |
| MJD |
min. típus | szűrő | MJD |
min. típus | szűrő |
| 52190,3326 | I | V | 52196,2653 | II | I |
| 52190,3329 | I | I | 52196,2660 | II | V |
| 52190,3331 | I | R | 52196,2662 | II | R |
| 52190,4932 | II | I | 52196,4255 | I | I |
| 52190,4936 | II | V | 52196,4256 | I | V |
| 52190,4937 | II | R | 52196,4266 | I | R |
| 52195,3037 | II | V | 52197,2274 | II | V |
| 52195,3040 | II | R | 52197,2279 | II | R |
| 52195,3043 | II | I | 52197,2280 | II | I |
| 52195,4636 | I | I | 52197,3869 | I | V |
| 52195,4637 | I | V | 52197,3880 | I | R |
| 52195,4651 | I | R | 52197,3885 | I | I |
Az SW Lacertae ![]() diagramjának kiszámításához a következő efemerist használtam
(Pribulla és munkatársai 1999):
diagramjának kiszámításához a következő efemerist használtam
(Pribulla és munkatársai 1999):
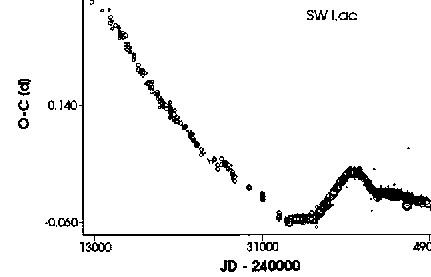
Az ![]() diagramot csak az utolsó tíz év eredményeire számoltam, mert csak azt
kívántam megvizsgálni, hogy az utóbbi időben mutatkozott-e változás a rendszer
periódusában. Évtizedes időskálán a rendszer periódusa folyamatosan változik
(9. ábra), az utóbbi időben pedig folyamatos perióduscsökkenés figyelhető meg.
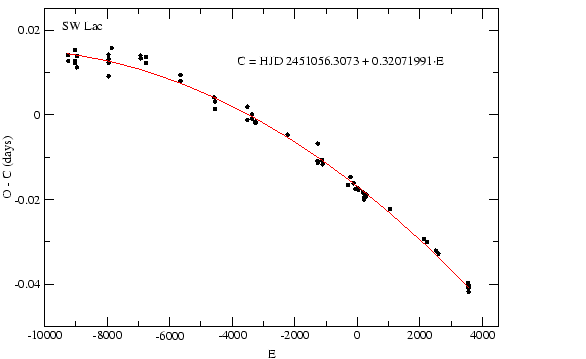
Ezt jól mutatja az elmúlt tíz év parabolikus diagramja (10. ábra). Az illesztett
parabolából a periódusváltozás mértéke meghatározható, amely a következő formulával
írható le:
diagramot csak az utolsó tíz év eredményeire számoltam, mert csak azt
kívántam megvizsgálni, hogy az utóbbi időben mutatkozott-e változás a rendszer
periódusában. Évtizedes időskálán a rendszer periódusa folyamatosan változik
(9. ábra), az utóbbi időben pedig folyamatos perióduscsökkenés figyelhető meg.
Ezt jól mutatja az elmúlt tíz év parabolikus diagramja (10. ábra). Az illesztett
parabolából a periódusváltozás mértéke meghatározható, amely a következő formulával
írható le:
Az elkövetkező évekre kiszámítottam a minimumidőpontok előrejelzésére szolgáló
kvadratikus efemerist, melynek alakja:
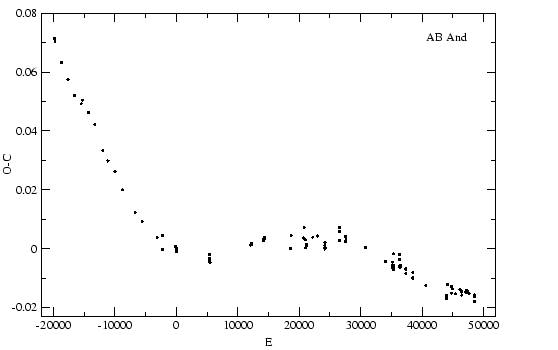
Az AB Andromedae esetén összegyűjtöttem az irodalomból az összes fellelhető
minimumidőpontot, amelyből elkészítettem az ![]() diagramját (12. ábra). A következő
efemerist használtam (Nellermoe és Reitzler 1997):
diagramját (12. ábra). A következő
efemerist használtam (Nellermoe és Reitzler 1997):
A diagram utolsó szakasza alapján elmondható, hogy a rendszer az utóbbi negyven évben közel konstans periódust mutatott, amelyre rárakódik egy lehetséges fény-idő effektus okozta egy hullámzás. Ennek vizsgálatát Borkovits és Hegedüs (1996) közölték.
Ha megvizsgáljuk a két csillag fénygörbéit, azt tapasztaljuk, hogy maximumaik
között különbségek figyelhetők meg. Ez arra utal, hogy világos, vagy sötét foltok
vannak jelen a csillagon, melyek módosítják a pusztán geometriai eredetű fényváltozásokat.
Az SW Lacertae esetén V-ben, ![]() -ben,
-ben, ![]() -ben rendre 0
-ben rendre 0
![]() 05, 0
05, 0
![]() 04,
0
04,
0
![]() 03-s különbségek voltak megfigyelhetőek. Ezen kívül a minimumok alakjai
is aszimmetriát mutatnak, amit szintén okozhat foltosság. Korábbi vizsgálatokban
a maximumbeli különbségek elérték a 0,1 magnitúdót is. Ebből arra következtethetünk,
hogy jelenleg kisebb lehet a foltaktivitás, illetve, hogy nem látunk rá a foltokra.
03-s különbségek voltak megfigyelhetőek. Ezen kívül a minimumok alakjai
is aszimmetriát mutatnak, amit szintén okozhat foltosság. Korábbi vizsgálatokban
a maximumbeli különbségek elérték a 0,1 magnitúdót is. Ebből arra következtethetünk,
hogy jelenleg kisebb lehet a foltaktivitás, illetve, hogy nem látunk rá a foltokra.
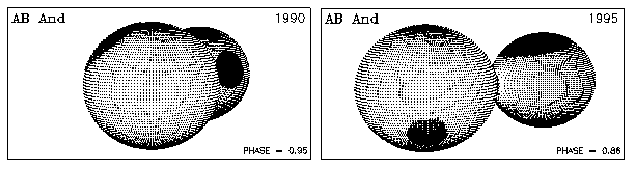
Az AB Andromedae fénygörbéin is megfigyelhetőek a maximumok közti különbségek,
valamint az aszimmetriák, bár kisebb mértékben. V-ben 0
![]() 02,
02, ![]() -ben
0
-ben
0
![]() 02,
02, ![]() -ben 0
-ben 0
![]() 01. Ez is a csillag foltosságára utal. A fénygörbék
alakja hasonló Djuraševic és munkatársai (2000) analízisében szereplő
1990-es fénygörbék alakjához. A 11. ábrán mutatom meg az ahhoz tartozó illesztett
foltmodellt, ami pusztán a fénygörbék jellegzetessége alapján valószínűleg nagyon
hasonlít a 2001-es állapothoz. Jelen munkám nem terjedt ki a foltillesztésre,
terveim szerint a későbbiekben foglalkozom a kérdéssel.
01. Ez is a csillag foltosságára utal. A fénygörbék
alakja hasonló Djuraševic és munkatársai (2000) analízisében szereplő
1990-es fénygörbék alakjához. A 11. ábrán mutatom meg az ahhoz tartozó illesztett
foltmodellt, ami pusztán a fénygörbék jellegzetessége alapján valószínűleg nagyon
hasonlít a 2001-es állapothoz. Jelen munkám nem terjedt ki a foltillesztésre,
terveim szerint a későbbiekben foglalkozom a kérdéssel.
Ezeket az eredményeket az Information Bulletin on Variable Stars 5255-ös számában publikáltuk (Derekas és munkatársai 2002a)
A pulzáló változócsillagok számos típusa közül a rövid periódusú, I. populációs
nagyamplitúdójú ![]() Scuti-típusú és ennek II. populációs megfelelőjével,
az SX Phoenicis-típusú változókkal foglalkoztam. Az általam mért nyolc pulzáló
változócsillag periódusa általában 0,1 naphoz közeli. Legtöbbjüknél a közvetlen
cél a hosszútávú periódusváltozás vizsgálata volt.
Scuti-típusú és ennek II. populációs megfelelőjével,
az SX Phoenicis-típusú változókkal foglalkoztam. Az általam mért nyolc pulzáló
változócsillag periódusa általában 0,1 naphoz közeli. Legtöbbjüknél a közvetlen
cél a hosszútávú periódusváltozás vizsgálata volt.
Bevezetés
Az YZ Bootis változását a Sonnebergi Obszervatórium munkatársa, Cuno Hoffmeister
fedezte fel 1949-ben. Fényességét ![]() 0
0
![]() 4-s amplitúdóval változtatja
0,1 napos (2,4 óra) periódussal. Az első periódusmeghatározást Eggen (1955)
végezte fotoelektromos mérésekkel, aki úgy találta, hogy közel 2,5 órás periódussal
változik a csillag fényessége. 1958 és 1979 között számos mérés készült a csillagról.
Ezek közül kiemelném Heiser és Hardie (1964) mérését, amelyben arról számolnak
be, hogy a fénygörbe felszálló ágán ciklusonként kis változások figyelhetők
meg. Hasonló megfigyelésről számolt be Gieren és munkatársai (1974). Szeidl
és Mahdy (1981) vizsgálta utoljára a periódusváltozását, ők folyamatos perióduscsökkenést
állapítottak meg. Joner és McNamara (1983) végezte a csillag átfogó fotometriai
és spekroszkópiai vizsgálatát, melyben meghatározták a fizikai paramétereket.
Ők a periódust konstansnak találták. Az azóta eltelt közel húsz évben senki
sem foglalkozott a csillag vizsgálatával, csak mérési eredmények (maximumidőpontok)
találhatók róla az irodalomban. Méréseim célja az volt, hogy megvizsgáljam,
történt-e periódusváltozás azóta.
4-s amplitúdóval változtatja
0,1 napos (2,4 óra) periódussal. Az első periódusmeghatározást Eggen (1955)
végezte fotoelektromos mérésekkel, aki úgy találta, hogy közel 2,5 órás periódussal
változik a csillag fényessége. 1958 és 1979 között számos mérés készült a csillagról.
Ezek közül kiemelném Heiser és Hardie (1964) mérését, amelyben arról számolnak
be, hogy a fénygörbe felszálló ágán ciklusonként kis változások figyelhetők
meg. Hasonló megfigyelésről számolt be Gieren és munkatársai (1974). Szeidl
és Mahdy (1981) vizsgálta utoljára a periódusváltozását, ők folyamatos perióduscsökkenést
állapítottak meg. Joner és McNamara (1983) végezte a csillag átfogó fotometriai
és spekroszkópiai vizsgálatát, melyben meghatározták a fizikai paramétereket.
Ők a periódust konstansnak találták. Az azóta eltelt közel húsz évben senki
sem foglalkozott a csillag vizsgálatával, csak mérési eredmények (maximumidőpontok)
találhatók róla az irodalomban. Méréseim célja az volt, hogy megvizsgáljam,
történt-e periódusváltozás azóta.
A mérés
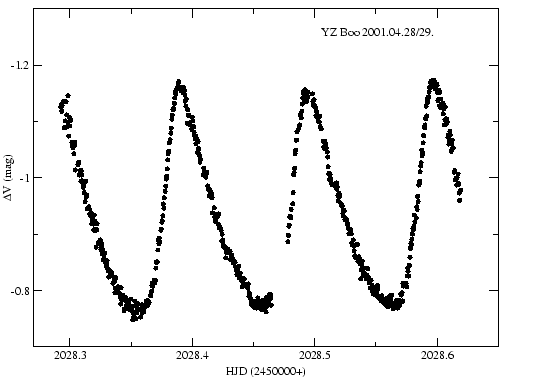
Megfigyeléseimet 2001 tavaszán hat éjszakán át végeztem Johnson-féle V szűrővel a Szegedi Csillagvizsgáló 40 cm-es távcsövével. A képek 15 és 40 másodperces expozíciós idővel készültek. A 2001. április 28-i éjszaka fénygörbéje a 13. ábrán látható. Összehasonlító csillagként a 6 ívperces látómező másik fényes csillagát, a GSC 2568-1184-t használtam. A mérésekről összefoglaló a 11. táblázatban található.
| dátum | pontok | obsz., műszer |
| 2001.03.16. | 279 | Sz 40, CCD V |
| 2001.04.01. | 536 | Sz 40, CCD V |
| 2001.04.25. | 177 | Sz 40, CCD V |
| 2001.04.28. | 697 | Sz 40, CCD V |
| 2001.04.30. | 526 | Sz 40, CCD V |
| 2001.05.09. | 307 | Sz 40, CCD V |
Az eredmények
A periódus vizsgálatához elkészítettem a csillag ![]() diagramját. Ehhez összegyűjtöttem
az irodalomban megtalálható összes maximumidőpontot és kiegészítettem a saját
méréseimből származó maximumidőpontokkal. Hat éjszakányi mérésből (tíz periódus
fénygörbéjét sikerült felvenni) tíz új maximumidőpontot tudtam meghatározni
(12. táblázat). A fénygörbékből a maximum idejét alacsony fokszámú polinom illesztésével
és annak szélsőértékének meghatározásával végeztem. Az
diagramját. Ehhez összegyűjtöttem
az irodalomban megtalálható összes maximumidőpontot és kiegészítettem a saját
méréseimből származó maximumidőpontokkal. Hat éjszakányi mérésből (tíz periódus
fénygörbéjét sikerült felvenni) tíz új maximumidőpontot tudtam meghatározni
(12. táblázat). A fénygörbékből a maximum idejét alacsony fokszámú polinom illesztésével
és annak szélsőértékének meghatározásával végeztem. Az ![]() diagram (14. ábra)
kiszámításához a következő efemerist használtam (epocha: Joner és McNamara 1983,
periódus: Hipparcos adatbázis):
diagram (14. ábra)
kiszámításához a következő efemerist használtam (epocha: Joner és McNamara 1983,
periódus: Hipparcos adatbázis):
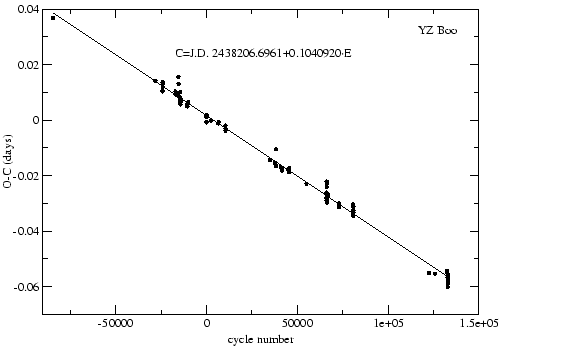
Az így kapott ![]() diagramra egy
diagramra egy
![]() meredekségű
egyenes illeszthető. Ez azt jelenti, hogy a periódus nem változik, csak rossz
periódusértékkel számoltam az
meredekségű
egyenes illeszthető. Ez azt jelenti, hogy a periódus nem változik, csak rossz
periódusértékkel számoltam az ![]() diagramot. A helyes periódus úgy kapható
meg, hogy a használt periódusból levonjuk az egyenes meredekségét. Így a következő
periódusértéket kaptam:
diagramot. A helyes periódus úgy kapható
meg, hogy a használt periódusból levonjuk az egyenes meredekségét. Így a következő
periódusértéket kaptam:
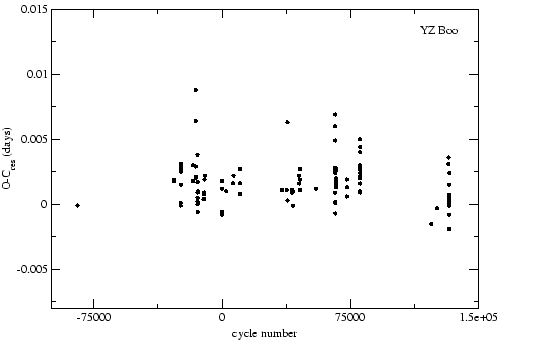
Ezzel új efemeris adható meg a további periódusvizsgálatokhoz:
| 1985,6116 | 2028,5975 | ||
| 2001,5381 | 2030,3693 | ||
| 2025,3695 | 2030,4726 | ||
| 2028,3902 | 2030,5759 | ||
| 2028,4946 | 2039,3221 |
Bevezetés
Fényváltozását Hoffmeister fedezte fel fotografikus úton 1942-ben és mint RRc
változót klasszifikálta. Efemerist is megadott:
Azután számos fotografikus és spektroszkópiai mérés készült róla a 60-as, 70-es években. De Bruyn (1972) Walraven-féle rendszerrel öt színben készített fotoelektromos méréseket, melyekből új periódust határozott meg 0,14952 napban. A V567 Ophiuchiról az irodalomban utoljára megjelent cikket Powell és munkatársai (1990) publikálta. Ebben a cikkben fotometriai és spektroszkópiai mérésekből meghatározták a csillag olyan alapvető paramétereit, mint az effektív hőmérséklet, felszíni gravitáció, kémiai összetétel, radiális sebességgörbe, sugár, abszolút fényesség, távolság, tömeg. Ezen cikk óta nem végeztek újabb vizsgálatot a V567 Ophiuchira.
A mérés
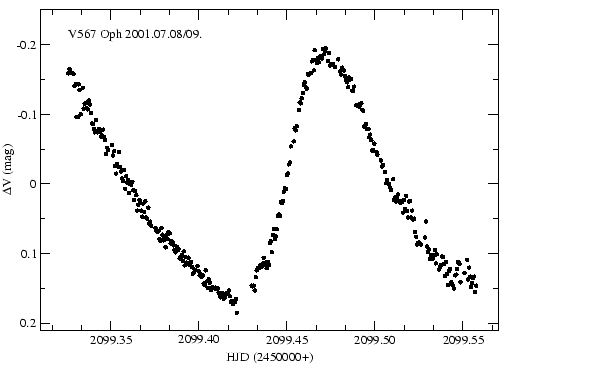
A feldolgozott méréseket kérésemre Mészáros Szabolcs harmadéves csillagász hallgató, valamint jómagam 2001 júliusában és augusztusában 10 éjszakán keresztül végeztük. A képek 30, 45 másodperces expozíciós idővel készültek az időjárásnak megfelelően a Szegedi Csillagvizsgáló 40 cm-es műszerével Johnson-féle V szűrőn keresztül. A mérési pontok száma az egyes éjszakákon a 13. táblázatban találhatók.
| dátum | pontok száma | obsz.,műszer |
| 2001.07.07. | 329 | Sz 40, CCD V |
| 2001.07.08. | 349 | Sz 40, CCD V |
| 2001.07.14. | 242 | Sz 40, CCD V |
| 2001.07.15. | 205 | Sz 40, CCD V |
| 2001.07.20. | 48 | Sz 40, CCD V |
| 2001.08.03. | 209 | Sz 40, CCD V |
| 2001.08.04. | 266 | Sz 40, CCD V |
| 2001.08.12. | 359 | Sz 40, CCD V |
| 2001.08.15. | 176 | Sz 40, CCD V |
| 2001.08.16. | 112 | Sz 40, CCD V |
Az eredmények
Az CCD képek kimérése után a kapott fénygörbékből (egyet mutatok be példaképpen
a 16. ábrán) alacsony fokszámú polinom illesztésével meghatároztam a fénygörbékből
a maximumidőpontokat (14. táblázat). Az apertúra fotometriához az összehasonlítóként
használt csillagok megegyeznek a Powell és munkatársai (1990) cikkben szereplő
![]() és
és ![]() jelű csillagokkal.
jelű csillagokkal.
| 2098,4246 | 0,0555 | 2125,3480 | 0,0648 |
| 2099,4703 | 0,0545 | 2126,3818 | 0,0519 |
| 2105,4578 | 0,0611 | 2134,3087 | 0,0541 |
| 2106,4952 | 0,0519 | 2138,3497 | 0,0580 |
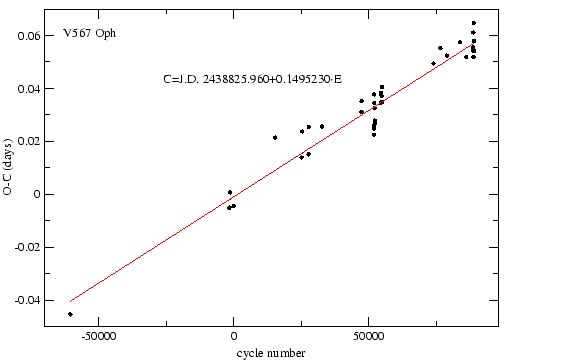
Az irodalomból kigyűjtöttem az összes fellelhető maximumidőpontot. Ezekből a
következő efemeris (GCVS) segítségével elkészítettem a V567 Ophiuchi ![]() diagramját
(17. ábra):
diagramját
(17. ábra):
Az ![]() digramra a következő egyenest lehetett illeszteni:
digramra a következő egyenest lehetett illeszteni:
Ez azt jelenti, hogy a periódus az eddigi mérések során nem változott, csak
nem a helyes periódusértékkel számoltuk ki az ![]() diagramot. A korrekció után
a következő periódusértéket kaptam:
diagramot. A korrekció után
a következő periódusértéket kaptam:
A fenti meggondolások realitását azonban megkérdőjelezte az ![]() diagram korrekciója
után maradt pontok viszonylag nagy szórása. A 18. ábrán jól látszik, hogy
diagram korrekciója
után maradt pontok viszonylag nagy szórása. A 18. ábrán jól látszik, hogy ![]() 0,01
nap szórást mutatnak a pontok, ami túl nagy, hiszen a maximumidőpontok egyedi
hibája a
0,01
nap szórást mutatnak a pontok, ami túl nagy, hiszen a maximumidőpontok egyedi
hibája a ![]() 0,001 nap nagyságrendjébe esik.
0,001 nap nagyságrendjébe esik.
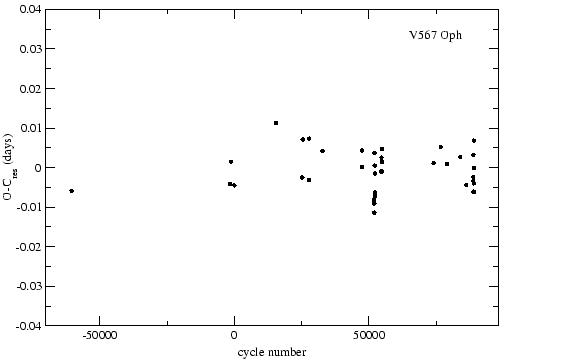
18. ábra: A V567 Ophiuchi perióduskorrekciója után visszamaradt ![]() diagramja
diagramja
Felmerült a lehetőség, hogy esetleg a nagy szórást egy másik gerjesztett módus fénygörbe-torzító hatása okozhatja. Az erre utaló jeleket már Powell és munkatársai (1990) is említette, azon megjegyzéssel, hogy a V567 Ophiuchi fénygörbéje ciklusról ciklusra változni látszott a mérési hibákon túl.
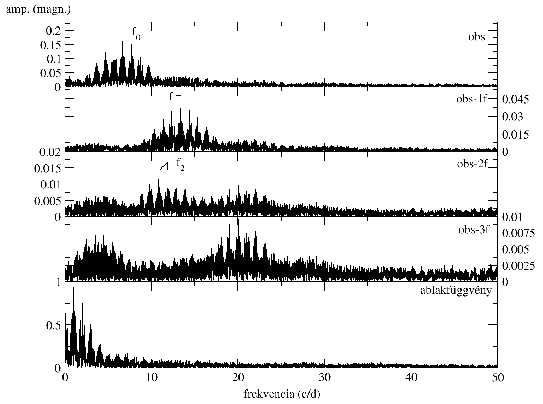
A kérdést a tíz éjszakányi adatsor Fourier-analízisével vizsgáltam meg. Mindehhez
Sperl (1998) Period98 programját használtam. Az eredményül kapott frekvenciákat
a 15. táblázatban foglalom össze. Több lépéses fehérítéssel sorra eltávolítottam
a fénygörbék domináns frekvenciáit, amelyet a 19. ábrán mutatok be. Az első
lépés megadta a csillag fő periódusát, az ![]() =6,68 ciklus/naphoz tartozó
0,1497 napos értékkel. Az ilyen frekvenciájú és Fourier-spektrumból származó
amplitúdójú szinusz levonása után maradt jel frekvencia-spektrumában az
=6,68 ciklus/naphoz tartozó
0,1497 napos értékkel. Az ilyen frekvenciájú és Fourier-spektrumból származó
amplitúdójú szinusz levonása után maradt jel frekvencia-spektrumában az
![]() frekvencia jelenik meg. Ennek az az oka, hogy a fénygörbe nem szinuszos jellegű,
így megjelennek a domináns frekvencia felharmonikusai. Ennek levonása után azonban
megjelenik az
frekvencia jelenik meg. Ennek az az oka, hogy a fénygörbe nem szinuszos jellegű,
így megjelennek a domináns frekvencia felharmonikusai. Ennek levonása után azonban
megjelenik az ![]() =10,82 ciklus/nap és 11,82 ciklus/nap értéknél egy-egy
csúcs. A pontos érték az erős 1 c/d hamis csúcs-szerkezet miatt bizonytalan,
de az
=10,82 ciklus/nap és 11,82 ciklus/nap értéknél egy-egy
csúcs. A pontos érték az erős 1 c/d hamis csúcs-szerkezet miatt bizonytalan,
de az ![]() =10,82 ciklus/nap értéket elfogadva az
=10,82 ciklus/nap értéket elfogadva az
![]() 0,60
arány könnyen értelmezhető, mint a radiális alapmódus és második felhang egyidejű
gerjesztettségének jele (Breger 1979).
0,60
arány könnyen értelmezhető, mint a radiális alapmódus és második felhang egyidejű
gerjesztettségének jele (Breger 1979).
| P (nap) | A (mmag.) | ||
| F |
6,687 | 0,1495 | 162,2 |
| F |
13,376 | 0,0748 | 36,8 |
| F |
11,826 | 0,0846 | 11,8 |
| vagy | |||
| 10,82 | 0,0924 | 11,5 |
Így legfontosabb eredményem a V567 Ophiuchival kapcsolatban, hogy a csillag kétmódusú pulzációt mutat. További méréseket tervezek 2002 nyarán a kérdés további vizsgálatához és esetleg újabb módusok kimutatására.
Bevezetés
Az XX Cygni fényváltozását Ceraski fedezte fel 1904-ben. Fényváltozását 10,7 és 11,6 magnitúdó között, periódusát 3,2 órának határozta meg. Ezután vizuális megfigyelések kezdődtek a csillagról. 1904 és 1911 között több mint 2600 vizuális becslést végeztek és ezekből csaknem 150 maximum időpontot határoztak meg.
Ezután többen is méréssorozatokat végeztek a periódus minél pontosabb meghatározására, többek között Schwab (1906), Graff (1906), Luizet (1908) és Nijland (1911).
Az irodalomban utoljára Szeidl és Mahdy (1981) foglalta össze az XX Cygni periódusának változásait. Arra az eredményre jutottak, hogy 1942-ben ``hirtelen'' változás lépett fel a periódusban. Így az 1942 utáni periódust 0,134865113 napban határozták meg.
Shapley és Shapley (1915) még úgy emlegette az XX Cygnit, mint legrövidebb periódusú változócsillagot, mára már a típusának egyik leghosszabban pulzáló csillaga, holott az elmúlt közel 90 évben nem változott jelentős mértékben a periódusa. Ez is mutatja, hogy nem egész egy évszazad alatt milyen sokat változott ezen csillagok asztrofizikai értelmezése.
A mérés
Az XX Cygni mérését 2000. július 31. és augusztus 3. között három egymást követő éjszakán végeztem Szegeden, a Béke épület tetején elhelyezett 28 cm-es távcsővel. Az egyes képek 20 másodperces expozíciós idővel készültek, szűrő nélkül. Az egyes éjszakákon felvett pontok számát a 16. táblázat tartalmazza.
| dátum | pontok | obsz., műszer |
| 2000.07.31. | 243 | Sz 28, CCD |
| 2000.08.01. | 320 | Sz 28, CCD |
| 2000.08.02. | 263 | Sz 28, CCD |
Az apertúra fotometriához a következő két közeli csillagot használtam összehasonlítóként:
Összehasonlító csillag: GSC 3948-2542, 10
![]() 4
4
Ellenőrző csillag: GSC 3948-2105, 10
![]() 9
9
Ezen összehasonlítók fényességváltozásának szórása kb. 0,015 magnitudó körüli (21. ábra), tehát fényességük a mérési hibán belül állandó volt.
Az összes fénygörbe fázisba rendezve a 20. ábrán látható.
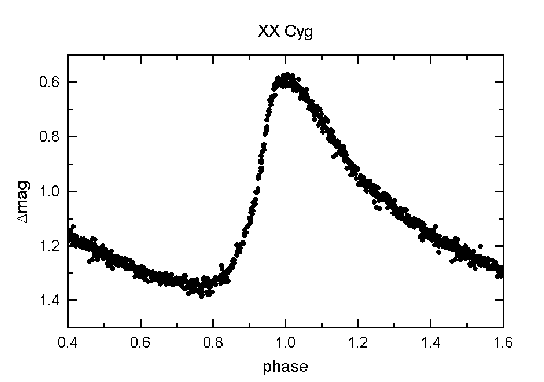
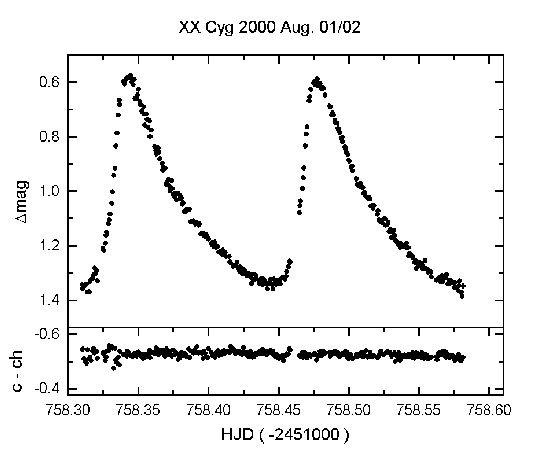
Az XX Cygni egy tipikus fénygörbéje 2000. augusztus 1/2 -án a 21. ábrán látható.
Az eredmények
Az XX Cygni fénygörbéje egyszeresen periodikus, ezért periódusvizsgálatára jól
használható az ![]() diagram. A méréseimből származó öt új maximumidőpont (17.
táblázat) meghatározásához a fénygörbére alacsony fokszámú (3-5) polinomot illesztettem
és ennek maximumidőpontját határoztam meg, amelyekkel kiegészítettem az eddigi
mérésekből származó
diagram. A méréseimből származó öt új maximumidőpont (17.
táblázat) meghatározásához a fénygörbére alacsony fokszámú (3-5) polinomot illesztettem
és ennek maximumidőpontját határoztam meg, amelyekkel kiegészítettem az eddigi
mérésekből származó ![]() diagramot. Az illesztés becsült hibája kb. 0,0003
nap. Az
diagramot. Az illesztés becsült hibája kb. 0,0003
nap. Az ![]() diagram elkészítéséhez az adatokat Szeidl és Mahdy (1981) 1980-ig
bezárulva összegyűjtött munkájából, a későbbieket az irodalomból gyűjtöttem
össze.
diagram elkészítéséhez az adatokat Szeidl és Mahdy (1981) 1980-ig
bezárulva összegyűjtött munkájából, a későbbieket az irodalomból gyűjtöttem
össze.
| MJD | MJD | ||
| 51757,3984 | 0,0088 | 51758,4773 | 0,0088 |
| 51757,5342 | 0,0098 | 51759,4214 | 0,0089 |
| 51758,3432 | 0,0096 |
Az ![]() diagram számításában Szeidl és Mahdy (1981) efemerisét használtam:
diagram számításában Szeidl és Mahdy (1981) efemerisét használtam:
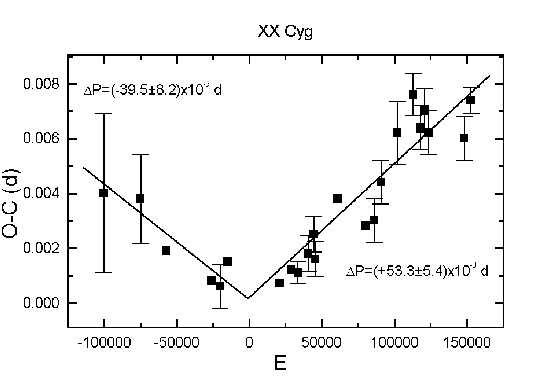
Az XX Cygni ![]() diagramja a 22. ábrán látható.
diagramja a 22. ábrán látható.
Szeidl és Mahdy (1981) vizsgálatukban arra a következtetésre jutottak, hogy
az ![]() diagramra leginkább két egyenes illeszthető, ami azt jelenti, hogy
az XX Cygni periódusában az egyenes törésének időpontjában, 1942-ben hirtelen
ugrás történt, azután a periódus konstans maradt. A periódusváltozás (92,8
diagramra leginkább két egyenes illeszthető, ami azt jelenti, hogy
az XX Cygni periódusában az egyenes törésének időpontjában, 1942-ben hirtelen
ugrás történt, azután a periódus konstans maradt. A periódusváltozás (92,8 ![]() 9,8)
9,8)![]() 10
10![]() nap volt.
nap volt.
Méréseim megerősítették ezt az eredményt. Az egyenes második ágára a következő
kifejezést kaptam:
A hirtelen periódusváltozás okára több magyarázat született az irodalomban. Sweigart és Renzini (1979) szerint az anyag konvektív zónában való áramlásának szabálytalanságaiból ered, úgynevezett ``konvektív túllövések'' okozzák. Breger és Pamyatnikh (1998), valamint Rodríguez és munkatársai (1995) a csillagban fellépő nemlineáris effektusokkal magyarázzák a hirtelen periódusváltozást.
Ezeket az eredményeket az Information Bulletin on Variable Stars 4950-es számában publikáltuk (Kiss és Derekas 2000)
Bevezetés
A DY Pegasi egy sokat mért változócsillag, amely ![]() 0
0
![]() 6-s amplitúdóval
és 0,07 nap (1,6 óra) periódussal változtatja fényességét. Mint változócsillagot
O. Morgenroth fedezte fel 1934-ben. Soloviev (1938) határozta meg először a
fényváltozás periódusát és típusát. Ezután sokan vizsgálták a csillagot. Többen
megfigyelték, hogy a fénygörbék maximumai eltérőek. Grigorevsky és Mandell (1960)
ezt egy 0,2554 napos második periódus jelenlétével értelmezte. A későbbi fotoelektromos
mérések csak kisebb, 0,04 magnitúdós fluktuációkat mutattak a maximumok nagyságában.
Megadták ennek a hosszú időskálájú változásnak a periódusát, amely
6-s amplitúdóval
és 0,07 nap (1,6 óra) periódussal változtatja fényességét. Mint változócsillagot
O. Morgenroth fedezte fel 1934-ben. Soloviev (1938) határozta meg először a
fényváltozás periódusát és típusát. Ezután sokan vizsgálták a csillagot. Többen
megfigyelték, hogy a fénygörbék maximumai eltérőek. Grigorevsky és Mandell (1960)
ezt egy 0,2554 napos második periódus jelenlétével értelmezte. A későbbi fotoelektromos
mérések csak kisebb, 0,04 magnitúdós fluktuációkat mutattak a maximumok nagyságában.
Megadták ennek a hosszú időskálájú változásnak a periódusát, amely
![]() napot tesz ki. A későbbi vizsgálatok nem erősítették meg egyértelműen
a másodlagos periódus létezését.
napot tesz ki. A későbbi vizsgálatok nem erősítették meg egyértelműen
a másodlagos periódus létezését.
Az 1950-es években kezdődött a csillag fotoelektromos vizsgálata. Masani és Broglia (1954) is megfigyelt a fénygörbéken a mérési hibánál nagyobb mértékű eltéréseket, nem ismétlődő sajátságokat. Hardie és Geilker (1958) készítették az első teljes fénygörbét UBV rendszerben.
1954-től a Konkoly Obszervatórium (ez az MTA CSKI angol szakirodalomban elterjedt
neve) is foglalkozott a csillaggal. Összegyűjtötték az 1980-ig fellelhető összes
maximumidőpontot és megalkották a DY Pegasi ![]() diagramját. Ennek eredményeként
két efemerist is közöltek. Egyik az
diagramját. Ennek eredményeként
két efemerist is közöltek. Egyik az ![]() diagram két egyenessel, másik a parabolával
való illesztéséből származó efemeris.
diagram két egyenessel, másik a parabolával
való illesztéséből származó efemeris.
A mérés
Méréseimet 2000 novembere és 2001 augusztusa között öt éjszakán át végeztem a Szegedi Csillagvizsgáló 40 cm-es és a Piszkéstetői Obszervatórium 90 cm-es műszereivel Johnson-féle V és B szűrővel. A képeket 30, 45, illetve 120 másodperces expozíciós idővel készítettem, attól függően, hogy melyik távcsövet használtam, és hogy milyen volt az ég minősége. A 18. táblázatban foglalom össze a mérési pontok számát.
Az apertúra fotometria segítségével elkészítettem az egyes éjszakák fénygörbéit, amelyhez a következő csillagokat használtam összehasonlítóként:
Összehasonlító csillag: GSC 1712-0984
Ellenőrző csillag: GSC 1712-0542
A 2001. augusztus 12/13. éjszaka fénygörbéje a 23. ábrán látható.
| dátum | pontok | obsz., műszer |
| 2001.01.01. | 101 | Pi 60, CCD B |
| 2001.08.03. | 166 | Sz 40, CCD V |
| 2001.08.04. | 152 | Sz 40, CCD V |
| 2001.08.12. | 253 | Sz 40, CCD V |
| 2001.08.15. | 339 | Sz 40, CCD V |
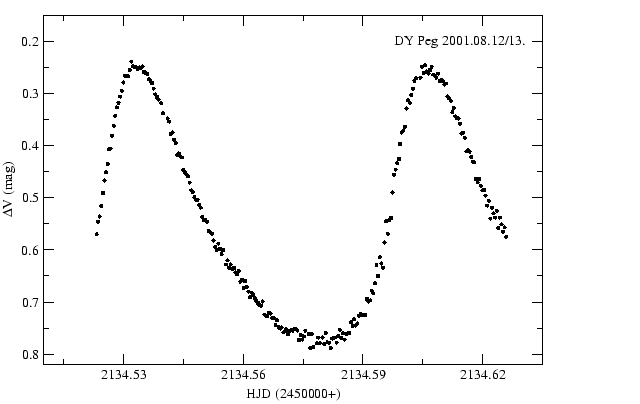
Az eredmények
A maximumidőpontok meghatározása (19. táblázat), valamint az irodalomban fellelhető
maximumidők összegyűjtése után elkészítettem az ![]() diagramját, amely a 24.
ábrán látható, amelyhez következő efemerist használtam (Hipparcos adatbázis):
diagramját, amely a 24.
ábrán látható, amelyhez következő efemerist használtam (Hipparcos adatbázis):
Az ![]() diagramra két illesztés végeztem: két egyenessel, valamint parabolával
próbáltam leírni a hosszútávú viselkedést. Gyakorlatilag nagyon kicsi az eltérés
a két illesztés között, a jelenlegi adatokból nem lehet eldönteni, hogy melyik
jellemzi helyesen a DY Pegasi periódusváltozását.
diagramra két illesztés végeztem: két egyenessel, valamint parabolával
próbáltam leírni a hosszútávú viselkedést. Gyakorlatilag nagyon kicsi az eltérés
a két illesztés között, a jelenlegi adatokból nem lehet eldönteni, hogy melyik
jellemzi helyesen a DY Pegasi periódusváltozását.
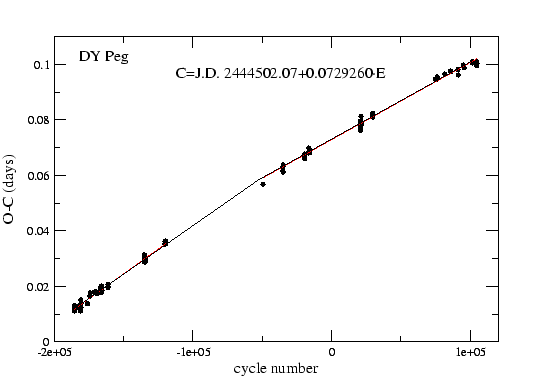
Az biztosan elmondható, hogy történt (történik) periódusváltozás, mert ha a
parabolás illesztést fogadjuk el, akkor folyamos csökkenést mutat a periódus,
ha pedig a két egyenessel való illesztést, akkor pedig egyszer történt egy periódusugrás.
Az egyenesek levonása után a 25. ábrán látható maradék ![]() diagramot kaptam.
diagramot kaptam.
| 1911,2338 | 0,1010 | 2134,5332 | 0,1010 |
| 1911,3062 | 0,1005 | 2134,6062 | 0,1010 |
| 2125,5619 | 0,0996 | 2137,5228 | 0,1006 |
| 2126,5833 | 0,1000 | 2137,5955 | 0,1004 |
Ebből arra lehet következtetni, hogy kb. HJD=2440600 körül egy hirtelen ugrás
történt a pulzációs periódusban. A levonás elvégzése után a maradék ![]() diagram
láthatóan az x tengellyel párhuzamos szakaszokból áll, azaz jó periódust mutat,
de a két szakasz között fázisbeli eltérés van, ami a hirtelen periódusváltozást
jelzi.
diagram
láthatóan az x tengellyel párhuzamos szakaszokból áll, azaz jó periódust mutat,
de a két szakasz között fázisbeli eltérés van, ami a hirtelen periódusváltozást
jelzi.
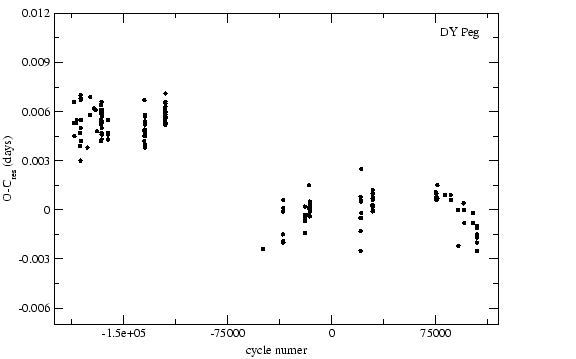
Az egyenessel, illetve a parabolával történt illesztést a következő formulák írják le:
1. Egyenesillesztés
2440600 előtt, E<![]() 52430:
52430:
2440600 után, E>![]() 52430:
52430:
2. Parabolaillesztés
Ha a hirtelen periódusugrás lehetőségét elfogadjuk, akkor ez szintén hasonló okokkal magyarázható, mint azt már az XX Cygni esetén említettem: eredhet a konvektív zóna anyagának szabálytalan áramlásaiból vagy a valamilyen nemlineáris pulzációs effektusból.
Ha folyamatos perióduscsökkenés történik, akkor azt a csillagfejlődés jeleként is értelmezhetjük.
Bevezetés
Hoffmeister fedezte fel 1935-ben, hogy változtatja fényességét és rövid periódusú változóként jellemezte. Még 1935-ben Soloviev sorolta be a csillagot W UMa-típusú változók közé, de nem sokkal késöbb megállapította a helyes típust. Ezen kívül vizuális megfigyelésiből meghatározott egy előzetes és hozzávetőleges periódusértéket, 0,14858 napot.
Fitch (1957) vette észre, hogy a fényességváltozás periódusa nem állandó. Ő volt az első, aki a periódust folytonosan változónak tekintette.
Spinrad (1959) fotoelektromos méréseiben azt találta, hogy a fénygörbék maximumának alakja változó ciklusról ciklusra, ennek ellenére azt jegyezte meg, hogy a fényváltozást meglehetősen állandónak találta. Később mások is vizsgálták az esetleges szabálytalanságokat a fényességváltozásban, de nem találtak erre vonatkozó egyértelmű bizonyítékokat.
A műszerek fejlődésével egyre nagyobb pontosságú méréseket végeztek, többek között Geyer és Hoffmann (1974), valamint Breger (1978). Ezek a mérések sem mutattak ki jelentős mértékű szabálytalanságokat a fénygörbén.
Szeidl és Mahdy (1981) a Konkoly Obszervatóriumban vizsgálták a csillagot. Összegyűjtötték
az akkori irodalomban fellelhető összes maximumidőpontot és elkészítették a
csillag ![]() diagramját, amelyből meghatározták, hogy a periódus folyamatos
csökkenést mutat.
diagramját, amelyből meghatározták, hogy a periódus folyamatos
csökkenést mutat.
Méréseim célja, hogy az irodalomban megtalálható maximumidőpontokat saját méréseimmel
kiegészítsem és elkészítve a csillag ![]() diagramját megvizsgáljam a periódus
jelenlegi értékét.
diagramját megvizsgáljam a periódus
jelenlegi értékét.
A mérés
2001 tavaszán öt éjszakán át végeztem méréseimet a Szegedi Csillagvizsgáló 40 cm-es távcsövével. A képeket V szűrőn keresztül készítettem 20 és 40 másodperc közötti expozíciós idővel az időjárási viszonyoknak megfelelően. A megfigyelések fő jellemzői a 20. táblázatban szerepelnek.
| dátum | pontok | obsz., műszer |
| 2001.05.09. | 509 | Sz 40, CCD V |
| 2001.05.10. | 663 | Sz 40, CCD V |
| 2001.05.19. | 409 | Sz 40, CCD V |
| 2001.06.25. | 506 | Sz 40, CCD V |
Az apertúra-fotometriához a következő összehasonlító csillagokat használtam:
Összehasonlító csillag: GSC 0968-1532
Ellenőrző csillag: GSC 0968-1002
A 2001. május 19/20. éjszaka fénygörbéje a 26. ábrán látható.
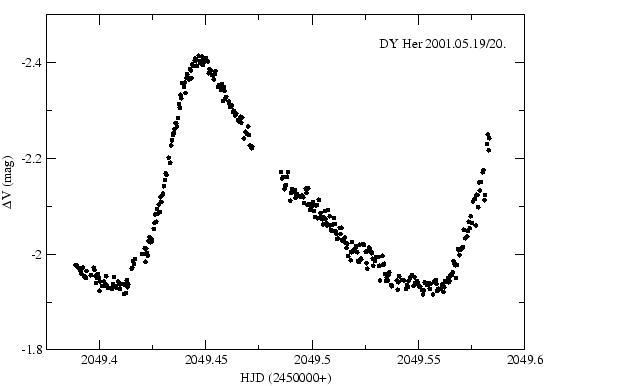
Az eredmények
Megszerkesztettem a csillag ![]() diagramját, amelyhez összegyűjtöttem az irodalomban
fellelhető összes maximumidőpontot, valamint meghatároztam a méréseimből származó
új időpontokat (21. táblázat). A számításnál a következő efemerist (epocha:
GCVS, periódus: Hipparcos adatbázis) használtam:
diagramját, amelyhez összegyűjtöttem az irodalomban
fellelhető összes maximumidőpontot, valamint meghatároztam a méréseimből származó
új időpontokat (21. táblázat). A számításnál a következő efemerist (epocha:
GCVS, periódus: Hipparcos adatbázis) használtam:
Az így kapott ![]() diagram a 27. ábrán látható.
diagram a 27. ábrán látható.
| 2040,3804 | 2049,4471 | ||
| 2040,5317 | 0,0010 | 2086,4579 | 0,0002 |
Az ![]() diagram alapján a pulzáció periódusa folyamatosan csökken. Ennek mértéke:
diagram alapján a pulzáció periódusa folyamatosan csökken. Ennek mértéke:
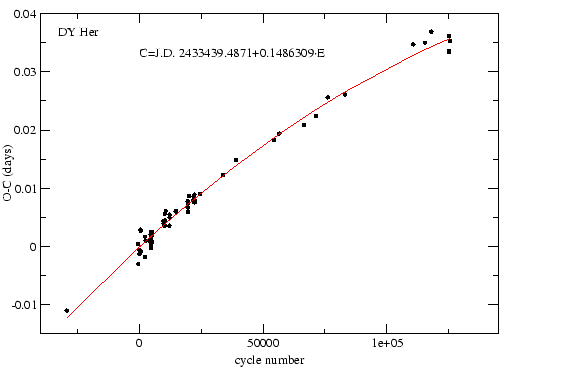
Az ![]() értékekből levonva az illesztett parabolát kaptam a 28. ábrán látható
maradvány
értékekből levonva az illesztett parabolát kaptam a 28. ábrán látható
maradvány ![]() diagramot. A pontok száma a mérési hiba nagyságrendjébe esik,
így a periódusváltozás leírása teljesnek tekinthető a kvadratikus illesztéssel.
Ebben az esetben is csillagfejlődési effektusnak tekinthetjük a megfigyelhető
periódusváltozást.
diagramot. A pontok száma a mérési hiba nagyságrendjébe esik,
így a periódusváltozás leírása teljesnek tekinthető a kvadratikus illesztéssel.
Ebben az esetben is csillagfejlődési effektusnak tekinthetjük a megfigyelhető
periódusváltozást.
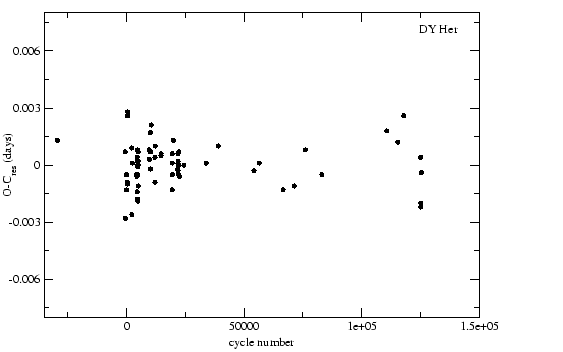
Bevezetés
Oja fedezte fel fényváltozását 1985 áprilisában. V szűrős amplitúdóját 0
![]() -nak,
periódusát 0,0958697 napnak határozta meg, valamint a következő efemerist adta
meg:
-nak,
periódusát 0,0958697 napnak határozta meg, valamint a következő efemerist adta
meg:
Rodríguez és munkatársai (1990) Strömgren rendszerben vizsgálták a csillagot.
Meghatározta az alapvető fizikai paramátereit és az ![]() diagram segítségével
pontosította a periódust. Azóta több mérést is végeztek periódusvizsgálat céljából.
Ezekből egymásnak ellentmondó eredmények születtek. Az
diagram segítségével
pontosította a periódust. Azóta több mérést is végeztek periódusvizsgálat céljából.
Ezekből egymásnak ellentmondó eredmények születtek. Az ![]() diagramhoz kezdetben
negatív parabolát (ami egyenletes perióduscsökkenést jelent), később pedig pozitívat
(ami egyenletes periódusnövekedést jelent) illesztettek. Méréseim célja, hogy
az
diagramhoz kezdetben
negatív parabolát (ami egyenletes perióduscsökkenést jelent), később pedig pozitívat
(ami egyenletes periódusnövekedést jelent) illesztettek. Méréseim célja, hogy
az ![]() diagramot újabb pontokkal egészítsem ki és megvizsgáljam a periódusváltozás
jelenlegi mértékét.
diagramot újabb pontokkal egészítsem ki és megvizsgáljam a periódusváltozás
jelenlegi mértékét.
A mérés
Méréseimet 2001-ben négy éjszakán át végeztem a Szegedi Csillagvizsgáló és a Piszkéstetői Obszervatórium műszereivel. A képeket Johnson-féle B és V szűrőkkel készítettem 8, 15 és 20 másodperces expozíciós idővel a használt távcső függvényében. Az egyes éjszakákon felvett pontok számát a 22. táblázat tartalmazza.
| dátum | pontok száma | obsz., műszer |
| 2001.02.24. | 215 | Pi 60, CCD B |
| 2001.02.24. | 830 | Pi 60, CCD V |
| 2001.03.14. | 224 | Sz 40, CCD V |
| 2001.03.16. | 438 | Sz 40, CCD V |
| 2001.12.08. | 193 | Sz 40, CCD V |
Az apertúra fotometriához a GSC 3425-0544 csillagot használtam összehasonlítóként. Sajnos a szegedi műszer kis látómezejébe nem fért be másik csillag, amit ellenőrzőnek lehetett volna használni.
Az eredmények
Szokásos módon a fénygörbékből (2001.02.24/25. fénygörbéje a 29. ábrán) alacsony fokszámú polinomot illesztve meghatároztam a kimért maximumok időpontjait (23. táblázat).
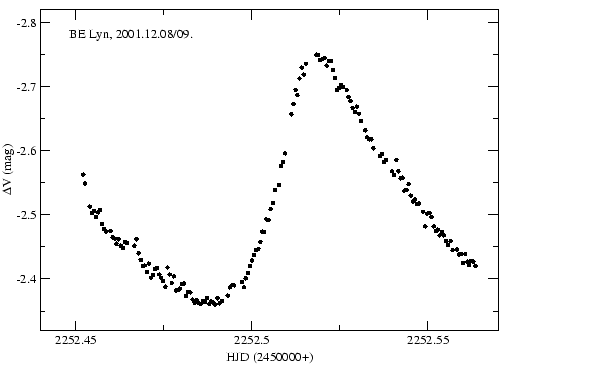
Az irodalomból kigyűjtött és általam meghatározott maximumidőpontok, valamint
a következő efemeris (Kiss és Szatmáry 1995) felhasználásával kiszámoltam az
![]() diagramot (30. ábra).
diagramot (30. ábra).
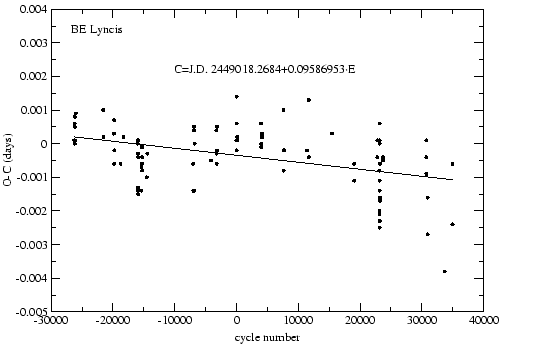
Ezt a 3.2 fejezetben tárgyalt fény-idő effektusra bemutatott képlet helyett
csak szinuszos függést feltételeztem az ![]() értékek mérési hibájához képest
igen kicsiny ingadozása és az ebből eredő bizonytalanság miatt:
értékek mérési hibájához képest
igen kicsiny ingadozása és az ebből eredő bizonytalanság miatt:
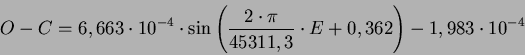
Ebből nagyságrendileg meg lehet becsülni a pálya vetületét, ha körpályát feltételezünk.
Ez az ![]() diagramra illesztett szinusz együtthatóinak egyenlővé tételével
a következő módon adódik:
diagramra illesztett szinusz együtthatóinak egyenlővé tételével
a következő módon adódik:
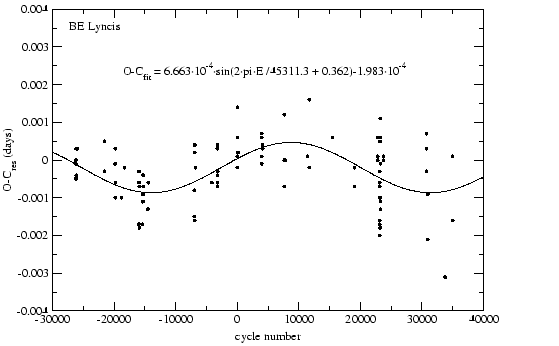
A 45311 ciklusnyi periódus ![]() 4300 nap orbitális periódust eredményez,
ami jelentősen hosszabb, mint amit Kiss és Szatmáry (1995) megadott. Sajnos
az új adatok továbbra is csak egy ciklusnyit ingadozó
4300 nap orbitális periódust eredményez,
ami jelentősen hosszabb, mint amit Kiss és Szatmáry (1995) megadott. Sajnos
az új adatok továbbra is csak egy ciklusnyit ingadozó ![]() diagramot adnak,
így a periodikus ingadozása, azaz a fény-idő effektus továbbra sem egyértelmű.
diagramot adnak,
így a periodikus ingadozása, azaz a fény-idő effektus továbbra sem egyértelmű.
További megfontolásokhoz vezet az ![]() diagram viszonylag nagy szórása, különösen
az utolsó öt évben. Hasonlóan a V567 Ophiuchi esetében, okozhatja több módus
egyidejű gerjesztettsége. Ennek vizsgálatára további méréseket tervezek.
diagram viszonylag nagy szórása, különösen
az utolsó öt évben. Hasonlóan a V567 Ophiuchi esetében, okozhatja több módus
egyidejű gerjesztettsége. Ennek vizsgálatára további méréseket tervezek.
| szűrő | ||
| 1965,2974 | V | |
| 1965,3927 | V | |
| 1965,4896 | B | 0,0001 |
| 1985,3329 | V | |
| 1985,5235 | V | |
| 2252,5183 | V |
Bevezetés
Fényességváltozását, amelyet 0,12 napos (2,8 óra) periódussal és 0
![]() 5-s amplitúdóval
végez, Cuno Hoffmeister fedezte fel 1949-ben. Az első fotografikus és vizuális
tanulmányozását Soloviev (1955) és Tsesevich (1956) végezték, akik W UMa-típusú
fedési kettősnek osztályozták és periódusát 0,274 napnak határozta meg. Schneller
(1961) és Eggen (1962) fotoelektromos méréseikkel elvetették ezt a besorolást
és RR jellegűnek mondták a változását. A helyes periódust Geffert és Szeidl
(1962), valamint Notni (1962) határozták meg, amelyet 0,12053 napnak találtak.
Geffert és Szeidl (1962) kis változásokat figyeltek meg a fénygörbe amplitúdójában.
Van Genderen (1967) is megfigyelte az amplitúdóbeli változásokat. Ő volt az
első, aki elkészítette az SZ Lyncis
5-s amplitúdóval
végez, Cuno Hoffmeister fedezte fel 1949-ben. Az első fotografikus és vizuális
tanulmányozását Soloviev (1955) és Tsesevich (1956) végezték, akik W UMa-típusú
fedési kettősnek osztályozták és periódusát 0,274 napnak határozta meg. Schneller
(1961) és Eggen (1962) fotoelektromos méréseikkel elvetették ezt a besorolást
és RR jellegűnek mondták a változását. A helyes periódust Geffert és Szeidl
(1962), valamint Notni (1962) határozták meg, amelyet 0,12053 napnak találtak.
Geffert és Szeidl (1962) kis változásokat figyeltek meg a fénygörbe amplitúdójában.
Van Genderen (1967) is megfigyelte az amplitúdóbeli változásokat. Ő volt az
első, aki elkészítette az SZ Lyncis ![]() diagramját és észrevette, hogy az
3,1 éves periódussal szinuszosan változik. Azután többen vizsgálták az amplitúdóváltozást,
de megoszlottak a vélemények a kérdésben. Barnes és Moffett (1975) pontosították
a periodikus változás paramétereit és a hosszú periódusú modulációt fény-idő
effektussal magyarázták. Garrido és munkatársai (1979) megerősítették ezt az
eredményt. A kettősség legerősebb bizonyítékai a radiálissebesség mérések voltak.
Woolley és Aly (1966) végeztek először radiálissebesség méréseket, majd McNamara
és Feltz (1976), de egyikük sem vett észre spektroszkópiai kettősséget. Bardin
és Imbert (1981) nagy időfelbontással végezte a radiálissebesség mérést. Az
eredmények egyértelműen megerősítették a kettőség hipotézisét. Legutoljára Paparó
és munkatársai (1988) és Moffett és munkatársai (1988) tanulmányozták a periódusváltozását.
Ezen cikkek óta nem végeztek újabb vizsgálatot az SZ Lyncisre.
diagramját és észrevette, hogy az
3,1 éves periódussal szinuszosan változik. Azután többen vizsgálták az amplitúdóváltozást,
de megoszlottak a vélemények a kérdésben. Barnes és Moffett (1975) pontosították
a periodikus változás paramétereit és a hosszú periódusú modulációt fény-idő
effektussal magyarázták. Garrido és munkatársai (1979) megerősítették ezt az
eredményt. A kettősség legerősebb bizonyítékai a radiálissebesség mérések voltak.
Woolley és Aly (1966) végeztek először radiálissebesség méréseket, majd McNamara
és Feltz (1976), de egyikük sem vett észre spektroszkópiai kettősséget. Bardin
és Imbert (1981) nagy időfelbontással végezte a radiálissebesség mérést. Az
eredmények egyértelműen megerősítették a kettőség hipotézisét. Legutoljára Paparó
és munkatársai (1988) és Moffett és munkatársai (1988) tanulmányozták a periódusváltozását.
Ezen cikkek óta nem végeztek újabb vizsgálatot az SZ Lyncisre.
A mérés
Méréseimet 2001 első felében végeztem két távcsővel. Két éjszakás mérés történt február végén a Piszkéstetői Obszervatórium 60 cm-es távcsövével, két éjszakás pedig a Szegedi Csillagvizsgáló 40 cm-es távcsövével. A képeket Johnson-féle V szűrőn keresztül készítettem 15 és 120 másodperces expozíciós idővel az ég minőségének megfelelően. A mérések jellemző adatai a 24. táblázatban találhatóak.
A CCD képek kiméréséhez két közeli összahasonlító csillagot válaszatottam:
Összehasonlító csillag: GSC 2979-1329
Ellenőrző csillag: GSC 2979-1343
| dátum | pontok | obsz., műszer |
| 2001.02.25. | 395 | Pi 60, CCD V |
| 2001.02.26. | 239 | Pi 60, CCD V |
| 2001.04.03. | 287 | Sz 40, CCD V |
| 2001.05.02. | 619 | Sz 40, CCD V |
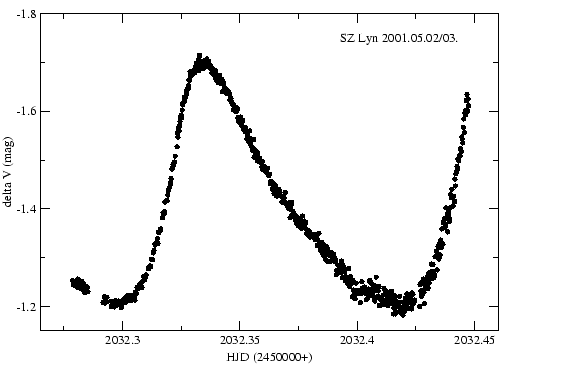
Az eredmények
A kapott fénygörbékre (a 2001.05.02. éjszaka fénygörbéje a 32. ábrán) kis fokszámú polinomot illesztve meghatároztam a maximumidőpontokat (25. táblázat). Négy új maximumot sikerült kimérni.
Az ![]() diagram elkészítéséhez kigyűjtöttem az irodalomban fellelhető összes
maximumidőpontot. A következő efemerist használtam a diagram kiszámításához
(epocha: GCVS, periódus: Hipparcos adatbázis):
diagram elkészítéséhez kigyűjtöttem az irodalomban fellelhető összes
maximumidőpontot. A következő efemerist használtam a diagram kiszámításához
(epocha: GCVS, periódus: Hipparcos adatbázis):
Az így kapott ![]() diagram a 33. ábrán látható.
diagram a 33. ábrán látható.
| 1966,5244 | 0,1233 | 2003,4072 | 0,1227 |
| 1967,3683 | 0,1234 | 2032,3351 | 0,1224 |
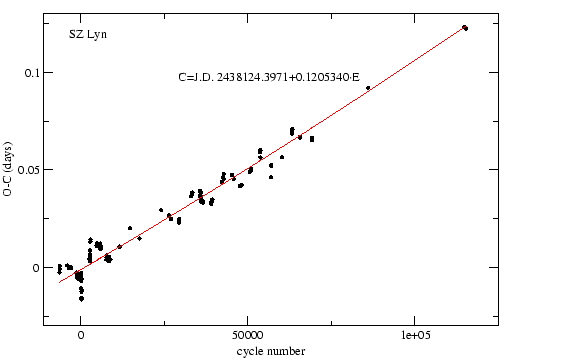
Az ![]() diagramra egy parabola illeszthető, amely azt jelzi, hogy a periódus
folyamatosan növekszik. A változás mértéke:
diagramra egy parabola illeszthető, amely azt jelzi, hogy a periódus
folyamatosan növekszik. A változás mértéke:
Ennek levonása után a 34. ábrán látható a maradvány ![]() diagram, amelyen hullámzás
figyelhető meg. Ez a már bevezetőben említett fény-idő effektus következménye.
Periódusának meghatározásához a Period98 program segítségével elkészítettem
az
diagram, amelyen hullámzás
figyelhető meg. Ez a már bevezetőben említett fény-idő effektus következménye.
Periódusának meghatározásához a Period98 program segítségével elkészítettem
az ![]() diagram Forurier-transzformáltját. Ennek eredményeként
diagram Forurier-transzformáltját. Ennek eredményeként ![]() napos periódust kaptam. Ez azt jelenti, hogy az SZ Lyncis egy kettős rendszer
tagja, amelynek keringési periódusa 1176,6 nap. A 35. ábrán látható ezzel a
periódussal fázisba rendezve a maradvány
napos periódust kaptam. Ez azt jelenti, hogy az SZ Lyncis egy kettős rendszer
tagja, amelynek keringési periódusa 1176,6 nap. A 35. ábrán látható ezzel a
periódussal fázisba rendezve a maradvány ![]() diagram.
diagram.
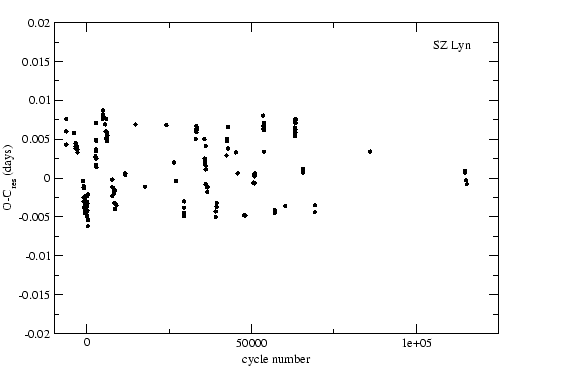
Az ![]() diagramra illesztett parabola másodrendű tagjának együtthatója,
diagramra illesztett parabola másodrendű tagjának együtthatója,
![]() .
Ez az érték nagyon jó egyezést mutat Szeidl (1983) cikkében megállapított
.
Ez az érték nagyon jó egyezést mutat Szeidl (1983) cikkében megállapított
![]() értékkel. Szintén jó az egyezés Moffett és munkatársai (1988) cikkében közölt
értékkel. Szintén jó az egyezés Moffett és munkatársai (1988) cikkében közölt
![]() értékkel. A keringési periódust
tekintve az
értékkel. A keringési periódust
tekintve az ![]() napos eredmény Paparó és munkatársai (1988) eredményeivel
vág össze legjobban, akik ugyanazt hozták ki. Moffett és munkatársai (1988)
napos eredmény Paparó és munkatársai (1988) eredményeivel
vág össze legjobban, akik ugyanazt hozták ki. Moffett és munkatársai (1988)
![]() nap orbitális periódust közöltek, amely kicsit hosszabb, de
ez a különbség sem számottevő.
nap orbitális periódust közöltek, amely kicsit hosszabb, de
ez a különbség sem számottevő.
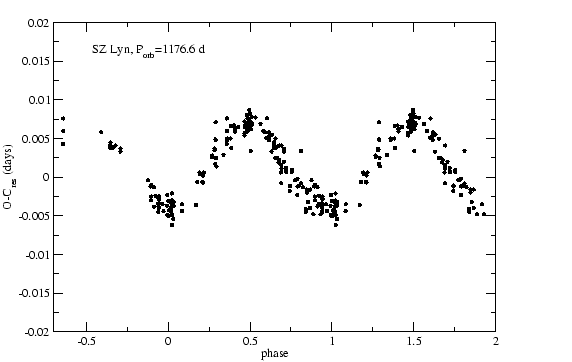
A nagyamplitúdójú ![]() Scuti-csillagok fotometriai felmérésének első eredményeit
poszteren bemutattuk a 2001 őszén megrendezett ``International Conference
on Variable Star Research'' nemzetközi konferencián (Brno, Csehország, Derekas
et al. 2002c). Az adatok feldolgozása, különös tekintettel a periódusváltozások
csillagfejlődési vonatkozásaira (Breger és Pamyatnikh 1998), jelenleg is folyamatban
van. A majdani eredmények várhatóan egy későbbi publikációban kerülnek bemutatásra.
Scuti-csillagok fotometriai felmérésének első eredményeit
poszteren bemutattuk a 2001 őszén megrendezett ``International Conference
on Variable Star Research'' nemzetközi konferencián (Brno, Csehország, Derekas
et al. 2002c). Az adatok feldolgozása, különös tekintettel a periódusváltozások
csillagfejlődési vonatkozásaira (Breger és Pamyatnikh 1998), jelenleg is folyamatban
van. A majdani eredmények várhatóan egy későbbi publikációban kerülnek bemutatásra.
Bevezetés
A V784 Cassiopeiae egy kisamplitúdójú (<0
![]() 4)
4) ![]() Scuti-típusú, több
módusban pulzáló változócsillag, melynek periódusa 0,1 nap (2,4 óra) nagyságrendű.
A Hipparcos asztrometriai műhold fedezte fel, az ebből származó paraméterei
az R00 katalógusban (Rodríguez és munkatársai 2000) találhatóak. 1983-ban Fernie
végzett UBVRI fotometriát az északi ég legérdekesebb Strömgren indexű csillagairól,
köztük a V784 Cassiopeiaeról. Az irodalomban található néhány radiális sebességmérés,
melyek eredményei elég széles tartományt ölelnek át,
Scuti-típusú, több
módusban pulzáló változócsillag, melynek periódusa 0,1 nap (2,4 óra) nagyságrendű.
A Hipparcos asztrometriai műhold fedezte fel, az ebből származó paraméterei
az R00 katalógusban (Rodríguez és munkatársai 2000) találhatóak. 1983-ban Fernie
végzett UBVRI fotometriát az északi ég legérdekesebb Strömgren indexű csillagairól,
köztük a V784 Cassiopeiaeról. Az irodalomban található néhány radiális sebességmérés,
melyek eredményei elég széles tartományt ölelnek át, ![]() 6 km s
6 km s![]() -tól (De
Medeiros és Mayor 1999) egészen 20 km s
-tól (De
Medeiros és Mayor 1999) egészen 20 km s![]() -ig (Duflot és munkatársai 1995).
Lèbre és De Medeiros (1997) vizsgálata nem talált semmilyen emmissziós jelleget
vagy aszimmetriát a H
-ig (Duflot és munkatársai 1995).
Lèbre és De Medeiros (1997) vizsgálata nem talált semmilyen emmissziós jelleget
vagy aszimmetriát a H![]() vonalprofiljában. Egyetlen tanulmány sem foglalkozik
az adatok időfüggésével, csak De Medeiros és Mayor (1999) sebességméréseinek
szórása (4 km s
vonalprofiljában. Egyetlen tanulmány sem foglalkozik
az adatok időfüggésével, csak De Medeiros és Mayor (1999) sebességméréseinek
szórása (4 km s![]() ) utalt lehetséges változásokra. Gray és munkatársai (2001)
határozták meg a spektráltípusát (F0-F2II), valamint a gyengén Am-típusú csillagok
közé sorolták.
) utalt lehetséges változásokra. Gray és munkatársai (2001)
határozták meg a spektráltípusát (F0-F2II), valamint a gyengén Am-típusú csillagok
közé sorolták.
Méréseim célja az volt, hogy meghatározzam a V784 Cassiopeiae pulzációs frekvenciáit és behatároljam a hozzájuk tartozó rezgési módusokat.
A mérés
2001. augusztus 29/30. és 2001. szeptember 9/10. között, 12 éjszakán át végeztem méréseket Spanyolországban, a Sierra Nevadai Obszervatórium 0,9m-es Ritchey-Chrétien-típusú távcsövének és négycsatornás spektrofotométerének segítségével.
A 12 éjszaka alatt összesen 58,4 órán át mértem a csillagot. Mivel más célú mérések is történtek, ezért az időjárás hatásain kívül ezek hossza is befolyásolta az egyes éjszakákon végzett mérések időtartamát. A mérések éjszakákra való leosztását a 26. táblázat foglalja össze.
A mérésekhez differenciális fotometriai módszer használtam, mert közeli csillagok fényességkülönbségében a légkör extinkciója elhanyagolható. Ehhez a következő összehasonlító (comp) ill. ellenőrző (check) csillagokat használtam:
| dátum | pontok száma | dátum | pontok száma |
| 2001.08.29. | 166 | 2001.09.04. | 177 |
| 2001.08.30. | 234 | 2001.09.05. | 210 |
| 2001.08.31. | 178 | 2001.09.06. | 228 |
| 2001.09.01. | 251 | 2001.09.07. | 84 |
| 2001.09.02. | 93 | 2001.09.08. | 257 |
| 2001.09.03. | 206 | 2001.09.09. | 279 |
A három csillag égi elhelyezkedését a következő képen mutatom be:

Ezen összehasonlítók esetében gyakorlatilag semmilyen fényesség vagy színváltozás
nem figyelhető meg, ami nagyobb lenne ![]() 0
0![]() 005-nál.
005-nál.
A mérések olyan ciklusban zajlottak, hogy egyszer az összehasonlítót (comp), majd az ellenőrzőt (check), ezután pedig háromszor a változót, végül az égi hátteret mértem.
A 12 éjszaka együttes fénygörbéje a Strömgren-féle ![]() fényességben
a 37. ábrán látható. A fénygörbén sejthető a lebegés jelensége, így már ``ránézésre''
azt sugallja, hogy az éjszakáról éjszakára változó alakú fénygörbék frekvencia-analízise
egymáshoz közeli frekvenciákat (is) kiad.
fényességben
a 37. ábrán látható. A fénygörbén sejthető a lebegés jelensége, így már ``ránézésre''
azt sugallja, hogy az éjszakáról éjszakára változó alakú fénygörbék frekvencia-analízise
egymáshoz közeli frekvenciákat (is) kiad.
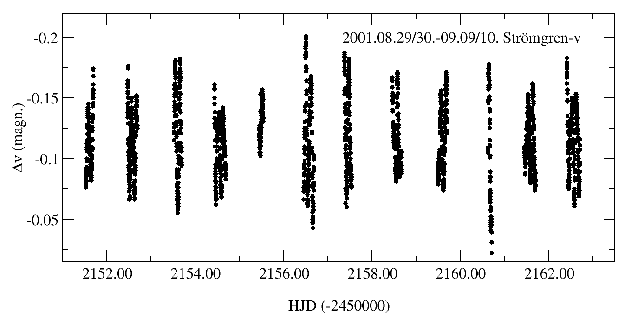
Frekvencia-analízis
Mielőtt a frekvencia-analízist elvégeztem volna, áttranszformáltam a fényességértékeket standard V magnitúdókká.
A frekvencia-analízist a standard Fourier-transzformáció módszerével végeztem
egymást követő fehérítési lépések segítségével, amelyhez a Period98 (Sperl 1998)
nevű programot használtam. Ez a program a paraméterek sokfrekvenciás, legkisebb
négyzetes illesztésének módszerét alkalmazza. A méréseket a 0-50 ciklus/napos
frekvenciatartományban vizsgáltam
![]() -es lépésközzel.
-es lépésközzel.
A 38. ábra a fehérítés egyes lépései során kapott Fourier-spektrumokat mutatja.
Az elsődleges csúcs az ![]() =9,154038 ciklus/nap-nél található, amplitúdója
39,7 mmag. Az eljárást akkor fejeztem be, amikor a Fourier-spektrum zajjá csökkent,
amely 0
=9,154038 ciklus/nap-nél található, amplitúdója
39,7 mmag. Az eljárást akkor fejeztem be, amikor a Fourier-spektrum zajjá csökkent,
amely 0
![]() 003-nál következett be. A kapott frekvenciákat a 27. táblázat foglalja
össze.
003-nál következett be. A kapott frekvenciákat a 27. táblázat foglalja
össze.
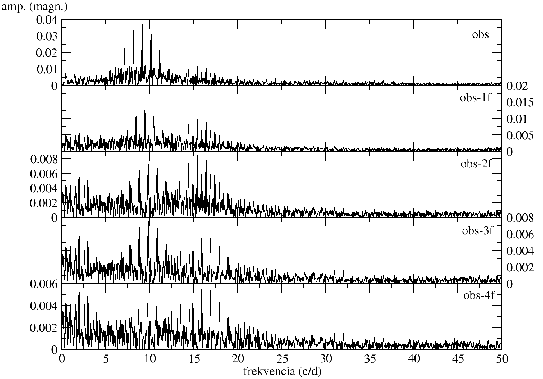
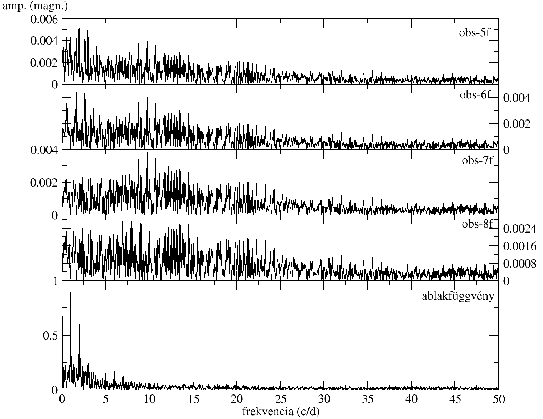
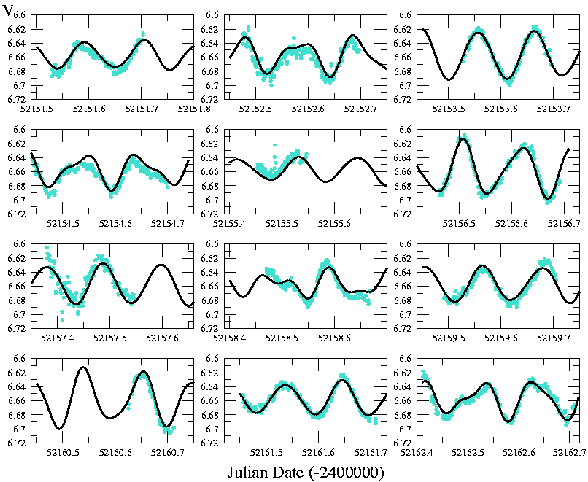
| P (nap) | A (mmag.) |
|
||
| F |
9,154038 | 0,109241 | 39,7 | 0,0162 |
| F |
9,463398 | 0,105670 | 13,9 | 0,7967 |
| F |
15,406044 | 0,06491 | 8,9 | 0,4801 |
| F |
9,86088 | 0,101411 | 7,9 | 0,9211 |
| F |
15,915408 | 0,062832 | 5,4 | 0,9922 |
| F |
1,995573 | 0,501109 | 7,1 | 0,5165 |
| F |
1,638695 | 0,610242 | 4,2 | 0,6037 |
| F |
9,778661 | 0,102263 | 4,9 | 0,7168 |
Az ablakfüggvényben az 1 ciklus/nap frekvenciaközzel jelenik meg erős csúcs, ami a 12 napon át tartó minden napos mérés miatt jelentkezik.
A periódus-analízissel kapott frekvenciákból adódó összegszinusz 12 éjszakán mért pontokra való illeszkedését a 39. ábrán mutatom be.
Az adatok értelmezése
Ha figyelmesen végignézzük a kapott frekvenciákat, észrevehetjük, hogy három
fő frekvencia köré csoportosulnak az értékek. Egyik csoport a 9 és 10 ciklus/nap
közé, egy másik csoport a 15 és 16 ciklus/nap közé, míg a harmadik csoport egy
kis frekvenciás, 1,5 és 2 ciklus/nap közé esik. Ha kiszámítjuk az ![]() és
és ![]() frekvenciák
arányát, akkor 0,59-et kapunk. Ez azért fontos, mert az elméleti számolások
szerint 0,6 a radiális alapmódus és a második felhang aránya. Ebből egy lehetséges
következtetés, hogy az
frekvenciák
arányát, akkor 0,59-et kapunk. Ez azért fontos, mert az elméleti számolások
szerint 0,6 a radiális alapmódus és a második felhang aránya. Ebből egy lehetséges
következtetés, hogy az ![]() frekvenciájú rezgés az alapmódusú pulzációnak,
az
frekvenciájú rezgés az alapmódusú pulzációnak,
az ![]() pedig a második felhangjának fogható fel. Ebben az esetben az
pedig a második felhangjának fogható fel. Ebben az esetben az ![]() =
9,154038 ciklus/nap frekvencia radiális pulzációként értelmezhető. Ha ezt így
fogadjuk el, akkor ebből az következik, hogy az
=
9,154038 ciklus/nap frekvencia radiális pulzációként értelmezhető. Ha ezt így
fogadjuk el, akkor ebből az következik, hogy az ![]() = 15,406044 ciklus/nap
frekvencia is radiális, méghozzá
= 15,406044 ciklus/nap
frekvencia is radiális, méghozzá ![]() második felhangja.
második felhangja.
A harmadik csoportba sorolt frekvenciákkal (1,5 és 2 ciklus/nap közé esők) kapcsolatban úgy tűnik, hogy feltehetően az összehasonlító csillag piciny ingadozásai hozták be, ugyanis a két összehasonlító csillag fényességkülönbsége sajnos néhány ezredmagnitúdónyit változott éjszakáról éjszakára.
Mindezek alapján azt a következtetést lehet levonni, hogy a V784 Cassiopiae pulzációjában hat frekvenciát sikerült egyértelműen kimutatni.
Szót kell még ejteni az egyes perióduscsoportok jelentéséről. Ha ![]() és
és ![]() radiális
módusok, akkor az
radiális
módusok, akkor az ![]() ,
, ![]() ,
, ![]() illetve az
illetve az ![]() frekvenciájú rezgés ezek
nem radiális módusai lehetnek.
frekvenciájú rezgés ezek
nem radiális módusai lehetnek.
Az itt bemutatott V784 Cassiopeiae mérések egy jóval bővebb fotometriai és spektroszkópiai analízisbe épültek be, melyek eredményeit az Astronomy & Astrophysics folyóirathoz küldtük be megjelenésre (Kiss és munkatársai 2002).
Dolgozatomban a 2000. augusztus és 2002. január között, összesen kb. 70 éjszakán végzett csillagászati megfigyeléseimet és a belőlük levont következtetéseimet mutattam be. Az eredményeket röviden a következőképpen foglalhatjuk össze:
A dolgozatban részletezett eredmények egy részét már publikáltuk (l. Függelék),
ám a legérdekesebb vizsgálatok még jelenleg is zajlanak a nagyamplitúdójú ![]() Scuti-csillagok témájában. A továbbiakban lehetőségeimhez mérten ezeket a kutatásokat
szeretném folytatni, részben új többszín-fotometriai és spektroszkópiai mérések
felvételével, részben az elméleti háttér részletesebb megismerésével és az eddigi
eredmények mélyebb beágyazásával.
Scuti-csillagok témájában. A továbbiakban lehetőségeimhez mérten ezeket a kutatásokat
szeretném folytatni, részben új többszín-fotometriai és spektroszkópiai mérések
felvételével, részben az elméleti háttér részletesebb megismerésével és az eddigi
eredmények mélyebb beágyazásával.
Ezúton szeretném megköszönni témavezetőmnek, Dr. Kiss Lászlónak, az elmúlt években nyújtott folyamatos segítségét és útmutató tanácsait. Hasonlóan köszönettel tartozom tanáraimnak, Dr. Szatmáry Károlynak és Dr. Vinkó Józsefnek, tanulmányaimban nyújtott önzetlen segítségükért, tanácsikért, valamint a külföldi mérésekben, illetve a konferencián való részvételemhez nyújtott támogatásukért. Bő másfél éves munkám során több hallgatótársamtól kaptam nélkülözhetetlen technikai, megfigyelési, vagy csak egyszerűen baráti segítséget, amiért köszönettel tartozom. Ők a következők (alfabetikus sorrendben): Bebesi Zsófia, Csák Balázs, Fűrész Gábor, Heiner Zsuzsa, Mészáros Szabolcs, Sárneczky Krisztián, Szabó Gyula, Székely Péter, Váradi Mihály. Kutatásaimat a következő pályázatok támogatták: OTKA T03225, T034615, OM FKFP 0010/2001. Végül, de nem utolsó sorban, köszönetet mondok szüleimnek tanulmányaim során nyújtott szerető támogatásukért.
A dolgozatomban bemutatott eredményekhez kötődő publikációk a következők:
Ezek másolatait gyűjtöttem össze jelen Függelékbe.
This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.42)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_subdir -split 0 -show_section_numbers /home/aliz/tdk/tdk.tex
The translation was initiated by on 2002-06-25