Vizsgáljuk meg a tömegpontnak tekintett csillagok mozgását a Tejútrendszer
tengelyszimmetrikus gravitációs terében!
Egy tetszőleges m tömegű csillag mozgásegyenlete:
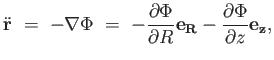 |
(4.16) |
ahol r a csillag helyvektora a középponttól mint origótól számítva,
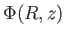 a gravitációs potenciál.
A helyvektor időderiváltjának hengerkoordináta-rendszerben
kifejezett alakját felhasználva a mozgásegyenlet három komponense így alakul:
a gravitációs potenciál.
A helyvektor időderiváltjának hengerkoordináta-rendszerben
kifejezett alakját felhasználva a mozgásegyenlet három komponense így alakul:
(4.19) első integrálja
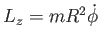 , a z-irányú impulzusmomentum.
Legyen
, a z-irányú impulzusmomentum.
Legyen
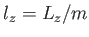 , a tömegegységre vonatkozó impulzusmomentum. Ezzel (4.19)
a következő alakot ölti:
, a tömegegységre vonatkozó impulzusmomentum. Ezzel (4.19)
a következő alakot ölti:
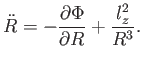 |
(4.20) |
Vezessük be az effektív potenciált a következő definícióval:
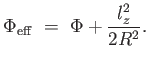 |
(4.21) |
A 4.19 egyenlet így a következő formába írható át:
Az effektív potenciálnak minimuma van a z=0 fősíkban lévő körpályán történő
keringés esetén. Valóban, a
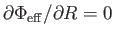 egyenlet megoldásából
egyenlet megoldásából
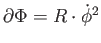 adódik, ami a körmozgás egyenlete (
adódik, ami a körmozgás egyenlete (
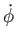 a szögsebesség).
a szögsebesség).
Jelöljük a körpálya sugarát 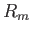 -mel, és fejtsük Taylor-sorba
-mel, és fejtsük Taylor-sorba
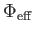 -t
minimumhelye (azaz
-t
minimumhelye (azaz 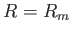 és z=0) körül:
és z=0) körül:
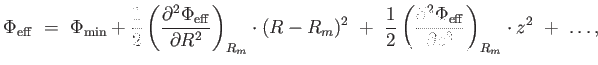 |
(4.24) |
mert az elsőrendű deriváltak a minimumhelyen 0-t adnak, a másodrendű vegyes derivált pedig
a függvény alakja miatt esik ki. Az effektív potenciál tehát a másodrendű tagokig
bezárólag a következő alakba írható:
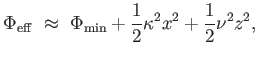 |
(4.25) |
ahol
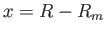 , a másodrendű deriváltakat pedig
, a másodrendű deriváltakat pedig
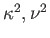 -tel jelöltük.
Ezzel a (4.23) mozgásegyenletek a következő alakot öltik:
-tel jelöltük.
Ezzel a (4.23) mozgásegyenletek a következő alakot öltik:
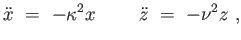 |
(4.26) |
ami a harmonikus rezgőmozgás egyenlete x-re és z-re is. Tehát
a csillag mozgása két egymásra merőleges irányú harmonikus rezgés szuperpozíciójából
áll elő.
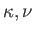 szokásos elnevezése: epiciklus frekvencia.
(4.26) megoldásai:
szokásos elnevezése: epiciklus frekvencia.
(4.26) megoldásai:
Látható, hogy a csillag keringése során mind a pálya központtól mért R
sugara, mind a fősíktól való z távolsága oszcillál. A kétféle oszcilláció közti
fáziskülönbséget jelöli 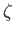 .
.
A keringés szögsebessége a definíció alapján:
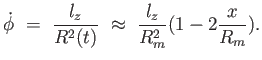 |
(4.29) |
ahol kihasználtuk, hogy 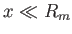 . A fenti egyenlet integrálásával kaphatjuk a csillag
időfüggő szögkoordinátáját:
. A fenti egyenlet integrálásával kaphatjuk a csillag
időfüggő szögkoordinátáját:
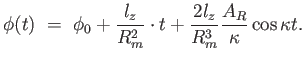 |
(4.30) |
Ha
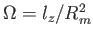 a körpályán való keringés körfrekvenciája, adódik:
a körpályán való keringés körfrekvenciája, adódik:
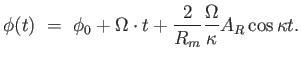 |
(4.31) |
Látható, hogy a szögkoordináta nem egyenletesen változik, mint tiszta körmozgás esetén,
hanem a szögsebesség az epiciklus frekvenciával oszcillál az egyenletes körmozgás
szögsebessége körül. A csillag tehát időnként ``siet'', időnként ``késik'' a körpályán történő
mozgáshoz képest.
Az epiciklus frekvencia egyszerűen kifejezhető a fentebb definiált Oort-konstansokkal.
A definíciók felhasználásával adódik, hogy
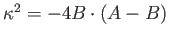 . A Napra
. A Napra
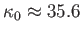 km/s/kpc. Mivel az LSR szögsebessége
km/s/kpc. Mivel az LSR szögsebessége
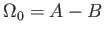 ,
a kettő aránya:
,
a kettő aránya:
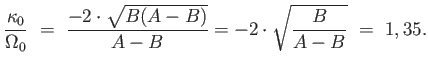 |
(4.32) |
Mivel a kétféle körfrekvencia aránya nem egész szám, a pálya egy keringés során nem lesz
zárt görbe.
Szeged
2013-05-01
![]() , a z-irányú impulzusmomentum.
Legyen
, a z-irányú impulzusmomentum.
Legyen
![]() , a tömegegységre vonatkozó impulzusmomentum. Ezzel (4.19)
a következő alakot ölti:
, a tömegegységre vonatkozó impulzusmomentum. Ezzel (4.19)
a következő alakot ölti:
![]() egyenlet megoldásából
egyenlet megoldásából
![]() adódik, ami a körmozgás egyenlete (
adódik, ami a körmozgás egyenlete (
![]() a szögsebesség).
a szögsebesség).
![]() -mel, és fejtsük Taylor-sorba
-mel, és fejtsük Taylor-sorba
![]() -t
minimumhelye (azaz
-t
minimumhelye (azaz ![]() és z=0) körül:
és z=0) körül:
![]() . A Napra
. A Napra
![]() km/s/kpc. Mivel az LSR szögsebessége
km/s/kpc. Mivel az LSR szögsebessége
![]() ,
a kettő aránya:
,
a kettő aránya: