Gömbszimmetria esetén a gravitációt jellemző metrikus tenzor (és a belőle
alkotott
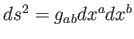 ívelem-négyzet) mindössze két szabad függvényt tartalmaz:
ívelem-négyzet) mindössze két szabad függvényt tartalmaz:
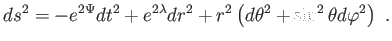 |
(5.4) |
A gömbszimmetria miatt a
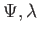 függvények nem függenek a
függvények nem függenek a
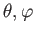 szögváltozóktól. Mivel egyensúlyi helyzetet vizsgálunk, a függvényeknek explicit időfüggésük sem lesz, azaz csupán az
szögváltozóktól. Mivel egyensúlyi helyzetet vizsgálunk, a függvényeknek explicit időfüggésük sem lesz, azaz csupán az 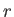 radiális koordináta függvényei. A metrika
radiális koordináta függvényei. A metrika 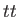 komponense
komponense
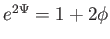 módon is írható, gyenge tér közelítésben az új
módon is írható, gyenge tér közelítésben az új 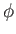 metrikus függvény éppen a newtoni
gravitációs potenciál. Ennek az összefüggésnek a deriváltjából
metrikus függvény éppen a newtoni
gravitációs potenciál. Ennek az összefüggésnek a deriváltjából
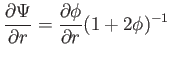 |
(5.5) |
következik. A 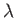 metrikus függvény helyett pedig bevezethetjük az
metrikus függvény helyett pedig bevezethetjük az 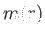 tömegfüggvényt
tömegfüggvényt
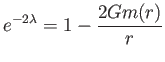 |
(5.6) |
összefüggéssel.
Subsections
Szeged
2013-05-01
![]() ívelem-négyzet) mindössze két szabad függvényt tartalmaz:
ívelem-négyzet) mindössze két szabad függvényt tartalmaz: