Next: Az Oppenheimer-Volkoff-egyenlet Up: Gömbszimmetrikus csillagok hidrosztatikai egyensúlya Previous: Gömbszimmetrikus csillagok hidrosztatikai egyensúlya
Barotropikus ideális folyadékot feltételezve, az Einstein-egyenletek rendkívüli módon egyszerűsödnek: csupán 3 diagonális egyenlet marad. A ![]() és az
és az ![]() egyenletek explicit alakja
egyenletek explicit alakja
Newtoni határesetben
![]() és a nyomás elhanyagolható a sűrűség
mellett. Így az (5.5) és az (5.9) egyenletekből a
hidrosztatikai egyensúly
és a nyomás elhanyagolható a sűrűség
mellett. Így az (5.5) és az (5.9) egyenletekből a
hidrosztatikai egyensúly
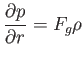 |
(5.10) |
Szeged 2013-05-01