Next: A belső Schwarzschild-megoldás Up: Gömbszimmetrikus csillagok hidrosztatikai egyensúlya Previous: Barotropikus csillag téregyenletei
Az (5.7) egyenlet átírható
![$\displaystyle \frac{d}{dr}\left[ r\left( 1-e^{-2\lambda }\right) \right] =8\pi Gr^{2}\rho$](img882.png) |
(5.11) |
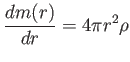 |
(5.12) |
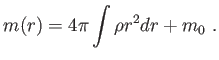 |
(5.13) |
Az (5.8) és (5.6) egyenletekből a következőt kapjuk:
Pozitív nyomású anyag mellett az (5.15) egyenlet jobb oldalán mindkét számlálóbeli szorzó nagyobb, míg a nevező kisebb a newtoni (5.16) egyenletben található megfelelő tagoknál, vagyis az általános relativisztikus esetben a nyomás növekedése az origóhoz (csillag belsejéhez) közeledve hangsúlyosabb a newtoninál. Az eltérés a csillag kompaktságának mértékével együtt nő.5.4 Kompakt égitesteknél (fehér törpék, neutroncsillagok) az eltérések jelentősek.
Szeged 2013-05-01