Next: Gömbszimmetrikus fekete lyukak Up: Gravitációs kollapszus és fekete Previous: Gravitációs kollapszus és fekete
Az egyszerűség kedvéért modellezzük az összehúzódó csillag anyagát nyomásmentes ideális folyadékkal (porral) és tekintsük gömbszimmetrikusnak. Az ívelemnégyzet egy Friedmann-Lemaître-Robertson-Walker-téridő (FLRW), amely
együttmozgó
![]() koordinátákban:
koordinátákban:
| (5.29) |
A csillag határa konstans együttmozgó
![]() koordinátánál található, ennek külső tartományában az (5.25) külső Schwarzschild-téridő érvényes. A
koordinátánál található, ennek külső tartományában az (5.25) külső Schwarzschild-téridő érvényes. A
![]() koordinátahármas az
illesztési felület koordinátáinak választható. A két tartománynak a közös felületen indukált metrikái
koordinátahármas az
illesztési felület koordinátáinak választható. A két tartománynak a közös felületen indukált metrikái
![$\displaystyle \left[ -\left( 1-\frac{2GM}{r_{0}}\right) \dot{t}%
_{0}^{2}+\left( 1-\frac{2GM}{r_{0}}\right) ^{-1}\dot{r}_{0}^{2}\right] d\tau
^{2}$](img953.png) |
|||
| (5.32) | |||
| (5.33) |
Az illesztési felület külső görbületének a csillag felőli oldalról nézve
csak két nemeltűnő komponense van, ezek
![]() . A belső, illetve a külső tartományból látszó megfelelő külső görbületkomponensek:
. A belső, illetve a külső tartományból látszó megfelelő külső görbületkomponensek:
| (5.36) | |||
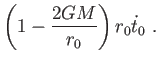 |
(5.37) |
Az (5.39) összefüggés integrálása megadja az összeomló csillag skálafaktorának időfejlődését a ![]() együttmozgó idő függvényében:
együttmozgó idő függvényében:
A (5.30) fejlődésegyenlet segítségével a központi tömeg kifejezhető az
energiasűrűség és a csillag sugara segítségével. Eszerint ![]() a csillag
energiasűrűségének térfogati integrálja
a csillag
energiasűrűségének térfogati integrálja
Összefoglalva, a kollapszus végtelen sűrűségű ponttá húzza össze a csillagot, mégpedig véges idő elteltével. A pont tehát egy szingularitás, amelynek külső környezete a Schwarzschild-téridő lesz.
Szeged 2013-05-01