Illesztés külső vákuummal

A gravitációt jellemző metrika az $a,b,r_{1}$ paraméterek függvénye, ezek közül az (5.20) összefüggések segítségével csupán kettő küszöbölhető ki a csillag

fizikai paraméterei segítségével. A harmadik paraméter nem csupán a csillagtól, hanem annak környezetétől is függ. Amennyiben a csillag külseje gömbszimmetrikus vákuum ( $T_{ab}=0$ ), Birkhoff unicitás-tételének értelmében ez a

$\displaystyle ds_{S_{k\ddot{u}lso}}^{2}=-\left( 1-\frac{2GM}{r}\right) dt^{2}+\... ...ight) ^{-1}dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right)$

(5.25)

Két téridő illesztésénél az ún. Israel-féle illesztési feltételeknek kell teljesülniük. Mint ahogyan az elektromágneses mennyiségek összes komponensének sem kell a töltéseket és áramokat tartalmazó határátmeneten folytonosnak lennie, a metrikus tenzor összes komponensére sem követeljük ezt meg. A gravitációs illesztési feltételek értelmében az illesztési felület indukált metrikája (első fundamentális formája) mindig folytonos, míg a külső görbülete (második fundamentális formája) csak akkor, ha a felszínen nincs disztribucionális anyag.

A $g_{tt}$ metrikus függvény folytonossága az

felület indukált metrikájának folytonosságából következik, és az

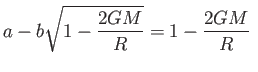$\displaystyle a-b\sqrt{1-\frac{2GM}{R}}=1-\frac{2GM}{R}$

(5.26)

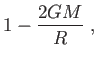$\displaystyle \frac{2a}{3}$	$\displaystyle =$	$\displaystyle 1-\frac{2GM}{R} ,$
$\displaystyle 2b$	$\displaystyle =$	$\displaystyle \sqrt{1-\frac{2GM}{R}}$	(5.27)

Összefoglalva, a belső Schwarzschild-megoldás és ennek tömegfüggvénye abban az esetben, ha a csillagot vákuum veszi körül:

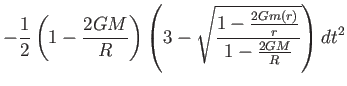$\displaystyle ds_{S_{belso}}^{2}$	$\displaystyle =$	$\displaystyle -\frac{1}{2}\left( 1-\frac{2GM}{R}\right) \left( 3- \sqrt{\frac{1-\frac{2Gm(r)}{r}}{1-\frac{2GM}{R}}}\right) dt^{2}$
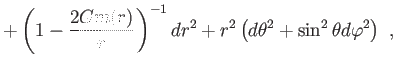		$\displaystyle +\left( 1-\frac{2Gm(r)}{r}\right) ^{-1}dr^{2}+r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) ,$
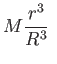$\displaystyle m(r)$	$\displaystyle =$	$\displaystyle M\frac{r^{3}}{R^{3}}$	(5.28)