Next: Energiafeltételek Up: Gravitációs kollapszus és fekete Previous: Oppenheimer-Snyder-kollapszus
Az (5.25) Schwarzschild-téridőről könnyen belátható, hogy a metrikus
tenzor komponensei divergálnak ![]() és
és ![]() helyeken. Meg lehet mutatni,
hogy előbbi egy igazi szingularitás (az
helyeken. Meg lehet mutatni,
hogy előbbi egy igazi szingularitás (az ![]() görbületi skalár is divergens),
utóbbi azonban csak a rossz koordinátaválasztás következménye. Valóban, léteznek olyan koordináták, amelyekben a metrika jól viselkedik az
görbületi skalár is divergens),
utóbbi azonban csak a rossz koordinátaválasztás következménye. Valóban, léteznek olyan koordináták, amelyekben a metrika jól viselkedik az ![]() helyen. Ilyenek az Eddington-Finkelstein- és a Kruskal-Szekeres-koordináták. Mindkettőhöz null (fényszerű) koordináták bevezetése szükséges:
helyen. Ilyenek az Eddington-Finkelstein- és a Kruskal-Szekeres-koordináták. Mindkettőhöz null (fényszerű) koordináták bevezetése szükséges:
| (5.44) |
| (5.45) |
Felhasználva, hogy
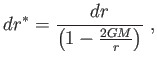 |
(5.46) |
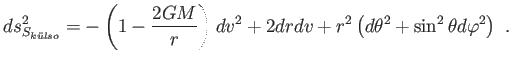 |
(5.47) |
Végezetül megjegyezzük, hogy az általános relativitáselmélet első kísérleti bizonyítékai a Schwarzschild-téridőhöz kapcsolódnak. A Naprendszert (a Nap belsejének kivételével) Schwarzschild-téridővel modellezve, a tömeges és tömeg nélküli részecskepályák vizsgálatából a keringő bolygók perihélium-elfordulását és a Nap mellett elhaladó fény elhajlását kapjuk. A megfigyelések nagy pontossággal erősítették meg az elmélet jóslatait.
Szeged 2013-05-01