Elsődleges nukleoszintézis

Amikor az Univerzum a deuteronok kötési energiájának megfelelő hőmérséklet alá hűl, stabil deuteron-atommagok alakulnak ki. (A kötési energiák nagyságrendjébe eső hőmérsékleteken kialakuló atommagokat a magas energiájú fotonok még lerombolják.) Az alacsony [12]

$\displaystyle \eta _{b}\sim 10^{-9}$

(6.65)

barion/foton arány miatt csak $T\approx 8,1\times 10^{8}$ K (

MeV) hőmérsékleten indul be a deuteronok ( $^{2}H$ ) szintézise. Mivel az egy barionra eső kötési energia a vasatommag esetén a legkisebb, energetikailag ennek a kialakulása lenne a legkedvezőbb, azonban az Univerzum folyamatos lehűlése ezt megakadályozza.

A deuteronok létrejöttével megindul a triton- és a héliumatommagok képződése a

$\displaystyle ^{2}$ H $\displaystyle +n$	$\displaystyle \rightarrow$	$\displaystyle ^{3}$ H $\displaystyle +\gamma , ^{3}$ H $\displaystyle +p\rightarrow ^{4}$ He $\displaystyle +\gamma ,$
$\displaystyle ^{2}$ H $\displaystyle +p$	$\displaystyle \rightarrow$	$\displaystyle ^{3}$ He $\displaystyle +\gamma , ^{3}$ He $\displaystyle +n\rightarrow ^{4}$ He $\displaystyle +\gamma$	(6.66)

fotoemisszióval járó és a

$\displaystyle ^{2}$ H $\displaystyle + ^{2}$ H	$\displaystyle \rightarrow$	$\displaystyle ^{3}$ He $\displaystyle +n , ^{2}$ H $\displaystyle + ^{2}$ H $\displaystyle \rightarrow ^{3}$ H $\displaystyle +p ,$
$\displaystyle ^{3}$ H $\displaystyle + ^{2}$ H	$\displaystyle \rightarrow$	$\displaystyle ^{4}$ He $\displaystyle +n , ^{3}$ He $\displaystyle + ^{2}$ H $\displaystyle \rightarrow ^{4}$ He $\displaystyle +p ,$	(6.67)

fotoemisszió-mentes folyamatokon keresztül. A $T\approx 5,8\times 10^{8}$ K hőmérsékletnél (

MeV) a

$\displaystyle ^{2}$ H $\displaystyle + ^{2}$ H $\displaystyle \rightarrow ^{4}$ He $\displaystyle +\gamma$

(6.68)

folyamat is megjelenik. A $^{4}He$ kötési energiája nagyobb, mint a deuteroné, ezért a héliumatommagra vonatkozó Boltzmann-egyenlet azt adja, hogy amint képződésük be tud indulni az említett kétrészecske szórásokon keresztül, arányuk gyorsan nő a deuteronéhoz képest. Feltéve, hogy az összes neutron héliumatommagokba tömörül, a héliumatommagok száma a neutronok felével lesz egyenlő. A barionikus anyag héliumhányada tehát:

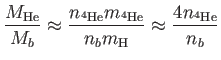$\displaystyle Y_{p}$	$\displaystyle \equiv$	$\displaystyle \frac{M_{\text{He}}}{M_{b}}\approx \frac{n_{^{4}\text{He} }m_{^{4}\text{He}}}{n_{b}m_{\text{H}}}\approx \frac{4n_{^{4}\text{He}}}{n_{b} }$
	$\displaystyle \approx$	$\displaystyle 2X_{n}\left( 0,07\text{ MeV}\right) =0,22 .$	(6.69)

ahol $M_{He}$ a héliumatommagok és $M_{b}$ a barionok össztömegét jelenti. A második sorban (6.63) és (6.64) egyenleteket használtuk.

**6.5. Ábra:** Az $Y\equiv Y_{p}$ héliumhányad az oxigén/hidrogén arány függvényében. Az alacsonyabb oxigéntartalmú rendszerek kevesebb (oxigénhez vezető) folyamaton estek át, így a bennük megfigyelt héliumhányad közelebb áll a nukleoszintézis kori értékhez. Az illesztés, amely szerint a kezdeti hányad $% Y_{p}=0.238$ , [13]-ból származik, az adatok pedig [14], [15], [16] és [17]-ből. A különböző csoportok által megfigyelt azonos rendszerekre kapott adatpontokat vonalak kötik össze. Az ábrát [12]-ből vettük.

A 6.5 ábra mutatja, hogy a megfigyelési adatok szerint a kezdeti héliumhányad

és

között van.

**6.6. Ábra:** Az elsődleges nukleoszintézis során keletkezett $^{2}$ He ( $\equiv$ D), $^{3}$ He és $^{7}$ Li atommagok számának hidrogénhez viszonyított aránya, illetve a $^{4}$ He tömeghányad az $\eta \equiv \eta _{b}$ (alsó vízszintes tengely), illetve $\Omega _{b}h^{2}$ (felső vízszintes tengely) paraméterek függvényében. A négyzetek az arányokra vonatkozó megfigyelésekkel való illeszkedést mutatják (kisebb négyzetek a nemszimmetrikus $95\%$ -os, a nagyobbak a szimmetrikus $95\%$ -os konfidencia-szinten). A vastagabb függőleges sávok a könnyű elemek megfigyelt hányadával, a vékonyabbak a kozmikus mikrohullámú háttérsugárzás anizotrópiáinak méréseiből származó adatokkal kompatibilis barionsűrűséget mutatják. A két sáv átfed. Az ábrát [18]-ból vettük.

**6.7. Ábra:** Az egyes atommaghányadok evolúciója $\eta _{b}=0,51$ esetén [19].

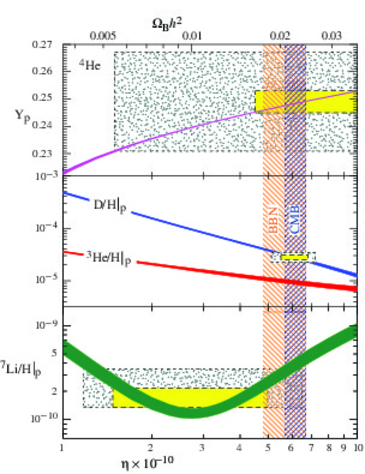
A deuteront más atommagokba konvertáló folyamatok hatékonysága a barionok mennyiségétől függ. Ha a barionsűrűség alacsony, akkor a deuteronok más atommagokkal történő találkozása kevésbé valószínű. Alacsony barionsűrűség esetén több deuteron marad a nukleoszintézis végére, mint magas barionsűrűség esetén. A 6.6 ábrán látható, hogy a nukleoszintézis végére megmaradt deuteron-hányad érzékenyen függ a barion mennyiségtől. A deutérium/hidrogén arány távoli rendszerekben történő megfigyeléséből jól lehet következtetni a barionmennyiségre.

A kezdeti deutérium/hidrogén arány mérhető olyan gázokban, amelyeken a távoli ( $z\approx 3$ ) kvazárok fénye áthatol. Az arányra a kvazár fényének gáz által okozott abszorpciójából lehet következtetni. Négy rendszerben megfigyelt deutériummennyiségből a deutérium/hidrogén arányra:

$\displaystyle D/H=3.0\pm 0.4\times 10^{-5}$

(6.70)

értéket kapták, amely a barionokat jellemző $\Omega _{b}$ kozmológiai paraméterre (ez $\Omega _{M}$ barionikus része) az

$\displaystyle \Omega _{b}h^{2}=0.0205\pm 0.0018$

(6.71)

értéket adja [20].

A hélium kialakulását követően megindul a nehezebb atommagok keletkezése is. Az atommagok Boltzmann-egyenletei integrálásának eredményét a 6.6 ábra mutatja. Az ábrán a $\eta _{b}$ paraméter függvényében látható az elsődleges nukleoszintézis során keletkezett atommagok számának hidrogénhez viszonyított aránya $^{2}$ H, $^{3}$ He és $^{7}$ Li-re, illetve az $Y_{p}$ héliumhányad. A 6.7 ábrán az egyes barion komponens-hányadok fejlődései láthatók rögzített $\eta _{b}$ -re a hőmérséklet függvényében. A nukleoszintézis alapvetően azért áll le, mert a nukleonok képződését eredményező reakciók ütemei a Hubble-paraméter alá csökkennek, így azok csak igen kis valószínűséggel folytatódnak a továbbiakban.

Távoli gázfelhőkben az elsődleges nukleoszintézis végére keletkezett egyes könnyű elemek hidrogénéhez viszonyított arányára a gázon keresztül haladó fény abszorciójának megfigyeléséből következtethetünk. E kezdeti arányok rendkívül érzékenyek az Univerzum korai, sugárzásdominált korszaka evolúciójának részleteire. Az előző alfejezetben láttuk, hogy az Univerzum lassú hűlése esetén kevesebb, míg gyors hűlése esetén több neutron marad. A gondolat folytatható. Több neutron esetén több deuteron képződhet. Az Univerzum lassú hűlése esetén (6.66)-(6.68) reakciókon keresztül több hélium képződik, ami nagyobb $Y_{p}$ értéket és kisebb detérium/hidrogén arányt ad, mint gyors hűlés esetén. Az atommagok keletkezése nem áll le a héliumatommagok létrejöttével. Lassúbb hűléskor a nukleoszintézis végére a nehezebb atommagok aránya több lesz a hidrogénéhez képest. Ha a reakciók ütemei sosem kerülnének a Hubble-paraméter alá, akkor az energetikailag legkedvezőbb vasatommagokba tömörülne az összes neutron.

A por és sugárzás energiasűrűsége $z\approx 3280$ vöröseltolódásnál, $% T\approx 9000$ K kőmérséklet körüli értéken lesz egyenlő, ezt követően az Univerzum a pordominált korszakba lép.

Szeged 2013-05-01