Atommagok ütközése

Az atommagok protonokból és neutronokból (nukleonokból) épülnek fel. A nukleonok számát adja meg az A tömegszám. Az atommag tömege $m = A m_a$, ahol $m_a$ az atomi tömegegység (1,6605 $\cdot 10^{-27}$ kg). A protonok számát a Z rendszám jellemzi. Az atommag elektromos töltése $Q = Z \cdot e$, ahol e az elemi töltés (1,6022 $\cdot 10^{-19}$ C).

A tapasztalat szerint az atommagok sugara és a tömegszám között az alábbi összefüggés érvényes:

$$r =  r_0 \cdot A^{-1/3},$$ (1.45)

ahol $r_0$ egy konstans (kb. 1,5 $\cdot 10^{-15}$ m). Ennek egy érdekes következménye az, hogy a nukleonok számsűrűsége (koncentrációja) állandó, mivel mind a mag tömege, mind a térfogata egyenesen arányos az A tömegszámmal. A nukleonkoncentrációra így kb. $10^{38}$ cm$^{-3}$ adódik. A mag tehát egy nagyon nagy, de állandó sűrűségű folyadékcseppre emlékeztet.

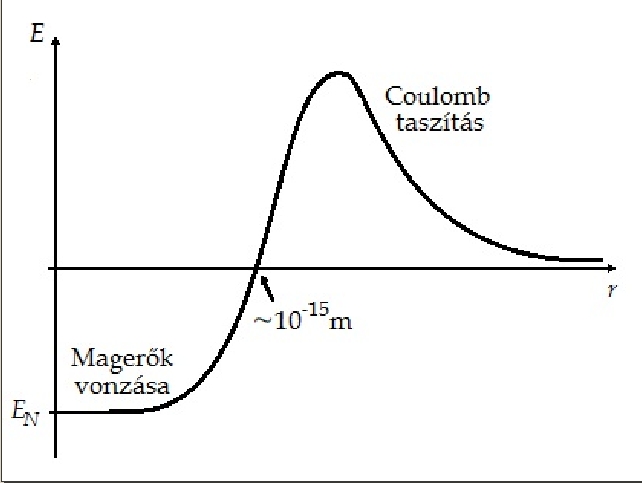
A nukleonok kötését a magerők biztosítják, amelyek rövid hatótávolságúak, csak az atommagon belül hatnak, de sokkal erősebbek a protonok közti elektromos (Coulomb-) taszításnál (1.3. ábra). A magerők egyformán hatnak proton-proton, proton-neutron és neutron-neutron részecskék között (magerők töltésfüggetlensége).

1.3. Ábra: A nukleonok kölcsönhatásai közül az atommag sugarán belül a magerők hatása érvényesül, azon kívül viszont a protonok közötti elektromos v. Coulomb-taszítás dominál.

Az atommag m tömege mindig kisebb, mint a magot alkotó nukleonok tömegének összege: $m < Z m_p + (A-Z) m_n$, ahol $m_p$ a proton, $m_n$ a neutron tömege. A $\Delta m$ tömegdefektus a mag kötési energiájának felel meg: $\Delta E = \Delta m c^2$, ennek értéke általában 10 - 100 MeV között van.

Két atommag egyesítésével nehezebb atommagok jöhetnek létre, ez a folyamat a magfúzió. Az 56-os tömegszámú vasnál könnyebb atommagok fúziójánál energia szabadul fel (exoterm reakció), ez amiatt van, mert a keletkező mag kötési energiája alacsonyabb, mint az ütköző magok kötési energiái együttvéve. A felszabaduló energia $Q = (m_1 + m_2 - m) c^2$, ahol $m_1$ és $m_2$ az ütköző magok, m a keletkező mag tömege. Az energiamegmaradáson túl a magfúziós folyamat során teljesülnie kell még az elektromos töltés és a barionszám megmaradási törvényének is.

Mivel az atommagok pozitív elektromos töltésűek, két mag közelítésekor először a Coulomb-taszítás érvényesül, ezért energiát kell befektetni ahhoz, hogy a két magot egymáshoz közelítsük. A Coulomb-taszítás miatti potenciális energia helyfüggését az 1.3. ábra mutatja. Az atommagok sugarának (kb. $10^{-13}$ cm) nagyságrendjébe eső kritikus távolság elérésekor a potenciálgát hirtelen megszűnik, és a magerők vonzó hatása kezd el érvényesülni. Atommagok ütközéséhez tehát elsősorban az elektromos töltések miatti Coulomb-taszítás okozta potenciálgáton kell átjutni.

A Coulomb-gát magassága a klasszikus elektrosztatika értelmében $E_C = Z_1 Z_2 e^2 / r^2$, ahol r a két ütköző nukleon távolsága (nagyságrendileg $10^{-13}$ cm). Az ütközést vizsgáljuk olyan koordináta-rendszerben, amely az egyik részecskéhez van rögzítve. Ez a célpont (target) atommag, a mozgó részecskét pedig szokás bombázó részecskének is nevezni.

A bombázó részecske kinetikus energiája $E_k = (1/2) m v^2$ = $(3/2) k T$, ahol v a részecske átlagsebessége, T a közeg hőmérséklete. A klasszikus fizika értelmében a potenciálgáton történő átjutás feltétele $E_k \geq E_C$. Ebből adódik a nukleonok klasszikus ütközéséhez szükséges hőmérséklet:

$$T =  {{2 Z_1 Z_2 e^2} \over {3 k r}, }$$ (1.46)

ami protonok ütközésére $10^{10}$ K-t ad. Mivel a Nap centrumában a hőmérséklet nagyságrendje csak $10^{7}$ K, a klasszikus fizika értelmében proton-proton ütközés nem mehetne végbe a Nap belsejében. Ezen még az sem segítene, ha figyelembe vennénk, hogy az átlagsebességhez képest gyorsabban mozgó részecskék is vannak, mert egyszerűen nincs elegendő számú atommag a Napban ahhoz, hogy akár egy ilyen reakció is megtörténhessen.