Next: Távolságmeghatározás Up: Pulzáló változócsillagok Previous: Mira és szemireguláris csillagok
Az instabilitási sávban lévő csillagok főleg radiálisan pulzálnak, azaz a sugár irányában kifelé és befelé történik a rétegek elmozdulása (Cooper & Walker 1994). A külső tartományban azonban körben haladó hullámok is kialakulhatnak, a földrengésekhez hasonlóan. A Nap oszcillációja is ilyen. Ez a pulzáció nemradiális módja. Ilyen esetben a csillag gömbszimmetriája megszűnik, az alakja változik.
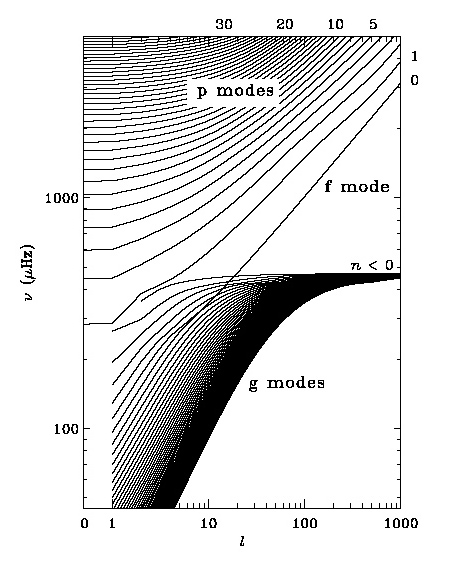
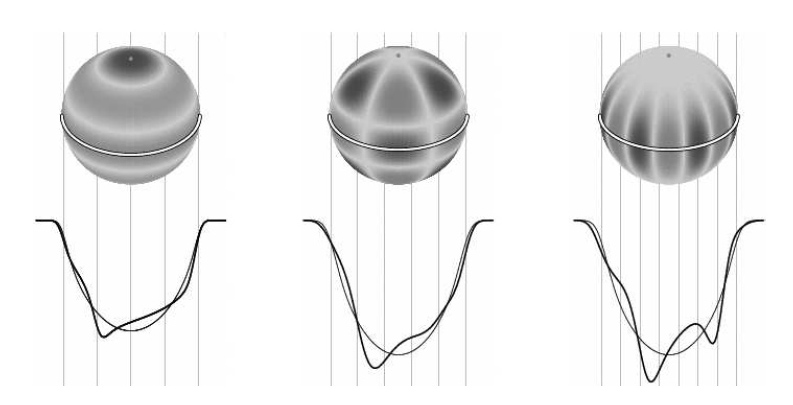
A nemradiális hullámok kétféleképp terjedhetnek. Az egyik típus nagyon alacsony frekvenciájú hanghullámnak felel meg, ezt p-hullámnak vagy nyomáshullámnak nevezik. A radiális rezgéseket szintén a nyomás kelti, így azok is p-hullámoknak tekinthetők, de ezt nem szokás hangsúlyozni. A nemradiális hullámok másik fajtájánál az oszcillációt a gravitáció és a felhajtóerő határozza meg, ezek a g-hullámok. Periódusuk általában hosszabb mint a p-hullámoké. A p-módusok amplitúdója a felszín közelében nagy, a g-módusoké viszont a csillag belsejében (3.29. ábra). A g-módusok jellemzők a fehér törpe pulzátorokra.
 |
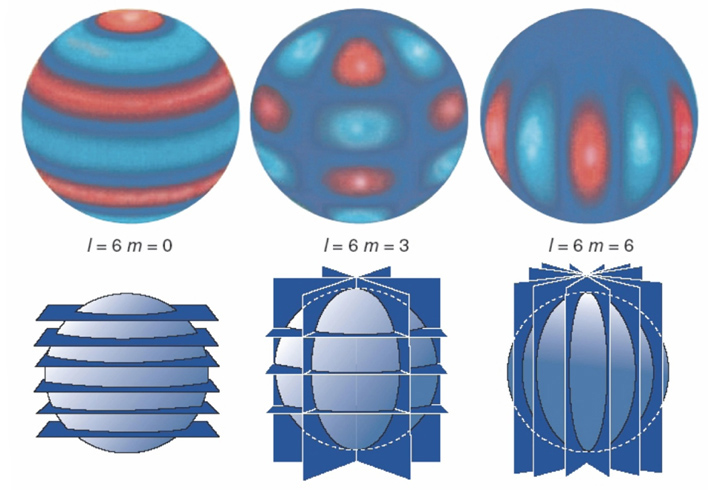
A nemradiálisan rezgő 3-dimenziós csillag módusainak jellemzésére három paramétert használunk:
- n: a radiális rend, sugárirányban a csillag belseje felé a csomófelületek száma.
- l: a fokszám, a csillag felszínén az összes csomóvonal száma. l=0 neve monopól módus, l=1 a dipól, l=2 a kvadrupól, l=3 az oktupól módus.
- m: az azimutális szám, a felszíni csomóvonalak közül a hosszúsági kör jellegű (pólusokon átmenő) csomóvonalak száma.
Az m értéke 2l+1 féle lehet -l és l
között. Ha
![]() ,
akkor haladó hullám megy körbe a csillagon direkt irányban (
,
akkor haladó hullám megy körbe a csillagon direkt irányban (![]() ) vagy
retrográd
irányban (
) vagy
retrográd
irányban (![]() ). Ha
a csillag gömbszimmetrikus, akkor a rezgési periódusa nem függ m-től.
Rotáció
és mágneses tér jelenléte esetén azonban az adott (n, l)
módus felhasad 2l+1
komponensre. A felhasadt komponensek közti távolság arányos a
rotáció frekvenciájával, relatív
amplitúdóik az inklinációtól (a látóirány és a rotációs tengely
szögétől) függnek.
). Ha
a csillag gömbszimmetrikus, akkor a rezgési periódusa nem függ m-től.
Rotáció
és mágneses tér jelenléte esetén azonban az adott (n, l)
módus felhasad 2l+1
komponensre. A felhasadt komponensek közti távolság arányos a
rotáció frekvenciájával, relatív
amplitúdóik az inklinációtól (a látóirány és a rotációs tengely
szögétől) függnek.
Radiális pulzációnál l=0, valamint n=0 esete az alaprezgés, n=1 az első felhang, n=2 a második felhang.
 |
 |
 |
 |
 |
 |
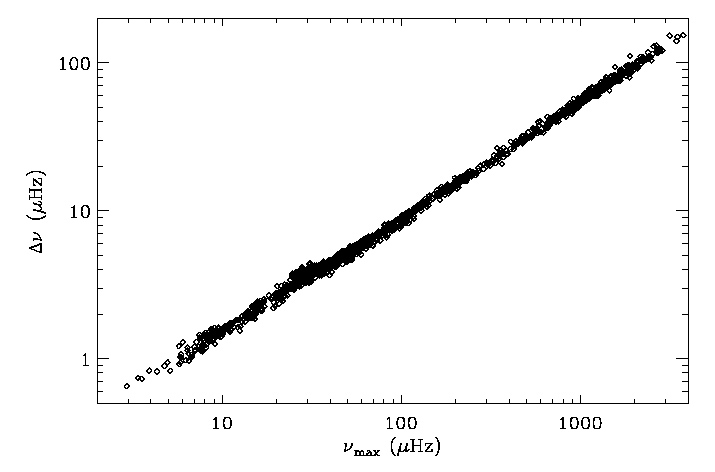
A Napban és a Nap típusú (solar-like) csillagokban az oszcillációt sztochasztikusan gerjeszti a konvekció (Bedding 2011). Számos, a Naptól jelentősen különböző csillagnál (pl. szubóriásoknál és vörös óriásoknál) is találtak ilyen pulzációt. A gerjesztés sztochasztikus természete miatt széles frekvenciatartományban jelentkeznek kis amplitúdójú, főként akusztikus p-módusok. A Nap esetében 1 és 4 mHz között (az 5 perces periódus közelében) rengeteg csúcs jelentkezik a frekvenciaspektrumban.
Az utóbbi években - különösen a Kepler űrtávcső nagyon pontos fotometriai mérései alapján - igen sok G és K színképosztályú óriáscsillagnál, de még félszabályos M óriások és vörös szuperóriások eseteiben (pl. Betelgeuze) is megfigyeltek Nap típusú pulzációt, jellemzően órás vagy még hosszabb periódusokkal.
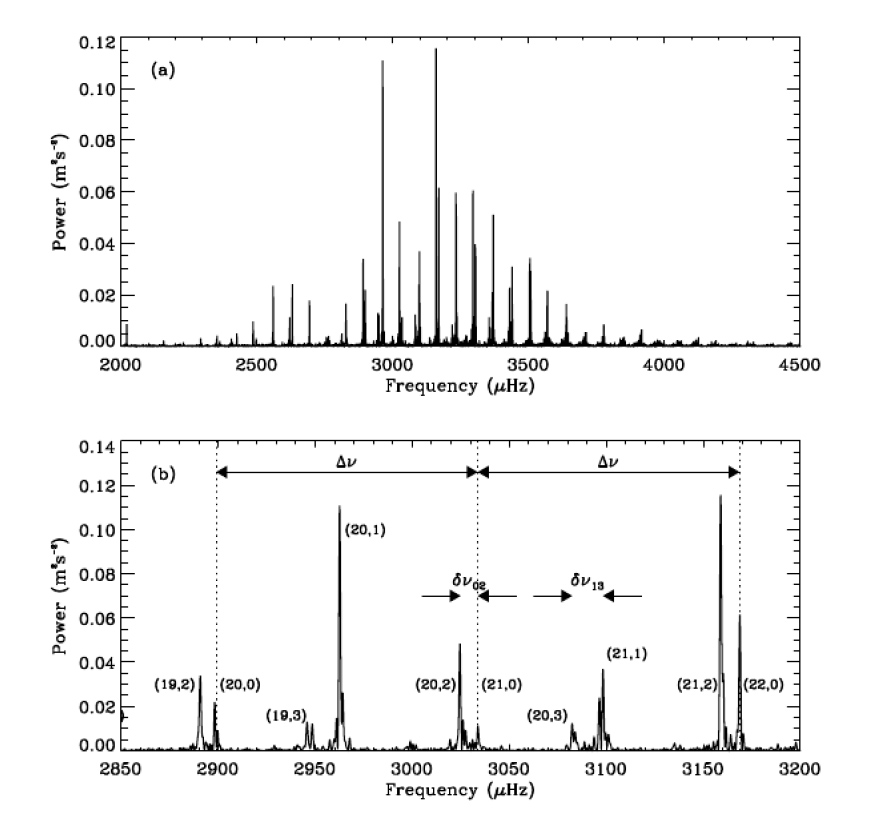 |
Ha a frekvenciaspektrumból meghatározzuk ![]() és
és ![]() értékét, akkor a
értékét, akkor a
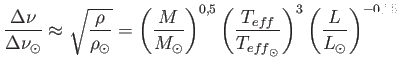 |
(3.7) |
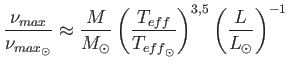 |
(3.8) |
képletek alapján a csillag tömegére, hőmérsékletére és luminozitására jó becslést adhatunk (Bedding 2011).
 |
A nemradiális pulzációt leíró egyenletek 3 dimenzióban
gömbszimmetrikus esetben, r a távolság
a csillag centrumától, ![]() a szélesség,
a szélesség, ![]() a hosszúság a felszínen, az
elmozdulások a 3
koordináta mentén (Kurtz 2006):
a hosszúság a felszínen, az
elmozdulások a 3
koordináta mentén (Kurtz 2006):
| (3.9) |
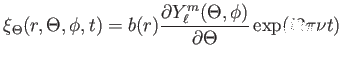 |
(3.10) |
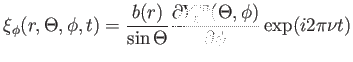 |
(3.11) |
a(r) és b(r) amplitúdók, ![]() az oszcilláció frekvenciája, t
az idő és
az oszcilláció frekvenciája, t
az idő és
![]() a szferikus harmonikusok, vagy gömbfelületi függvények:
a szferikus harmonikusok, vagy gömbfelületi függvények:
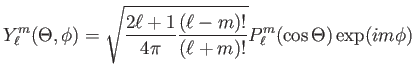 |
(3.12) |
ahol a Legendre-polinomok:
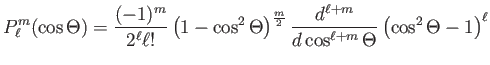 |
(3.13) |
Szeged 2013-05-01