A Fourier-analízis gyakorlati megvalósítása

Feladat az időből a frekvenciatartományba való átalakítás, a

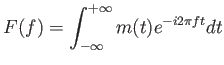$$F(f)=\int_{-\infty}^{+\infty} m(t) e^{-i2\pi ft} dt$$ (3.42)

komplex Fourier-transzformáció megvalósítása.

Mivel a gyakorlatban az adatsor hossza véges, és időben diszkrét méréseket tartalmaz, a diszkrét Fourier-transzformáció (DFT) használatos:

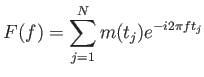$$F(f)=\sum_{j=1}^N m(t_j) e^{-i2\pi ft_j}$$ (3.43)

Az f frekvenciához tartozó amplitúdó kiszámítása az

$$A(f)=\left [ (2/N\; C_f)^2 + (2/N\; S_f)^2 \right ]^{1/2}$$ (3.44)

kifejezéssel történik, ahol N az adatsor pontjainak száma, és

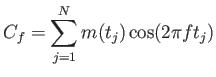$$C_f=\sum_{j=1}^N m(t_j) \cos (2\pi f t_j)$$ (3.45)

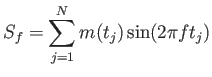$$S_f=\sum_{j=1}^N m(t_j) \sin (2\pi f t_j)$$ (3.46)

A fázist a

$$\phi=arc tg (-S_f/C_f)$$ (3.47)

kifejezés adja meg. Sajnos általában a fázis meghatározásának nagy a hibája, sokszor eléri a tized radiánt. Gyakori megoldás, hogy a DFT-vel kapott frekvenciával legkisebb négyzetes illesztést végzünk, és ebből határozzuk meg a fázist.

Az adateloszlásra jellemző spektrálablak-függvény kiszámítása a

$$W(f)=\left [ 1/N \sum_{j=1}^N \cos (2\pi f t_j) \right ]^2 + \left [ 1/N \sum_{j=1}^N \sin (2\pi f t_j) \right ]^2$$ (3.48)

kifejezéssel történik (power spektrum realizációban). A Fourier-frekvenciaspektrum a Nyquist-frekvenciára periodikusan ismétlődik, így a

$$f_N=1/2\Delta t$$ (3.49)

frekvenciánál nagyobb értékek meghatározása elvi akadályokba ütközik. Ugyanakkor, ha a mintavételezés nem egyenletes időközű, a Nyquist-határ kitolódik, $1/2 \Delta t_{min}$ értéknél nagyobb lesz.

A Fourier-analízisnek rendkívül nagy irodalma van, még akkor is, ha csak a csillagászati szakfolyóiratokra szorítkozunk. Több algoritmust közöltek a DFT kiszámítására (Deeming 1975, Scargle 1982, Kurtz 1985, Szatmáry 1986).

Sokan vizsgálták a Fourier-módszer és más periódusmeghatározási eljárás kapcsolatát, matematikai hasonlatosságát. Külön említést érdemelnek a frekvencia meghatározási pontossága, a szignifikancia szint megadása céljából készült dolgozatok.

Amennyiben a vizsgált adatsorban nagyon közeli frekvenciák vannak, azok a Fourier-spektrumban nem mindig különülnek el, az összeolvadt kettős csúcs komponenseinek helyére korrigálni kell.

Ha az adatsorban a mintavételezés igen egyenetlen, akkor a spektrálablak-függvényben - és így a csillag frekvenciaspektrumában is - sok mellékcsúcs jelenik meg, megnehezítve a valódi fényváltozást leíró frekvenciák azonosítását. Próbálkoztak már ``adatkompenzált'', DCDFT eljárást kidolgozni (Ferraz-Mello 1981), de nem nagyon terjedt el.