Fehérítés

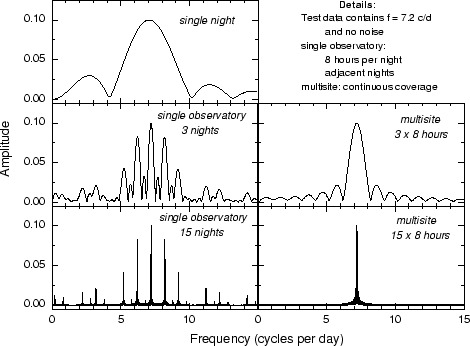
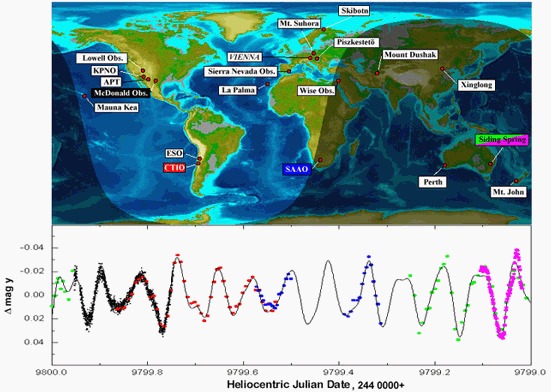
A gyakorlatban legtöbbször messze nem egyenletes időközű az adatsor. A rövid periódusú változócsillagok esetében még az egy éjszakán belüli mérési pontokat sem sikerül egyforma időnként felvenni, a nappalok miatti űrök pedig csak nagy erőfeszítéssel megszervezett és az egész Földre kiterjedő nemzetközi megfigyelési kampányokkal küszöbölhetők ki (3.93. és 3.94. ábra).

3.93. Ábra: A hosszabb adatsor keskenyebb frekvenciacsúcsokat eredményez (bal oszlop). Az 1 ciklus/nap (c/d) távolságokra lévő hamis csúcsok kiküszöbölésére csökkenteni kell az adatsorban a (nappali) űrök hosszát, ez a több földrajzi hosszúságon lévő megfigyelők együttműködésével érhető el (http://www.univie.ac.at/tops/dsn/).

3.94. Ábra: Nemzetközi összefogás $\delta$ Scuti csillagok megfigyelésére (http://www.univie.ac.at/tops/dsn/).

Elterjedt az időtartományban való fehérítés. A mérési adatsor frekvenciaspektrumából meghatározott - általában a legnagyobb amplitúdójú - komponenssel, melynek ismert a periódusa, amplitúdója és fázisa, az eredeti adatsort fehérítjük egyszerű levonással (prewhitening). E módszernek azonban vannak buktatói. Nem biztos, hogy a legnagyobb amplitúdójú csúcshoz tartozik a valós fényváltozási ciklus, ugyanis nagy mérési zaj, nagy űrök és többmódusú oszcilláció esetén a hamis csúcsok felerősödhetnek. Másik probléma a fehérítő színuszfüggvény fázisának meghatározása. Sajnos ezt az értéket csak kis pontossággal lehet megadni, pedig a fehérítés utáni adatsor jellege igen érzékeny erre.

Az időbeli fehérítést alkalmazza például a sokak által használt PERIOD04 program (Lenz & Breger 1995), ha már a fázis ismert.

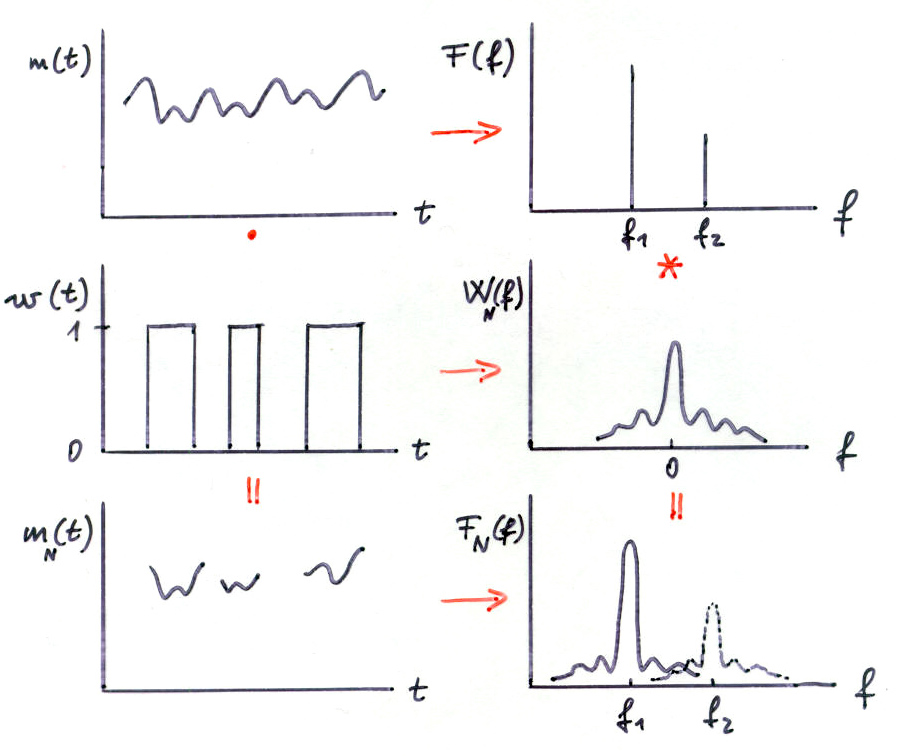
Az egyenetlen adateloszlást jellemzi a spektrálablak-függvény. Ez ``ül rá'' minden, valójában Dirac-delta frekvenciakomponensre, hiszen a számított spektrum az a valódi spektrum és a spektrálablak-függvény konvolúciója (3.95. ábra). A frekvenciatartományban történő dekonvolúciót fehérítésnek nevezzük, ez régóta ismert, de matematikailag körülményes, és sok gépidőt kíván.

3.95. Ábra: Mivel a fénygörbét csak néhány időablakban tudjuk mintavételezni, a frekvenciakomponensek Dirac-delta helyett a spektrálablak mintázatát mutatják.

A frekvenciatérben fehérít a CLEAN-módszer is, amely nagyon hatékonyan kiszűrheti a hamis csúcsokat (Roberts, Lehár, Dreher 1987). Ugyanakkor vigyázni kell vele, mert az eljárás minden dekonvolúció során mindig a maradványspektrum legmagasabb csúcsát tekinti következő komponensnek.