Fourier-analízis

A Fourier-transzformáció széles körben használatos a periodikus jelek vizsgálatára. A csillagászaton belül különösen nagy a jelentősége a változócsillagok fénygörbéje periódusainak meghatározásánál. Legyen a mért időben változó mennyiség, például a csillag fényessége m(t). Sok esetben nem szükséges a fénygörbére az igen általános

$$m(t)=<m(t)>+\sum_{n=1}^N A_n (t) \cos \left [ 2\pi f_n (t) t + \phi_n (t) \right ]$$ (3.25)

alakot feltételezni (az indexelt függvények közelítése a mérési adatokból valamiféle optimalizálási eljárással általában rendkívül számításigényes feladat lenne).

Egyszerűbb az analízis, ha a fénygörbe több, egymástól független és stacionárius harmonikus oszcilláció szuperpozíciója:

$$m(t)=\sum_{n=1}^N A_n \cos \left [ 2\pi f_n t + \phi_n \right ]\hskip1cm (N<\infty)$$ (3.26)

Az ismeretlen $A_n$, $f_n$, és $\phi_n$ meghatározásában alapvető jelentősége van a Fourier transzformációnak, melynek definíciója folytonos esetre:

$$FT \left [ m(t) \right ] = F(f) := \int _{-\infty}^{+\infty} m(t) e^{-i2\pi f t} dt$$ (3.27)

A (3.26) kifejezés Fourier-transzformáltja analitikusan megadható:

$$F(f)=\sum_{n=1}^N A_n/2 \left [ e^{i\phi_n} \delta (f-f_n) + e^{-i\phi_n} \delta (f+f_n) \right ]$$ (3.28)

Csak a pozitív frekvenciákat tekintve látszik, hogy N számú oszcilláció N helyet jelöl ki a spektrumban.

Egy időben folytonos függvény értékeit azonban csak diszkrét időpontokban ismerhetjük. A mérési időközök még egy megfigyelési sorozatban sem mindig egyenlők. Előfordulhat, hogy egy csillag fényességének mérhetőségére hónapokig kell várni.

A (3.27) diszkrét változatának (DFT, Deeming 1975) kifejezése

$$DFT \left [ m(t) \right ] = D(f) := \sum_{j=1}^N m(t_j) e^{-i2\pi f t_j}$$ (3.29)

amely nagymértékben függ az adateloszlástól. D(f)-et találóan hamis spektrumnak is nevezik, a továbbiakban ezt igazoljuk. Vezessük be az

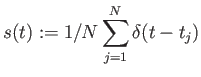$$s(t):=1/N \sum_{j=1}^N \delta (t-t_j)$$ (3.30)

ún. mintavételező, és az $m_s (t) = m(t) s(t)$ mintavételezett függvényt. Utóbbi az

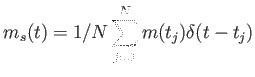$$m_s(t)=1/N \sum_{j=1}^N m(t_j) \delta (t-t_j)$$ (3.31)

alakban írható. A spektrálablak

$$W(f):=FT \left [ s(t) \right ] = \int_{-\infty}^{+\infty} s(t) e^{-i2\pi f t} dt$$ (3.32)

definícióját felhasználva felírhatjuk a mintavételezett függvény Fourier-transzformáltját:

$$FT \left [ m_s(t) \right ] = F(f) * W(f)$$ (3.33)

amely éppen (3.29)-gyel egyezik. Elmondhatjuk tehát, hogy egy $m(t_j)$ j=1, ..., N adatsor diszkrét Fourier transzformáltja megegyezik az m(t) mintavételezettjének folytonos Fourier- transzformáltjával, azaz

$$D(f)= FT \left [ m_s(t) \right ] = 1/N \sum_{j=1}^N m(t_j) e^{-i2\pi f t_j}$$ (3.34)

továbbá

$$W(f)=FT \left [ s(t) \right ] = 1/N \sum_{j=1}^N e^{-i2\pi f t_j}$$ (3.35)

Az alkalmazott normálási tényezők mellett

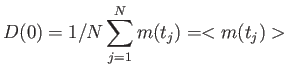$$D(0)=1/N \sum_{j=1}^N m(t_j) = <m(t_j)>$$ (3.36)

és W(0)=1.

Jelölje T a mintavételezés időtartamát, így $T = t_N -t_1$ , és vezessük be a $h(t)=1$ ha $t_1\leq t \leq t_N$, különben $h(t)=0$ ún. ablakfüggvényt. Jelöljük $m_h(t)$-vel azt a függvényt, amely a $[t_1, t_N]$ intervallumon azonos m(t)-vel, másutt zérus, így $m_h(t) = m(t) h(t)$. Ennek a ``csonka'' függvénynek a Fourier-transzformáltja a konvolúciótétel szerint:

$$FT \left [ m_h(t) \right ]=F(f) * H(f)$$ (3.37)

ahol

$$H(f)=FT \left [ h(t) \right ] = \sin (\pi ft)/(\pi f) e^{-i\pi f(t_1+t_N)}$$ (3.38)

a spektrálablak folytonos és véges időtartamú adatsor esetén. A (3.37) konvolúció az F(f) tulajdonságainak keveredését (spektrális áteresztését) eredményezi ott, ahol H(f) számottevő.

A diszkrét mintavételezésből eredő nem zérus frekvenciafelbontás a W(f) (f=0-nál lévő) főcsúcsának szélességével egyezik meg, amely közel azonos a H(f) főcsúcsának szélességével, feltéve ha a mintavételezés nem túlságosan egyenetlen, és így

$$\delta f \approx 1/T$$ (3.39)

Egyenközű adatsor esetén a mintavételezés elméletéből következik, hogy azt a függvényt, amelynek Fourier-transzformáltja zérus minden $\vert f\vert \geq f_N$ helyen, teljesen meghatározzák az egyenlő, de bizonyos $1/2f_N$ -nél nem hosszabb intervallumokon felvett értékei. A maximális frekvencia, amelyet meg lehet határozni a $\Delta t$ mintavételezési időközből, az ún. Nyquist-frekvencia:

$$f_N=1/2\Delta t$$ (3.40)

3.92. Ábra: Szimulált adatsor (pontok) és illesztésük f=0,123456789 c/d frekvenciával. A folytonos vonal az f=2,123456789 c/d frekvenciával szintén jól illeszkedik, de hamis, a mintavételezés nem elég sűrű hozzá, a Nyquist-frekvencián túl van (Aerts et al. 2010).

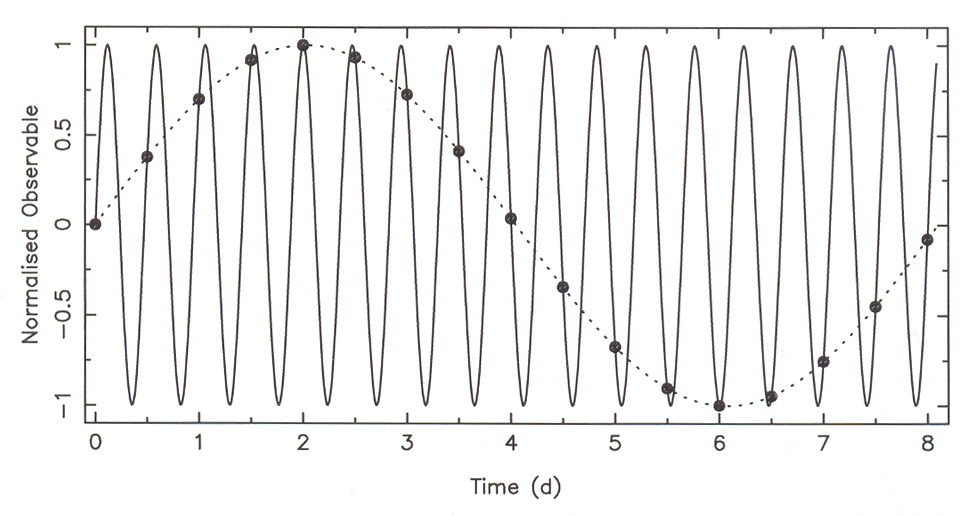Nemegyenközű adateloszlás esetén a maximális frekvenciáról a mintavételezés elmélete nem mond semmit. Ha az adatsor egyenközű, de hiányoznak mérési pontok, az elmélet szerint az adatok olyan függvényt határoznak meg, amelynek Fourier transzformáltja zérus minden

$$\vert f\vert \geq 1/2\Delta t_{max}$$ (3.41)

helyen, ha $\Delta t_{max}$ a legnagyobb időköz. Az ennél kisebb időközök biztosan hordoznak információt az $1/2 \Delta t_{max}$-nál nagyobb frekvenciákon, valamennyi információ az $1/2 \Delta t_{min}$ körül is található, ha $\Delta t_{min}$ a legkisebb időköz. A spektrumot tehát az $1/2 \Delta t_{min}$ frekvencia felett nagyon óvatosan kell vizsgálni.