Matematikai alapok

Egy valós m(t) függvény (általában komplex) g(t) ún. analizáló hullámra vonatkozó wavelet-transzformáltján a következő kétváltozós kifejezést értjük:

$$W(a,b)=1/\sqrt{a} \int_{-\infty}^{+\infty} m(t) \cdot g^{\ast}\left [ (t-b)/a\right ] dt$$ (3.50)

amely a

$$H=\{ (b,a) \vert a \in \Re, a > 0, b \in \Re \}$$ (3.51)

nyitott félsíkon értelmezhető.

Nemegyenközű adateloszlás esetén egy konkrét realizáció a következő formában történhet:

$$W(\tau ,f)=\frac{1}{C}\sum_{k=1}^N m(t_k) \cdot e^{-i2\pi f(t_k-\tau)} \cdot e^{\frac{(t_k-\tau)^2}{\Delta\tau^2}}$$ (3.52)

ahol

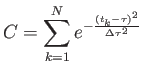$$C=\sum_{k=1}^N e^{-\frac{(t_k-\tau)^2}{\Delta\tau^2}}$$ (3.53)

Az itt szereplő $\tau$ a korábbi b változónak, ill. az 1/f idő dimenziójú mennyiség az a változónak felel meg. A $\tau$ az időbeli eltolás, $\Delta\tau$ pedig a Gauss-ablak félszélességével arányos. A fenti kifejezés szerint az ablak szélessége a frekvenciától független állandó. Általában azonban az ablakszélességet úgy választják meg, hogy megegyezzen a próbaperiódussal, azaz $\Delta\tau \approx P = 1/f$.

A (3.52) kifejezésben egy fix $\tau$ mellett kiemeljük a $\tau \approx t_k$ időponthoz közeli függvény tulajdonságokat az adateloszlástól és a próbaperiódustól függő szélességben, és képezzük a Fourier-spektrumot. Amennyiben a $t_k$-hoz közeli időben az érvényes frekvencia f', úgy a wavelet-transzformált amplitúdója nagy a $(t_k ,f')$ pont felett.

Az analizáló hullám, vagy magfüggvény alakja nagyon sokféle lehet, attól függően, hogy a vizsgálandó függvénynek milyen tulajdonságai vannak. A transzformáció - általánosságánál fogva - sok segítséget nyújthat előzetes tájékozódáshoz a legkülönfélébb változások felismerésében.