A wavelet-analízis

A Fourier-transzformációval lényegében csak a fénygörbe egészére jellemző additív harmonikusokat szemléltethetjük. Az idő-frekvencia módszerekkel a periódus, az amplitúdó és a fázis időbeli változását is nyomon követhetjük.

Idő-frekvencia eloszlási függvényt nagyon sokfélét definiáltak. Először az ablakozott Fourier-analízist használták (Gábor-transzformált, ha Gauss-görbe az analizáló ablak). Ennél az ablak - amit végigcsúsztatunk az adatsoron, és csak a benne lévő adatokat vizsgáljuk - időben állandó szélességű, míg a wavelet-transzformációnál minden egyes időbeli elcsúsztatáson belül az ablak szélessége változik, a próbafrekvenciával fordítottan (a próbaperiódussal egyenesen) arányos. Emiatt a wavelet esetén az idő-frekvencia felbontás erősen változó: kis frekvenciáknál időben nyúlnak szét az amplitúdócsúcsok, nagyobb frekvenciákon pedig a frekvencia mentén (3.96. ábra). Erre nagyon figyelni kell a wavelet-térképek értelmezése során.

3.96. Ábra: Idő-frekvencia felbontás az ablakozott Fourier- (balra) és a wavelet-transzformált (jobbra) esetében. A Heisenberg-féle határozatlansági relációhoz hasonlóan $\Delta t \cdot \Delta \omega$ állandó $\geq 1/2$ (Szatmáry 2012).

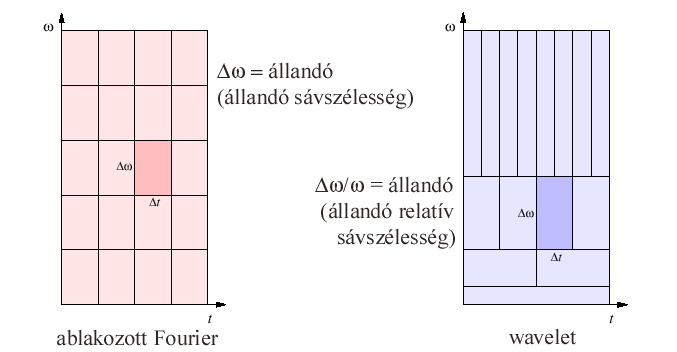Az ún. wavelet-transzformáció története hosszú időre nyúlik vissza, de sokáig csak matematikai vizsgálatok tárgya volt. Később az akusztikában, a zenében, a geofizikában, a meteorológiában, az orvostudományban használták különféle elnevezésekkel. Például a Föld atmoszférájában terjedő, kozmikus eredetű rádiójelek egy részének (a whistlereknek) az időbeli frekvenciaváltozását dinamikus (frekvencia-idő-amplitúdó) spektrumok térképeivel tanulmányozták.

Manapság tág fogalmat takar a wavelet-transzformáció. Egyre több területen használják, sokféle alakban és több dimenzióban. Az egyik fő alkalmazás a képfeldolgozás. Speciálisan a csillagászatban többször galaxisok térbeli eloszlásának vizsgálatát végezték segítségével. A wavelet-eljárások egyre gyakoribbak a turbulenciák és a fraktálok matematikai elemzésénél és a telekommunikáció területén is. Számos könyv jelent meg az utóbbi években a wavelet-analízisről és alkalmazásairól.

A módszert sokszor használják a napfizikusok is. Korábban a ``sonagram'' nevű idősor darabolásos Fourier-módszerrel próbálták a naptevékenységi ciklusok változását vizsgálni. Az 1990-es évektől a wavelet-transzformáció megjelent a napfoltciklusok periodicitásának analízisénél is.

A wavelet-analízis a változócsillagok fénygörbéjének elemzéséhez mintegy két évtizede használatos. Olyan adatsorokra alkalmazható leginkább, amelyekben alig vannak kisebb űrök. A világon az elsők között alkalmaztuk a wavelet-módszert hosszú periódusú pulzáló változókra, mirákra és félszabályos csillagokra.