Next: A wavelet-térkép Up: A wavelet-analízis Previous: Matematikai alapok
Legyen m(t) a csillag fényváltozását leíró függvény. Az f frekvenciához és a ![]() időeltolási
paraméterhez tartozó wavelet-transzformáció:
időeltolási
paraméterhez tartozó wavelet-transzformáció:
![$\displaystyle W(f,\tau)=\sqrt{f} \int_{-\infty}^{+\infty} m(t) \cdot g^{\ast}\left [ f(t-\tau)\right ] dt$](img651.png) |
(3.54) |
az ún. Morlet-féle analizáló wavelet egy módosított Gauss-görbe:
| (3.55) |
ahol
![]() és általában
és általában ![]() (a c értéke a frekvencia- és időbeli felbontás
paramétere).
(a c értéke a frekvencia- és időbeli felbontás
paramétere).
A gyakorlatban a DFT-hez hasonlóan bevezethető a diszkrét wavelet-transzformáció (DWT), amely szerint az amplitúdó spektrum:
![$\displaystyle W(f,\tau)=\left [ f \cdot C(f,\tau)^2 + f \cdot S(f,\tau)^2\right ]^{\frac{1}{2}}$](img655.png) |
(3.56) |
ahol
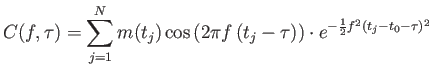 |
(3.57) |
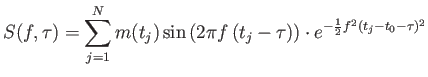 |
(3.58) |
és ![]() az adatsor első eleméhez tartozó idő.
az adatsor első eleméhez tartozó idő.
A Gauss-ablak félszélessége a próbaperiódussal arányos (P=1/f), nem pedig állandó érték, mint
a Fourier-módszernél. Az ablakot ![]() értékkel toljuk el az adatsor elejétől a végéig, és minden
eltolásra kiszámoljuk a frekvenciaspektrumot.
értékkel toljuk el az adatsor elejétől a végéig, és minden
eltolásra kiszámoljuk a frekvenciaspektrumot.
Fontos megjegyezni, hogy a wavelet nem egyszerűen egy adatsor feldarabolásos (ablakozott) Fourier-módszer! A csúsztatott ablakozás mellett alapvető, hogy az ablak szélessége mindig illeszkedik a keresett periódus hosszához. Ennek következtében a frekvenciaspektrumban a csúcsok félszélessége nem egyforma, mint a Fourier-analízisnél, hanem a frekvenciával arányosan növekszik. Ez az aszimmetria egyetlen csúcs esetében is jelentkezik, a nagyobb frekvenciájú oldala ``laposabb''.
Szeged 2013-05-01