A wavelet-térkép

A wavelet-transzformációval kapott frekvencia-idő-amplitúdó adathármasok egy felületként ábrázolhatók, ezt nevezzük wavelet-térképnek. Ez azt szemlélteti, hogy a különböző frekvenciájú, illetve periódusú fényváltozások mikor és milyen amplitúdóval vannak jelen a fénygörbében.

A fénygörbe alapos szemrevételezése után a vizsgált adatsornak először mindig a Fourier-spektrumát számoljuk ki, amelynek alapján tájékozódni lehet a periódusok helyéről, és megválaszthatóak a wavelet-analízis paraméterei (időbeli és frekvenciabeli felbontások, lépésközök, határok).

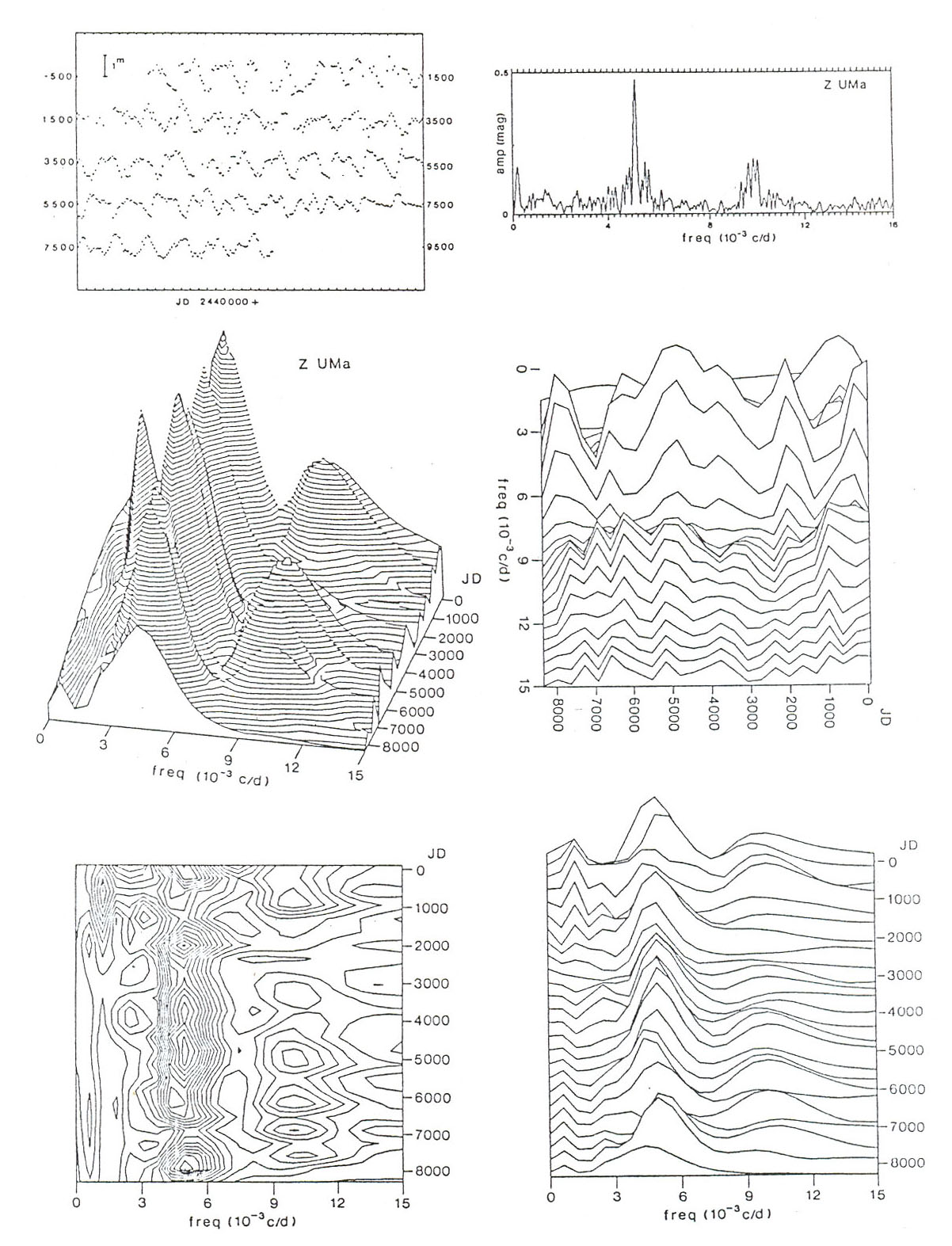
A módszer szemléltetésére a Z UMa SRb típusú csillag példáján keresztül bemutatjuk a wavelet-térképet. A 3.97. ábrán felül a fénygörbe, mellette a teljes adatsor Fourier-spektruma látható. A wavelet-térképet érdemes többféle nézőpontból ábrázolni. Szerencsére számos szoftver alkalmas arra, hogy a frekvencia-idő-amplitúdó adathármasok által alkotott felületet tetszőleges helyzetben kirajzolja.

A bal oldali középső szintvonalas ábra a perspektivikus térkép, amelyen ``amplitúdóhegyek'' és ``-dombok'' jól megfigyelhetők. Alatta szerepel ennek felülnézete, amelyen jobban nyomon követhető a csúcsok pozíciója. A jobb oldalon középen lévő ábra azt mutatja, hogy az egyes frekvenciákhoz tartozó amplitúdók hogyan változnak az időben, végül az alatta található ábra a Fourier-spektrum időbeli változását tárja elénk.

A cél az, hogy a térképek alapján olyan jelenségeket mutassunk ki (pl. modulációk, fázisugrás, módusváltás), amelyek a hagyományos Fourier-módszerrel nem tanulmányozhatók kielégítő részletességgel. Azonban a bemutatott példán látható, hogy a térkép rendkívül bonyolult. A wavelet-módszer tulajdonságainak a részletes vizsgálata nélkül hamis következtetésekre juthatunk, különösen az amplitúdó változására vonatkozóan.

A különféle jelenségeket reprezentáló teszt-adatsorok wavelet-térképeinek tulajdonságai mellett alapvető az adatok időbeli eloszlásának hatása az amplitúdó szempontjából. Mint ahogyan a Fourier-módszernél, itt is tapasztalható, hogy a mintavételezés romlásával, űrök jelenlétekor az amplitúdóspektrum, ill. -térkép ``kicsipkéződik'', az űrök idején hirtelen nullára csökken, és sokszor amplitúdómodulációhoz hasonló képhez vezet. Emiatt egy speciális fehérítő eljárást vezethetünk be (Szatmáry 1994). Ennek lényege, hogy az adateloszlás, adathiányok miatti amplitúdócsökkenésre úgy következtethetünk, hogy az eredeti adatok időpontjaiban egy szinuszt vagy több szinuszfüggvény eredőjét generálunk (a periódusokat, amplitúdókat és fázisokat az adott csillag Fourier-spektrumából határozzuk meg előzőleg). Ennek a ``teszt'' fénygörbének a wavelet-térképe már mutatja az adathiányok miatti amplitúdómintázatot. A ``teszt'' és az eredeti wavelet összehasonlításával kiszűrhetők a nem valós amplitúdóváltozások.

3.97. Ábra: A Z UMa fénygörbéje, Fourier-spektruma és wavelet-térképe több vetületből (Szatmáry 1994).

3.98. Ábra: A KIC 2582664 csillag fénygörbéje a Kepler űrtávcső adatai alapján (Bódi 2012).

3.99. Ábra: A KIC 2582664 csillag wavelet térképei változó idő-lépésköz (fent), frekvencia-lépésköz (középen) és idő-frekvencia felbontás paraméter (lent) esetén (Bódi 2012).