Az adott spirálkar-indikátorok távolságának minél pontosabb meghatározása alapvető fontosságú a spirálstruktúra meghatározásában. A távolságok meghatározására mára már számos módszer látott napvilágot, lehet geometriai, fotometriai vagy egyéb módszert alkalmazni. Először néhány egyedi objektumokra, csillagokra használt módszert, majd pedig a csillagcsoportok, nyílthalmazok távolságának meghatározását mutatom be.
Az asztrometiai távolságmérés alapja a parallaxis szögének meghatározása. A parallaxis jelensége azért lép fel, mert az égitestet a tér különböző pontjaiból más és más irányban látjuk, látszólag elmozdul. Attól függően, hogy a megfigyelő elmozdulását milyen tényező okozza, beszélünk napi, évi és szekuláris parallaxisról. A napi parallaxis azért jön létre, mert a Föld két különböző pontján álló megfigyelők más irányból látják a megfigyelt égitestet. Az évi parallaxis azért jön létre, mert a Földünk kering a Nap körül. Ennek következtében egy év alatt a földi megfigyelő úgy látja, mintha a megfigyelt égitest egy kis ellipszist írna le az égen, amelyet parallaktikus ellipszisnek hívunk.
A látszólagos ellipszis szögátmérője mérhető, ebből pedig meg lehet
határozni a távolságot egy egyszerű összefüggéssel. Ha d a csillag
távolsága, ![]() a látószög radiánban, s a két megfigyelés
helyének távolsága és mivel egy csillag távol van,
a látószög radiánban, s a két megfigyelés
helyének távolsága és mivel egy csillag távol van, ![]() kicsi
szög, ezért
kicsi
szög, ezért
![]() , a távolság a következő
módon határozható meg:
, a távolság a következő
módon határozható meg:
| (4) |
A parallaxis szögének meghatározása meglehetősen nehéz feladat. Ezen
kívül számos jelenség nehezíti a pontos méréseket: a csillagok sajátmozgása,
a fény aberrációja, stb. Ez a módszer a közeli (50![]() 100 pc távolságú)
csillagok esetén ad elegendő pontossággal távolságot, mivel a távoli
csillagok kevésbbé mozdulnak el, így ezek parallaxisa is kis mértékű.
Tehát ahhoz, hogy szinte az egész galaxisunkat ``belássuk'', más
módszert kell használni.
100 pc távolságú)
csillagok esetén ad elegendő pontossággal távolságot, mivel a távoli
csillagok kevésbbé mozdulnak el, így ezek parallaxisa is kis mértékű.
Tehát ahhoz, hogy szinte az egész galaxisunkat ``belássuk'', más
módszert kell használni.
Pusztán fényességméréssel is lehet távolságot meghatározni. A Hipparkhosz
által meghatározott magnitúdóskálát Pogson kapcsolta össze a fluxussal.
Így az ő nyomán a következőt használjuk, ahol ![]() ,
, ![]() két
csillag fluxusa,
két
csillag fluxusa, ![]() ,
, ![]() a látszó fényességük:
a látszó fényességük:
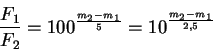 |
(5) |
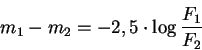 |
(6) |
Egy csillag látszó fényességét 10 pc távolságban abszolút fényességnek
hívjuk. Ezt beírva a fenti képletbe egy csillagra, valamint behelyettesítve,
hogy a fluxus a távolság négyzetével fordítva arányos a következőkre
jutunk:
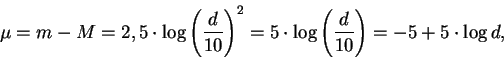 |
(7) |
| (8) |
Abban az esetben, ha a csillag és a megfigyelő között intersztelláris
extinkció is fellép, akkor a távolságmodulus értéke a következő módon
módosul:
| (9) |
| (10) |
Ez a módszer csak akkor használható, ha ismert egy csillag abszolút fényessége. Tulajdonképp elmondhatjuk, hogy a különböző fotometriai távolságmérési módszerek lényegében az abszolút fényesség meghatározásának módjában térnek el.
Néhány csillag abszolút fényességét közvetlenül is meg tudjuk határozni.
Ilyenek például az RR Lyrae, valamint a
![]() típusú csillagok. Ezeknél a változócsillagoknál a periódus-fényesség
relációból, a fényváltozás periódusának ismeretében meghatározható
az abszolút fényesség, a látszó fényesség egyidejű mérésével pedig
kiszámítható a csillag távolsága. A periódus-fényesség reláció általános
alakja a következőképpen néz ki:
típusú csillagok. Ezeknél a változócsillagoknál a periódus-fényesség
relációból, a fényváltozás periódusának ismeretében meghatározható
az abszolút fényesség, a látszó fényesség egyidejű mérésével pedig
kiszámítható a csillag távolsága. A periódus-fényesség reláció általános
alakja a következőképpen néz ki:
| (11) |
Ez a módszer tehát nagyon jól használható a spirálkar-indikátorok egyik fajtájára, a cefeida változócsillagokra. Az így meghatározott távolságot cefeida parallaxisnak is szokás nevezni. Mivel a cefeida változók óriás csillagok nagy luminozitással, így a távolabbiak is megfigyelhetőek.
Más csillagok esetén is van mód az abszolút fényesség meghatározására.
A csillagok színe, színképe információt ad a luminozitásról, sőt az
esetleges fénygyengítés mértékéről is. A Hertzsprung![]() Russell-diagramon
a csillagok abszolút fényességének színképosztálytól való függése
van ábrázolva. Ez utóbbi arányos a felszíni hőmérséklettel. Ezen a
diagramon a csillagok jól meghatározott sávokban helyezkednek el.
Csak első közelítésben igaz, hogy a csillagok színképe a felszíni
hőmérsékletüktől függ, befolyásolja azt a fotoszférájuk sűrűsége,
amely viszont a felszíni gravitációs gyorsulással arányos. A nagy
luminozitású óriás csillagok felszíni gravitációs gyorsulása kisebb,
így légkörük ritkább, mint a fősorozati csillagoké. Így olyan spektrális
jegyek születnek, amelyek segítségével meg lehet különböztetni az
ugyanolyan színképosztályba tartozó, de más abszolút fényességű csillagokat.
Ezt módszert hívjuk spektroszkópiai parallaxisnak, hatótávolsága
kb. 2-5 kpc.
Russell-diagramon
a csillagok abszolút fényességének színképosztálytól való függése
van ábrázolva. Ez utóbbi arányos a felszíni hőmérséklettel. Ezen a
diagramon a csillagok jól meghatározott sávokban helyezkednek el.
Csak első közelítésben igaz, hogy a csillagok színképe a felszíni
hőmérsékletüktől függ, befolyásolja azt a fotoszférájuk sűrűsége,
amely viszont a felszíni gravitációs gyorsulással arányos. A nagy
luminozitású óriás csillagok felszíni gravitációs gyorsulása kisebb,
így légkörük ritkább, mint a fősorozati csillagoké. Így olyan spektrális
jegyek születnek, amelyek segítségével meg lehet különböztetni az
ugyanolyan színképosztályba tartozó, de más abszolút fényességű csillagokat.
Ezt módszert hívjuk spektroszkópiai parallaxisnak, hatótávolsága
kb. 2-5 kpc.
A spektroszkópiai parallaxis módszere mezőcsillagokra alkalmazva eléggé pontatlan eredményt ad. Éppen ezért a fotometriai távolságmeghatározás terén nagy jelentősege van a csillaghalmazoknak, mivel tagjaik tőlünk gyakorlatilag azonos távolságra vannak és így az egyes tagokra végzett mérések átlagolhatók.
A laza, szabálytalan alakú csillagcsoportokat nyílthalmazoknak nevezzük. Egy nyílthalmaz csillagai egymással szorosabb gravitációs kapcsolatban vannak, mint a mezőcsillagokkal. Ugyanez igaz az asszociációkra, viszont ezek azonos fajta csillagokat tartalmaznak. Távolságuk meghatározása a halmaz szín-fényesség diagramjának segítségével történik, amelyben a halmaz csillagjainak abszolút fényességét ábrázolják a színindexük függvényében.
Ha megfigyeljük egy halmaz csillagainak sajátmozgását, azt vehetjük
észre, hogy látszólag egy pont felé konvergálnak. Ez történhet egy
pont felé vagy egy pontból széttartóan. Ez hasonló egy madárcsoport
repüléséhez, amelyben a madarak párhuzamosan repülnek, látszólag mégis
egy irányba konvergálnak. Ha a halmaz elég nagy szögátmérőjű, akkor
a konvergens pont meghatározható. Ennek segítségével meghatározható
egy halmaz távolsága. Ezt a módszert konvergens pont módszernek
hívjuk. A módszer lényege a következő. Bontsuk fel a csillagok sebességét
látóirányú (![]() ) és arra merőleges (
) és arra merőleges (![]() ) komponensre! Jelöljük
) komponensre! Jelöljük
![]() -val a térbeli sebesség és a láróirányú sebességkomponens
szögét! Ekkor
-val a térbeli sebesség és a láróirányú sebességkomponens
szögét! Ekkor
| (12) |
![]() meghatározható a Doppler-eltolódásból,
meghatározható a Doppler-eltolódásból, ![]() -t mérjük.
Ebből a távolság:
-t mérjük.
Ebből a távolság:
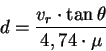 |
(13) |
Ebben az esetben a távolságot (d) pc-ben, a látóirányú sebességet
(![]() ) km/s-ban, a sajátmozgást (
) km/s-ban, a sajátmozgást (![]() )
)
![]() /év-ben
adjuk meg.
/év-ben
adjuk meg.
Másik módszer nyílthalmazok távolságának meghatározására az izokrón-illesztés.
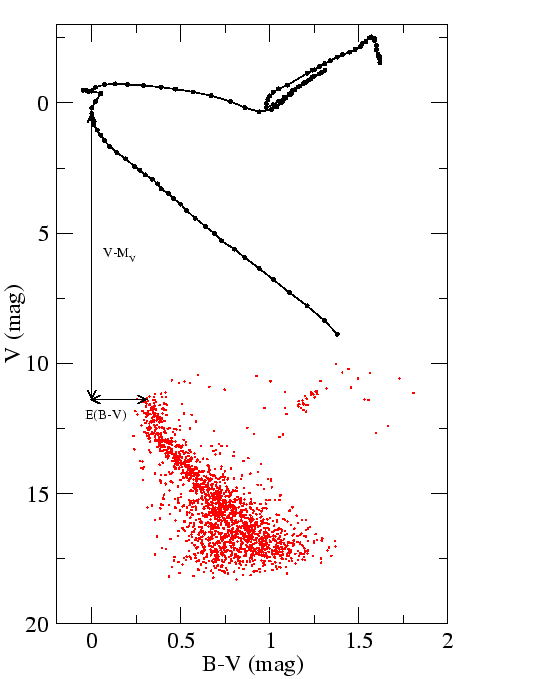
|
| (14) |
A megfigyelések szerint
| (15) |
Ezek segítségével adódik a távolság.