|
A Tejútrendszer szerkezetének meghatározásában alapvető fontosságú távolságmeghatározás rövid áttekintése után térjünk át a konkrét struktúra-meghatározás módszereire a megfigyelések tükrében.
Több módszer is létezik a csillagok és a gáz eloszlásának meghatározására. Az első módszer, amellyel kapott távolságot spektroszkópiai távolságnak hívunk, hogy ábrázoljuk az ismert csillagok távolságait. Ez egy közvetlen módszer a Tejútrendszer spirális szerkezetének meghatározására. Nagy hátránya ennek a módszernek, hogy a távolságok hibája kb. 10%, amely ahhoz vezet, hogy nagy bizonytalanságot visz a csillagok távolságába. Másik nagy hátránya, hogy kevés azoknak az objektumoknak a száma, amelyekre ez a módszer alkalmazható. Ilyen objektumok pl. az OB asszociációk, a nyílthalmazok, a legforróbb O csillagok, a HII területek, a 15 napnál hoszabb periódusú cefeidák. Az A és korai M színképtípusú csillagok is mutatnak némi sűrűsödést a karokban. Vannak olyan csillagok, amelyek szorosan, a spirálkarok mentén koncentrálódnak, ilyenek a Wolf-Rayet csillagok, a széncsillagok és a Be csillagok. Ezeket az objektumokat nevezzük a már említett spirálkar-indikátoroknak.
A távolságokat meg lehet határozni a spektrumvonalak sebességeiből, valamint a galaxis rotációs görbéjéből. Az így kapott távolságokat kinematikai távolságoknak hívjuk. Ezt a technikát a HI, HII és CO emissziós területeknél alkalmazzák. A Napon kívüli területeken a távolságok egyértelműek, de pontatlanok azért, mert pontatlan a rotációs görbe. A Napon belüli területeken minden egyes sebesség két lehetséges távolságnak felel meg, így ahhoz, hogy megkapjuk a távolságot, további információkra van szükség. Ennek a módszernek a hibája általában 10-20% körüli, mert az általános rotációs görbe nem ismert tökéletesen, az emissziós vonalak sebességei random szórást vihetnek a helyi általános sebességek környékén és a sugárzó gáz esetleges áramlásai a karok mentén vagy között ismeretlen sebességeket hozhatnak be.
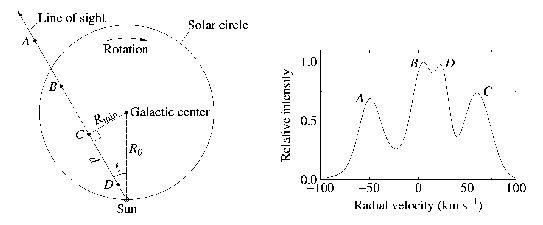
Szintén radiális sebességmérésen alapszik a tangenspont módszer. Egy adott galaktikus hosszúságban felvesszük a spektrumot (18. ábra).

|
| (16) |
A megfigyeléseken alapuló vizsgálatok kettő vagy négy, ritka esetben
három fő spirálkart eredményeznek, amelyek
![]() -os
szögben hajlanak. Galaxisunk spirálkarjainak hajlási szögének (p)
és számának (n) kérdésében eléggé megoszlanak a megfigyelési adatok,
viszont a logaritmikus spirál forma általánosan elfogadott. A négykarú
spirál a leginkább elfogadott. Mára már pontosabb távolságeloszlások
jellemzőek a HII területek mind optikai, mind rádiótartománybeli megfigyelési
adataira. Számos modern megfigyelési adat azt mutatja, hogy a mágneses
mező erővonalai az optikai tartományban párhuzamosak a spirálkarokkal,
így a mágneses erővonalak erősségének és irányának meghatározása a
spirálkarok meghatározását adja. A különféle módszerekkel különböző
eredmények adódnak.
-os
szögben hajlanak. Galaxisunk spirálkarjainak hajlási szögének (p)
és számának (n) kérdésében eléggé megoszlanak a megfigyelési adatok,
viszont a logaritmikus spirál forma általánosan elfogadott. A négykarú
spirál a leginkább elfogadott. Mára már pontosabb távolságeloszlások
jellemzőek a HII területek mind optikai, mind rádiótartománybeli megfigyelési
adataira. Számos modern megfigyelési adat azt mutatja, hogy a mágneses
mező erővonalai az optikai tartományban párhuzamosak a spirálkarokkal,
így a mágneses erővonalak erősségének és irányának meghatározása a
spirálkarok meghatározását adja. A különféle módszerekkel különböző
eredmények adódnak.
A por térbeli elhelyezkedésének optikai vizsgálatai meglehetősen nehezek, mivel az a galaktikus síkban koncentrálódik, így nem látunk túl messzire a korongban. Ezért azok a tanulmányok, amelyek ilyenfajta vizsgálaton alapulnak, eléggé pontatlanok.
A molekuláris CO és ![]() gázfelhők térbeli elhelyezkedésének vizsgálatai
már pontosabban mutatják a struktúrát. A hideg molekuláris CO rádiótartományban
tanulmányozható. Ahhoz, hogy ezek az adatok használhatóak legyenek,
kinematikai modell szükséges.
gázfelhők térbeli elhelyezkedésének vizsgálatai
már pontosabban mutatják a struktúrát. A hideg molekuláris CO rádiótartományban
tanulmányozható. Ahhoz, hogy ezek az adatok használhatóak legyenek,
kinematikai modell szükséges.
A meleg, atomos HI gáz tanulmányozása szintén rádiótartományú hullámhosszakon történik. Ehhez is szükséges kinematikai modell.
Az ionizált HII gáz térbeli elhelyezkedésének tanulmányozása optikai és rádiótartományban történik. Ezt gyakran használják fotometriai és kinematikai távolságmeghatározásra is.
A csillagok és csillaghalmazok tanulmányozása gyakran csak egyetlen távolságmeghatározási sémát használ, amely optikai fotometrián alapul. A galaktikus síkban lévő por miatt gyakran csak a legfényesebb csillagokra vannak korlátozva.
A spirálkarok modelljeként leggyakrabban a logaritmikus spirált használják
(19. ábra). A következő egyenlettel írható fel m számú karral
rendelkező spirálgalaxisra a karok intenzitásának hely és szögfüggése
(Vallée, 1995):
![\begin{displaymath}I(\theta,r)=A \cdot \cos{ \left[ 0,5 \cdot m \cdot \left\{ \t...
...t)^{-1} \cdot \ln {{r \over r_{0}}} \right) \right\} \right]}, \end{displaymath}](img144.png) |
(17) |
![\begin{displaymath}0,5 \cdot m \cdot \left[ \theta_{1}-\theta_{0}-\left\{ \left(...
...right)^{-1} \cdot \ln{{r_{1} \over r_{0}}} \right\} \right]=0, \end{displaymath}](img150.png) |
(18) |
![\begin{displaymath}0,5 \cdot m \cdot \left[ \theta_{1}+2\pi-\theta_{0}-\left\{ \...
...t)^{-1} \cdot \ln{{r_{1,next} \over r_{0}}} \right\} \right]=0 \end{displaymath}](img155.png) |
(19) |
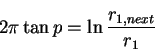 |
(20) |
Ha tekintjük az n-edik kart, ahol
![]() ,
maximális az intenzitás, ha
,
maximális az intenzitás, ha
![\begin{displaymath}0,5 \cdot m \cdot \left[ \theta-\theta_{0}-\left\{ \left(\tan...
...{{r_{n} \over r_{0}}} \right\} \right]=-\left( n-1 \right)\pi, \end{displaymath}](img159.png) |
(21) |
![\begin{displaymath}\theta-\theta_{0}=-2\pi\left( n-1 \right)m^{-1}+\left[ \left( \tan{p} \right)^{-1} \ln{{r_{n} \over r_{0}}} \right]. \end{displaymath}](img160.png) |
(22) |
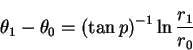 |
(23) |
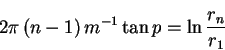 |
(24) |
Ugyanarra a karra ![]() szöggel később (n=m+1) a (24) egyenlet a
(20) egyenletre redukálódik. A második (n=2) és az első (n=1) kar
közti távolság s:
szöggel később (n=m+1) a (24) egyenlet a
(20) egyenletre redukálódik. A második (n=2) és az első (n=1) kar
közti távolság s:
| (25) |
| (26) |