Első példaként tegyük fel, hogy a csillag sűrűsége állandó, azaz
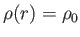 konstans.
Ekkor az r sugáron belüli tömeg egyszerűen
konstans.
Ekkor az r sugáron belüli tömeg egyszerűen
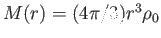 , tehát az
(1.7) egyenlet így írható:
, tehát az
(1.7) egyenlet így írható:
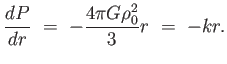 |
(1.18) |
ahol k konstans. Ez az egyenlet azonnal integrálható, megoldása:
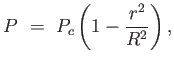 |
(1.19) |
amennyiben feltesszük, hogy a centrumban (r=0) a nyomás 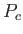 , a felszínen (r=R) pedig 0.
, a felszínen (r=R) pedig 0.
Szeged
2013-05-01