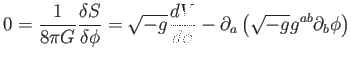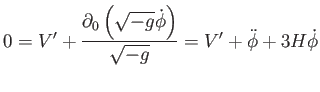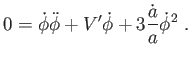Az infláció feltétele a gyorsuló tágulás, amely a Raychaudhuri-egyenlet értelmében
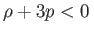 . Az Univerzum anyagát az inflaton dominálja, így a
hatásfüggvény:
. Az Univerzum anyagát az inflaton dominálja, így a
hatásfüggvény:
A hatásfüggvény 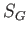 gravitációs részének (Einstein-Hilbert-hatás) a
funkcionális deriváltja éppen az Einstein-tenzor:
gravitációs részének (Einstein-Hilbert-hatás) a
funkcionális deriváltja éppen az Einstein-tenzor:
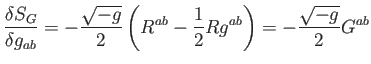 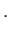 |
(6.30) |
Itt 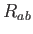 a Ricci-tenzor,
a Ricci-tenzor, 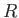 ennek a spúrja, a görbületi skalár és
ennek a spúrja, a görbületi skalár és 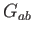 az Einstein-tenzor, míg
az Einstein-tenzor, míg 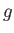 a metrikus tenzor determinánsa. Az első
egyenlőség levezetéséhez felhasználtuk a
a metrikus tenzor determinánsa. Az első
egyenlőség levezetéséhez felhasználtuk a
összefüggéseket. Az 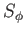 anyagi hatás
anyagi hatás 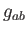 szerinti funkcionális
deriválja definíció szerint az energia-impulzus tenzor:
szerinti funkcionális
deriválja definíció szerint az energia-impulzus tenzor:
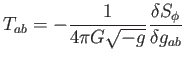 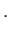 |
(6.33) |
A 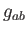 szerinti variálással így a (6.1) Einstein-egyenletekhez
jutunk.
szerinti variálással így a (6.1) Einstein-egyenletekhez
jutunk.
Az energia-impulzus tenzor pontos alakját a skalármezőt jellemző
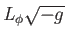 Lagrange-sűrűség határozza meg. Egy
Lagrange-sűrűség határozza meg. Egy 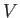 potenciáltérben
mozgó nemrelativisztikus részecske Lagrange-függvényének klasszikus térelméleti általánosítása:
potenciáltérben
mozgó nemrelativisztikus részecske Lagrange-függvényének klasszikus térelméleti általánosítása:
![$\displaystyle \mathit{L}_{\phi }=8\pi G\left[ \frac{1}{2}g^{ab}\partial _{a}\phi \partial _{b}\phi -V\left( \phi \right) \right] $](img1157.png) |
(6.34) |
a következő energiampulzus tenzorhoz vezet:6.6
![$\displaystyle T_{ab}=-g_{ab}\left[ \frac{1}{2}g^{cd}\partial _{c}\phi \partial _{d}\phi +V\left( \phi \right) \right] +\partial _{a}\phi \partial _{b}\phi$](img1160.png) 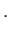 |
(6.35) |
FLRW-téridőben feltehetjük, hogy 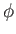 is homogén és izotrop, így csupán
az időnek függvénye. Ekkor
is homogén és izotrop, így csupán
az időnek függvénye. Ekkor 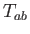 ideális folyadék típusúvá válik, amelyben
ideális folyadék típusúvá válik, amelyben
Az infláció feltétele
![$\displaystyle \rho +3p=2\left[ \dot{\phi}^{2}-V\left( \phi \right) \right] <0$](img1163.png) 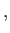 |
(6.37) |
vagyis
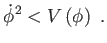 |
(6.38) |
A hatás 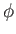 szerinti variálása a
szerinti variálása a
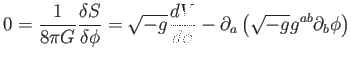 |
(6.39) |
Euler-Lagrange-egyenlethez vezet. Felhasználva hogy 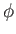 csak időtől függ, és
csak időtől függ, és
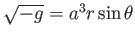 , valamint vesszővel jelölve a továbbiakban a
, valamint vesszővel jelölve a továbbiakban a 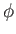 szerinti deriválást, a kapott Euler-Lagrange-egyenlet:
szerinti deriválást, a kapott Euler-Lagrange-egyenlet:
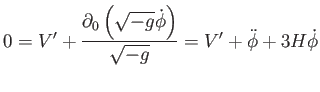 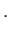 |
(6.40) |
Ez a súrlódási taggal (
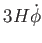 ) kiegészített Klein-Gordon-egyenlet
olyan speciális esete, amikor a
) kiegészített Klein-Gordon-egyenlet
olyan speciális esete, amikor a 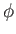 skalármező csak az időtől függ. A
gravitáció fejlődésegyenletei a Friedmann- és a Raychaudhuri-egyenletek, míg
a skalármezőé a súrlódással kiegészített Klein-Gordon-egyenlet.
skalármező csak az időtől függ. A
gravitáció fejlődésegyenletei a Friedmann- és a Raychaudhuri-egyenletek, míg
a skalármezőé a súrlódással kiegészített Klein-Gordon-egyenlet.
Végül megjegyezzük, hogy a skalármező energiasűrűségére és nyomására felírt
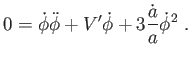 |
(6.41) |
folytonossági egyenlet ugyancsak megadja a skalármező fejlődésegyenletét,
amennyiben
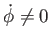 .
.
Szeged
2013-05-01
![]() . Az Univerzum anyagát az inflaton dominálja, így a
hatásfüggvény:
. Az Univerzum anyagát az inflaton dominálja, így a
hatásfüggvény: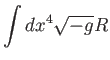
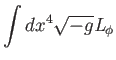
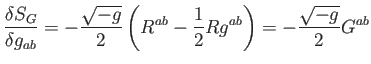
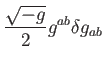
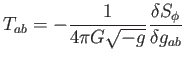
![]() Lagrange-sűrűség határozza meg. Egy
Lagrange-sűrűség határozza meg. Egy ![]() potenciáltérben
mozgó nemrelativisztikus részecske Lagrange-függvényének klasszikus térelméleti általánosítása:
potenciáltérben
mozgó nemrelativisztikus részecske Lagrange-függvényének klasszikus térelméleti általánosítása:
![$\displaystyle T_{ab}=-g_{ab}\left[ \frac{1}{2}g^{cd}\partial _{c}\phi \partial _{d}\phi +V\left( \phi \right) \right] +\partial _{a}\phi \partial _{b}\phi$](img1160.png)
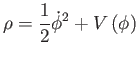
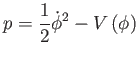
![$\displaystyle \rho +3p=2\left[ \dot{\phi}^{2}-V\left( \phi \right) \right] <0$](img1163.png)
![]() szerinti variálása a
szerinti variálása a