- ... teljesül5.1
- Az Einstein-féle összegzési konvenció értelmében a felül és alul egyaránt
megjelenő indexek összegzést jelentenek.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... is.5.2
- Általános esetben azonban az ideális
folyadék egyéb termodinamikai potenciáloktól is függ, mint a hőmérséklet,
barionszám-sűrűség, barionra eső entrópia és a barionok kémiai potenciálja.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... felvehet.5.3
- A
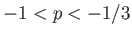 tartomány a kozmológiában használatos kvintesszecia
modellekhez vezet, a
tartomány a kozmológiában használatos kvintesszecia
modellekhez vezet, a 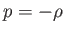 a legegyszerűbb sötét energia modellt, a
kozmológiai állandót írja le, végül a
a legegyszerűbb sötét energia modellt, a
kozmológiai állandót írja le, végül a  az ún. fantom energiaforma.
az ún. fantom energiaforma.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nő.5.4
- Kompakt csillagoknál
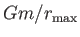 egységnyi nagyságrendű, míg közönséges
csillagoknál igen kicsi.
egységnyi nagyságrendű, míg közönséges
csillagoknál igen kicsi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... galaxisoknak5.5
- A Fanaroff és Riley által bevezetett FR I és FR II típusú rádióforrások közti határ
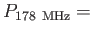
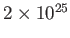 W Hz
W Hz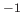 sr
sr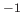 értéknél van.
értéknél van.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... folyadék6.1
- A folyadék négyessebessége a kozmológiai szimmetriáknak köszönhetően
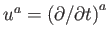 . Itt
. Itt 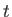 a folyadék sajátideje.
a folyadék sajátideje.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... értéke.6.2
- Általában a kozmológiában a nulla index a mennyiség jelenlegi értékét jelöli. A Hubble-paraméter
jelenlegi értékét Hubble-állandónak is nevezik.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... távoli6.3
- A távoli'' jelző
 -nél kisebb vöröseltolódású szupernóvákat jelöl. Ezek megfigyelési szempontból távol vannak, azonban
a kozmikus távolságokhoz képest eltörpülnek ezek a távolságok, így lényegében csak a nagyon késői Univerzum szupernóva-robbanásairól vannak adataink.
-nél kisebb vöröseltolódású szupernóvákat jelöl. Ezek megfigyelési szempontból távol vannak, azonban
a kozmikus távolságokhoz képest eltörpülnek ezek a távolságok, így lényegében csak a nagyon késői Univerzum szupernóva-robbanásairól vannak adataink.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... modell6.4
- A
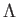 kozmológiai állandó és a hideg sötét anyag (Cold Dark
Matter = CDM) fő komponensekből álló Univerzum-modell.
kozmológiai állandó és a hideg sötét anyag (Cold Dark
Matter = CDM) fő komponensekből álló Univerzum-modell.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... hőmérséklettől6.5
- A Boltzmann-konstans egységnyinek választása azt jelenti, hogy a hőmérséklet
és az energia dimenziója megegyezik, a kelvin és az elektronvolt közötti váltószám pedig:
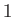 K
K
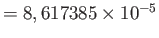 eV.
eV.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... vezet:6.6
- Megjegyezzük, hogy a (6.34) skalármező Lagrange-sűrűségében a
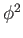 dimenziója a
dimenziója a 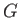 gravitációs állandó inverzének dimenziójával egyezik, ez a gravitációs
gravitációs állandó inverzének dimenziójával egyezik, ez a gravitációs
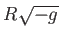 Lagrange-sűrűséggel való összevetésből látszik.
Lagrange-sűrűséggel való összevetésből látszik.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... során.6.7
- A kozmikus mikrohullámú háttérsugárzás anizotrópiáinak kialakulásában fontos
szerepet játszik a kozmikus fotonok rekombináció alatt végbemenő szabad
elektronokon történő Compton-szóródása. Ezért a foton hőmérsékleti fluktuációinak elméleti származtatásához szükséges a szabad elektronok számsűrűsége időfejlődésének ismerete. A hidrogén- és
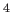 He atommagokon túlmenően a
nukleszintézis során keletkezett (
He atommagokon túlmenően a
nukleszintézis során keletkezett (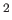 H,
H, 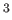 He, Li, ...) könnyű
atommagoknak a rekombinációhoz adott járuléka csak mintegy
He, Li, ...) könnyű
atommagoknak a rekombinációhoz adott járuléka csak mintegy 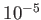 rendű
korrekciót okoz a kozmikus mikrohullámú háttérsugárzás teljesítményspektrumában [22].
rendű
korrekciót okoz a kozmikus mikrohullámú háttérsugárzás teljesítményspektrumában [22].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mértékben6.8
- A háttér-téridőn az
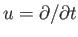 vektormező integrálgörbe-serege
nyírásmentes. Newtoni mértékben az
vektormező integrálgörbe-serege
nyírásmentes. Newtoni mértékben az 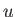 görbeseregnek megfelelő perturbált görbeseregnek nincs skalárperturbációkból származó nyírása (lehet azonban
tenzor-perturbációkból származó nyírása).
görbeseregnek megfelelő perturbált görbeseregnek nincs skalárperturbációkból származó nyírása (lehet azonban
tenzor-perturbációkból származó nyírása).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
szerinti6.9
- Az
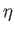 bevezetésével a Friedmann-téridő csak egy konformis szorzóban különbözik a Minkowski-téridőtől. A konformis szorzó a skálafaktor négyzete.
bevezetésével a Friedmann-téridő csak egy konformis szorzóban különbözik a Minkowski-téridőtől. A konformis szorzó a skálafaktor négyzete.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Durrer:6.10
-
Megjegyezzük, hogy az itt használt
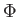 Bardeen-potenciál előjelben különbözik [26] azonos jelű potenciáljától.
Bardeen-potenciál előjelben különbözik [26] azonos jelű potenciáljától.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... korszakban.6.11
- Ezt azt eredményezi, hogy pordominált korszakban nincs integrális
Sachs-Wolfe-effektus, az ugyanis a Bardeen-potenciálok időderiváltjáival áll kapcsolatban.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... konstans.6.12
- Megjegyezzük azonban, hogy bizonyos perturbációkkal kapcsolatos eredmények származtatásához a
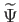 ,
,
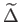 és
és
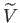 mennyiségeket
mennyiségeket
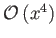 rendben kell megadni.
rendben kell megadni.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...-erdő6.13
- A semleges hidrogént tartalmazó intergalaktikus anyagfelhők abszorpciós
detektálására szolgáló módszer.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
seffektusait6.14
- Anizotrop sugárzás a Compton-szórás következtében lineárisan polarizálttá válik, mert a Thomson-hatáskeresztmetszet függ a
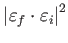 szögtől, ahol
szögtől, ahol
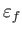 és
és
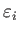 a végső és a kezdeti polarizációs vektorok. Átlagolva a beeső
és felösszegezve a végső polarizációs állapotokra, a szögfüggés
a végső és a kezdeti polarizációs vektorok. Átlagolva a beeső
és felösszegezve a végső polarizációs állapotokra, a szögfüggés
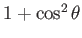 , ahol
, ahol 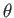 a szóródó foton kezdeti és végső impulzusa közti szög. A lineárisan polarizált sugárzás szórása ettől eltérő szögfüggésű
lehet. Ez hatással van hőmérsékleti perturbációkat leíró Boltzmann-egyenlet
szórási tagjára. A polarizáció hatása a hőmérsékleti
a szóródó foton kezdeti és végső impulzusa közti szög. A lineárisan polarizált sugárzás szórása ettől eltérő szögfüggésű
lehet. Ez hatással van hőmérsékleti perturbációkat leíró Boltzmann-egyenlet
szórási tagjára. A polarizáció hatása a hőmérsékleti 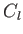 spektrumra
spektrumra 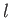 növekedésével nő. Elhanyagolása az első csúcs helyzeténél (
növekedésével nő. Elhanyagolása az első csúcs helyzeténél (
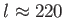 )
) 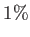 -os,
-os,
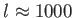 -nél körülbelül
-nél körülbelül  -os hibát eredményez [22].
-os hibát eredményez [22].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... szög-teljesítményspektrum6.15
- A matematikai statisztikában a (6.130) függvényt 2-pont-kovarianciának nevezik. A statisztikai homogenitás és izotrópia miatt (6.130)
csak konstanstban tér el a statisztikában használatos 2-pont-korrelációs függvénytől.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
:6.16
- Megjegyezzük, hogy a Fourier-transzformáció itt használt integrálási mértéke
eltér [37] irodalométól. Az itt használt mérték a
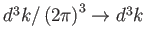 reláción keresztül kapcsolódik [37]-éhez. A (6.134) összefüggésben a konformis időre tértünk át.
reláción keresztül kapcsolódik [37]-éhez. A (6.134) összefüggésben a konformis időre tértünk át.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... görbületétől.6.17
- Mivel az egyszerűség kedvéért a
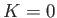 Univerzum perturbációit tárgyaltuk
eddig, egyenleteinkből explicite nem látszik, hogy hol jelenne meg a
Univerzum perturbációit tárgyaltuk
eddig, egyenleteinkből explicite nem látszik, hogy hol jelenne meg a 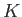 -függés. Azonban a perturbációkat vizsgálták tetszőleges
-függés. Azonban a perturbációkat vizsgálták tetszőleges 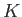 esetén is. Ilyenkor
is létezik harmonikus kifejtés, ahol a bázisfüggvények az adott görbületű tér Laplace-Beltrami-egyenletének megoldásai.
esetén is. Ilyenkor
is létezik harmonikus kifejtés, ahol a bázisfüggvények az adott görbületű tér Laplace-Beltrami-egyenletének megoldásai.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.