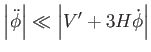A lassú gördülés modellje

Lassú gördülés akkor áll fenn, ha a skalármező változási sebességének négyzete kicsi a potenciálhoz képest, vagyis

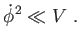$$\dot{\phi}^{2}\ll V .$$ (6.42)

Ekkor 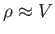 $\rho \approx V$ és a Friedmann-egyenlet

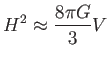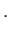$$H^{2}\approx \frac{8\pi G}{3}V .$$ (6.43)

Lassú gördüléskor továbbá 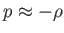$p\approx -\rho$, ami a kozmológiai konstans állapotegyenlete. A folytonossági egyenletből ekkor 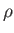$\rho$ közel állandó, így a Friedmann-egyenlet miatt 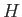$H$ is. Már láttuk, hogy ilyenkor a kozmológiai fejlődés exponenciális táguláshoz vezet.

A lassú gördülés másik,

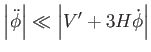$$\left\vert \ddot{\phi}\right\vert \ll \left\vert V^{\prime }+3H\dot{\phi} \right\vert$$ (6.44)

feltételének értelmében a skalármező egyenlete

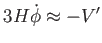$$3H\dot{\phi}\approx -V^{\prime }$$ (6.45)

alakra egyszerűsödik.