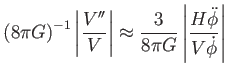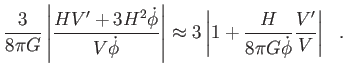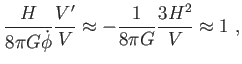Vezessük be az alábbi (dimenziótlan) paramétereket:
A következőkben belátjuk, hogy a lassú gördüléses inflációhoz szükséges,
hogy mind
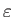 , mind
, mind 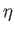 kicsi legyen.
kicsi legyen.
A (6.45) egyenlet négyzetét elosztva a (6.43) egyenlet 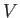 -szeresével kapjuk, hogy
-szeresével kapjuk, hogy
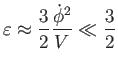  |
(6.47) |
A Friedmann- és Raychaudhuri-egyenletek különbségét képezve (6.38) közelítésben kapjuk, hogy
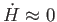 , tehát
, tehát 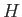 közelítőleg állandó
a lassú gördülés közben. Ezt felhasználva, (6.45) időderiváltja adja, hogy:
közelítőleg állandó
a lassú gördülés közben. Ezt felhasználva, (6.45) időderiváltja adja, hogy:
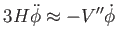 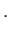 |
(6.48) |
Amiből következik, hogy:
A (6.45) egyenlet értelmében viszont
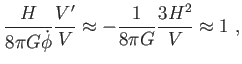 |
(6.50) |
így
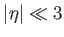 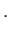 |
(6.51) |
Szeged
2013-05-01
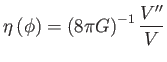
![]() -szeresével kapjuk, hogy
-szeresével kapjuk, hogy
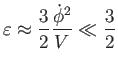
![]() , tehát
, tehát ![]() közelítőleg állandó
a lassú gördülés közben. Ezt felhasználva, (6.45) időderiváltja adja, hogy:
közelítőleg állandó
a lassú gördülés közben. Ezt felhasználva, (6.45) időderiváltja adja, hogy: