A hatáskeresztmetszet becslése

A magreakció hatáskeresztmetszete a reakciók valószínűségével arányos mennyiség. Értéke főként két mennyiségtől függ: a magok klasszikus ütközési valószínűségét megadó ütközési hatáskeresztmetszettől és a Coulomb-gáton történő átjutáshoz szükséges alagúteffektus valószínűségétől.

A klasszikus ütközési hatáskeresztmetszet ($\sigma_u$) a gömb alakú magok körnek látszó területével arányos. Mivel a reakcióhoz szükséges ütközési távolság a de Broglie-hullámhosszhoz közeli, (1.47) értelmében $\sigma_u \sim \pi \lambda_B^2 = \pi (h / p)^2 \sim 1/E$, ahol E a bombázó részecske kinetikus energiája.

Az alagutazás valószínűsége (1.48) alapján $\sigma_a \sim \exp(-b / \sqrt{E})$, ahol $b = Z_1 Z_2 e^2 \sqrt{2m} / h$.

A fenti két formula szorzata adja a magreakció teljes hatáskeresztmetszetét:

$$\sigma(E) =  S(E) \cdot {1 \over E} \exp [-b E^{-1/2} ] ,$$ (1.55)

ahol S(E) jelöli a fenti képletekben nem szereplő további effektusok energiafüggését. A sebességre átlagolt hatáskeresztmetszetet ezek alapján az alábbi kifejezésből kaphatjuk:

$$\langle \sigma v \rangle =  \int_0^\infty \sigma(E)\cdot v(e) \cdot f(E) dE.$$ (1.56)

Ha a magok sebességeloszlására a Maxwell-Boltzmann-eloszlásfüggvényt használjuk,

$$f(E) =  {2 \over \sqrt{\pi}} {E^{1/2} \over {kT^{3/2}}} \exp [-E/(kT)]$$ (1.57)

és figyelembe vesszük, hogy nemrelativisztikus részecskékre $v(E) = \sqrt{2E / m}$, kaphatjuk:

$$\langle \sigma v \rangle =  \sqrt{\frac{8}{m\pi}} (kT)^{-3/2} \int_0^\infty S(E) \exp \left [ - {E \over {kT}} - {b \over \sqrt{E}} \right ] dE$$ (1.58)

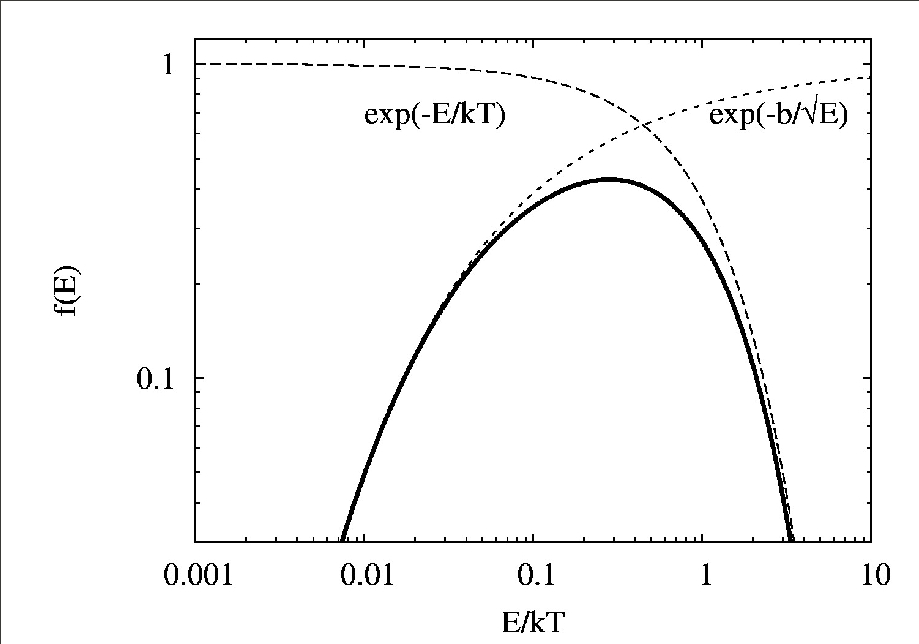
Az exp[...] függvény grafikonját az 1.4. ábra mutatja. Látható, hogy növekvő E-re az első tag csökkenő, míg a második növekvő hozzájárulást ad. A kettő szorzata egy haranggörbét ad, ez a Gamow-csúcs. A Gamow-csúcs maximumhelye az $E_0 = (b k T/2)^{2/3}$ energiánál van, ezen a helyen a maximum értéke $g(E_0) = \exp[-3 E_0 / (kT)]$.

1.4. Ábra: A magreakció hatáskeresztmetszetét (vastag vonal) a Maxwell-Boltzmann eloszlás (szaggatott vonal) és az alagúteffektus (pontozott vonal) valószínűségének szorzata adja (részletes magyarázat a szövegben).