Rezonáns hatáskeresztmetszet

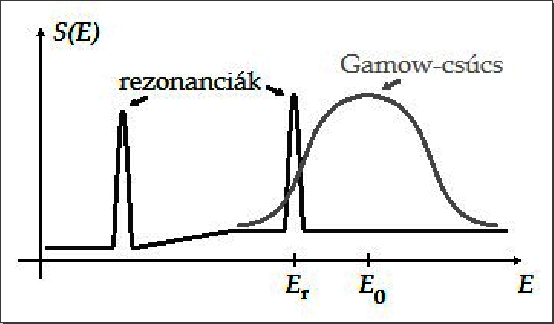
Az előzőtől lényegesen különböző esetben a Gamow-csúcs körül S(E) nagyon éles, keskeny és magas csúcsokat mutat (1.5. ábra). Az ilyen jellegű reakciónak rezonáns hatáskeresztmetszete lesz. A rezonancia energiája legyen $E_r$. Ekkor $S(E) \approx S(E_r)$, ha $E_r - \Gamma / 2 < E < E_r + \Gamma/2$, ahol $\Gamma$ a rezonanciacsúcs szélessége, ezen kívül $S(E) \approx 0$.

Mivel a rezonancia $\Gamma$ szélessége általában sokkal kisebb, mint a Gamow-csúcs félértékszélessége, ebben az esetben (1.58) integrandusa egy lépcsős függvénnyel közelíthető, amely $\Gamma$ szélességű, magassága pedig az integrandus $E_r$ helyen felvett értéke. Ez azonnal integrálható, így a rezonáns hatáskeresztmetszetre a következő kifejezést kapjuk:

$$<\sigma v>_{r} =  \sqrt{8 \over {m \pi}} (kT)^{-3/2} \cdot S(E_r... ...t \Gamma \cdot \exp \left [ -{E_r \over {kT}} - {b \over \sqrt{E_r}} \right ] .$$ (1.61)

A hőmérsékletfüggést explicite kifejezve az alábbi összefüggés adódik:

$$\langle \sigma v \rangle_{r} =  \langle \sigma v \rangle_{r}(0) \cdot T^{-3/2} \cdot \exp [-a_2 E_r / T].$$ (1.62)

Az (1.60) képlettel összevetve látható, hogy a rezonáns hatáskeresztmetszet sokkal erősebben függ a hőmérséklettől, mint a nemrezonáns.

A magreakciók különféle energiákon különbözőek lehetnek. Így gyakran előfordul, hogy két mag ütközése bizonyos energiákon nemrezonáns, más energiákon rezonáns kölcsönhatást eredményez. A teljes hatáskeresztmetszet általában (1.59) és (1.61) alakú függvények szuperpozíciójával adható meg (lásd 1.5. ábra).

1.5. Ábra: A teljes hatáskeresztmetszet a rezonáns és nemrezonáns hatáskeresztmetszetek szuperpozíciójaként állítható elő.