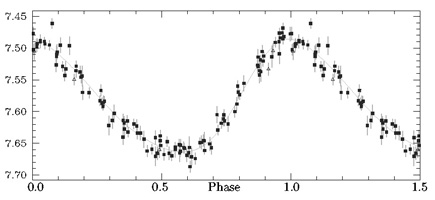
IV.1. V2109 Cygni

IV.1.1. Fotometriai analízis

   A V2109 Cygni (= HD191635 = SAO49242 = HIP99252, F0 színképtípus) változócsillagot az 1989 és 1993 között földkörüli pályán asztrometriai méréseket végző Hipparcos műhold fedezte fel (ESA, 1997). Fénygörbéje alapján rövid periódusú (P=0,1860656 nap), viszonylag kisamplitúdójú (V=7.48-7.67) RRc típusú csillagnak katalogizálták. A dolgozat elején már említettem, hogy a fénygörbe alakján alapuló típusmeghatározás elég bizonytalan módszer. A műhold méréseiből elkészített fénygörbe (l. 5. ábra) és a fent említett paraméterek ugyanúgy tartozhatnak egy rövid periódusú RR Lyrae és egy hosszú periódusú, nagy amplitúdójú d Scuti csillaghoz is (l. pl. Rodríguez et al. 1998).

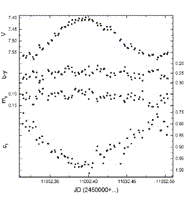
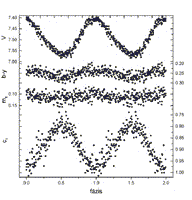
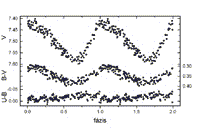
1998 nyarán és őszén összesen öt éjszakán mértük a csillagot; uvby szűrőkön keresztül: augusztus 6-án, 11-én, szeptember 23-án; UBV szűrőkön át: szeptember 30-án és október 23-án. Összehasonlítóként minden esetben a HD191022 jelű csillagot (V=7.44, G0) használtuk. Példaképpen bemutatjuk az augusztus 6-ai mérést a 6. ábrán, míg az összes mérésből kapott fázisdiagramok a 7. és 8. ábrán láthatók.

IV.1.2. A periódus vizsgálata

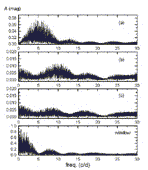
   A fotometriai periódust Fourier-analízis és O-C diagram segítségével vizsgáltuk. Az összes V-szűrős mérésből származó fénygörbén diszkrét Fourier-transzformációt (DFT) hajtottunk végre. A DFT-spektrumban egyetlen domináns csúcs található (9. ábra) az f₀=5,37488 ciklus/nap (P=0,18605 nap) értéknél, ami jól egyezik a Hipparcos-periódussal (0,1860656 nap).     Ezen frekvencia és harmonikusainak levonása után a periodogram egyetlen jelentős csúcsot sem tartalmaz, ami azt sugallja, hogy a V2109 Cyg monoperiodikus fénygörbéjű, azaz egyetlen módusban pulzál.
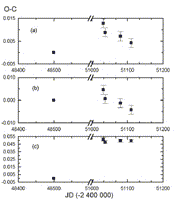
   A V-fénygörbékből négy új maximumidőpontot sikerült meghatároznunk (l. 8. táblázat), melyeket felhasználva a periódus értékének finomításához O-C diagramot használtunk. A 10.a ábra az eredeti, Hipparcos-fotometriából származó efemeris (E₀=2448500.280, P=0.1860656 nap) felhasználásával készült. Az ábrán jól látható pozitív ugrás mutatja, hogy a jelenlegi periódus valamivel hosszabb, mint az eredeti efemerisbeli érték. A 10.b ábra mutatja az előző ábra alapján újraszámolt O-C értékeket. Mindkét ábrán jól láthatóan csökkennek a méréseinkből származó O-C értékek, ami viszont rövidebb periódusra utal. Az erre korrigált új O-C diagram a 10.c ábrán látható (P=0,1860495 nap).
 

IV.1.3. A vörösödés meghatározása

   A fotometriai vizsgálatok előtt egy igen fontos korrekciót kell végrehajtani, amely a csillagközi por vörösítő hatását veszi figyelembe. A köznapi életben is tapasztalt (például egy szép naplemente végignézése közben) jelenség a Nap „vörösödése", aminek hátterében az áll, hogy a légkörben lebegő porszemcsék kiszórják a Nap fényének kék összetevőjét. Hasonló hatással van a csillagközi anyag a csillagok megfigyelhető fényére és színére is. A többszín-fotometriai rendszerekben ez a jelenség a színindexek változásában mutatkozik (amellett, hogy a csillag fénye gyengül), ami pedig hamis eredményekhez vezet. A csillagközi pornak ezt, a színindexekre gyakorolt hatását vörösödésnek nevezzük.
   A Johnson-féle rendszerben a színindexek változásával jellemezzük a vörösödést, míg a megfigyelt és a „tiszta" színindexek különbségét színexcesszusnak nevezzük. A szokásos jelölések az egyes színindexekre E(U-B) és E(B-V); ugynez formulákba öntve (Henden & Kaitchuk, 1990):

                                (38)
  ,                                 (39)

                                (40)

                                               (41)

                                                (42)
  .                                             (43)

  .                                             (44)

   A V2109 Cygni átlagos B-V értéke méréseimből: <B-V>=0,35±0.01. Carroll & Ostlie (1996) művében található, óriáscsillagokra vonatkozó táblázatból F0 színképtípusú csillagra a „tiszta" B-V értéke: (B-V)_i=0,30. Mindezekből E(B-V)=0,05±0.03. A viszonylag nagy bizonytalanság abból ered, hogy a színképtípust bizonytalansága legalább ±2 altípus.
   Mindemellett két Strömgren kalibrációt is felhasználtunk a tiszta (b-y)₀ színindex meghatározásához. Crawford (1975) és Olsen (1988) közölt uvby-b kalibrációt F színképtípusú csillagokra. Mivel nekünk nem állt rendelkezésünkre b-mérés, ezért a b index értékeit Strömgren indexek - b diagramokból határoztuk meg (Crawford 1975, 1.,3.,6. ábra). Végeredményül a b=2,70±0,02 értéket kaptuk. Ezen értéket behelyettesítve Crawford (1975) és Olsen (1988) végső kalibrációs képleteibe E(B-V)=0,00 és E(B-V)=-0,02 értékek álltak elő. Az előzőekben kiszámított vörösödésekből E(B-V) átlagos értéke 0,006, azonban a b index bizonytalan meghatározása miatt az egyszerű átlag helyett a spektráltípus-színindex összefüggéshez nagyobb súlyt rendelve a három vörösödés súlyozott átlaga (3-1-1 súlyokkal) E(B-V)=0,03±0,02. Ezt fogadtuk el, és használtuk a további analízis során.
   A Strömgren-rendszer színexcesszusaira a következő összefüggések érvényesek (a részletekre vonatkozóan l. Budding, 1993):

                                            (45)
                                               (46)
                                             (47)

 IV.1.4. Az effektív hőmérséklet és felszíni gravitációs gyorsulás meghatározása

   A T_eff és log g  meghatározásához Kurucz (1993) elméleti csillaglégkör-modelljeit használtuk fel. A modellek három fő paramétert tartalmaznak: különböző fémtartalom ([Fe/H]) mellett a T_eff és log g értékek rögzített közű léptetésével sikerült lefedni a valós csillagokra jellemző paraméter-tartományokat. Kurucz számításaiban a modellcsillagok fluxusát határozza meg, majd ezt a fotometriai rendszerek szűrőfüggvényeivel konvolálva szintetikus színindexeket származtat. A megfigyeléseket ezekkel hasonlítjuk össze, majd a modellcsillagokat megfeleltetjük a valóságnak. Természetesen az a megközelítés is terhelt bizonyos problémákkal, pl. Kurucz sztatikus csillagatmoszférákkal dolgozik, míg a pulzáló változók légköre folyamatos mozgásban van, ami némileg meghamisítja az eredményeket. Kis amplitúdójú változásoknál viszont (mint pl. a V2109 Cyg esetében) jó közelítésként feltehetjük, hogy a csillag kvázisztatikus állapotokat jár be a pulzációja során.
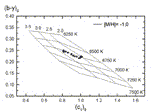
   T_eff és log g meghatározása a fotometriai mérésekből szín-szín diagramok segítségével történik. A csillag egyes pulzációs fázisaihoz tartozó, fotometriai mérésekből származó és vörösödésre korrigált színindexértékeket felrajzoljuk a (b-y)-c₁ diagramra, majd rávetítjük az elméleti modellből származó T_eff-log g hálót. Az egyes pulzációs fázisokhoz tartozó T_eff és log g értékeket kétdimenziós lineáris interpolációval kapjuk meg (l. 11. ábra).
   Az említett szín-szín diagram használatát a (b-y)-m₁ diagram ellenében két tényező is indokolja. Egyrészt a c₁ görbe amplitúdója sokkal nagyobb, mint az m₁ esetében, azaz, a fotometriai hibák hatása jóval kisebb. Másrészt a (b-y)-c₁ sík elméleti hálói viszonylag érzéketlenek a modellek fémtartalmára. Így a [Fe/H] aktuális értékétől csak gyengén fog függeni a kapott hőmérséklet és felszíni gravitációs gyorsulás. A csillag fémtartalmát a b-y, m₁ és c₁ színindexek átlagos értékeiből, Malyuto (1994) (2)-es egyenletének felhasználásával határoztuk meg. Eredményül a [Fe/H]=-0.9±0,2 értéket kaptuk, ami jó összhangban áll az RR Lyrae típus jellemző értékével ([Fe/H]=-1,0). A lineáris interpoláció elvégzése után a V2109 Cyg hőmérséklete átlagosan <T_eff>=6800±200 K; míg gravitációs gyorsulása <log g>=2,7±0.2.
 

IV.1.5. Spektroszkópia

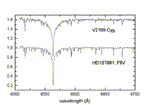
   A V2109 Cygniről október 19-én és 21-én készültek színképfelvételek a DDO-ban. Standard sebességcsillagként a HD187691(= 54 Aql = SAO105338 = HIP97675) jelű, F8V színképtípusú csillagot használtuk, melynek heliocentrikus sebessége +0,1 km/s. A felvételek korrigálásait (bias és flat korrekció, kozmikussugár eltávolítás) és a kiértékelést az IRAF képfeldolgozó programcsomaggal végeztük. A 12. ábrán a HD187691 és a V2109 Cyg kontinuum-normált spektruma látható.
 

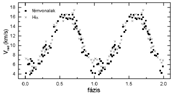
A V2019 Cyg radiális sebesség-változását keresztkorrelációs módszerrel határoztuk meg. Az eljárást külön elvégeztük a H-a-vonalra és a fémvonalakra. Az eredményül kapott, a Föld mozgására korrigált radiális sebesség görbe a 13. ábrán látható. A kétféle sebesség közötti különbségek nem haladják meg magát a mérés hibáját, ami arra utal, hogy a V2109 Cyg légkörében a pulzáció nem okoz kimutatható sebesség-gradienst. II-es típusú cefeidákban a pulzáció sorábn fellépő lökéshullámok, illetve a csillaglégkör nagy kiterjedése miatt akár több 10 km/s-os sebességkülönbség is felléphet bizonyos fázisokban (Vinkó et al. 1998). I-es típusú cefeidákban már sokkal nyugodtabb lefolyású a rezgés, bár kimutatható néhány km/s-os eltérés az adatokban (Kiss 1998). Az RRab csillagokban szintén jól ismert a fáziskésés az atmoszféra átlagosan mélyebb rétegeiben keletkező fémvonalak és a magasabbról származó hidrogénvonalak sebessége között (Van Hoof effektus - Mathias & Gillet 1993). Ehhez képest a V2109 Cyg pulzációja nélkülözi a durva lökéshullámokat és a csillaglégkör egyszerre végzi a táguló, majd összehúzódó mozgást.
 

IV.1.6. Asztrofizikai paraméterek - sugár, tömeg, luminozitás

   A Hipparcos asztrometriai műhold nagy pontossággú csillagparallaxis-méréseket is végzett, azaz ismert a csillag távolsága. A V2109 Cygni parallaxisa (ESA, 1997): p= 4,9±0,9 mas (ezred ívmásodperc), aminek reciproka megadja a távolságot parszekben. Így a V2109 Cyg távolsága: d=205±41 parszek.
   Ismerve a csillag távolágát és látszólagos fényességet, megkaphatjuk az alábbi képlet szerint az abszolút fényességét is:

  ,                        (48)

  ,                                     (49)

  ,                        (50)

  ,                            (51)

IV.1.7. Fourier-analízis - második felhangú pulzáció?

   A 14. ábrán a GCVS-ben található RR Lyrae csillagok adataiból készült hisztogram látható. A vízsintes tengelyen a periódusidő, a függőleges tengelyen a gyakoriság van feltüntetve.
 

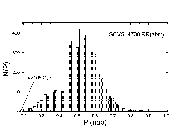
   A hisztogramon két feltűnő csúcs látható: a rövidebb periódusú RRc-k, és hosszabb periódusidejű RRab-k jellemző periódusidejénél. A V2109 Cyg messze a legrövidebb periódusidejű a katalógusbeli RR Lyrae-k között. P=0,23 napnál egy erős levágást tapasztalunk, azaz, ennél rövidebb periódusok nem fordulnak elő. Az általánosan elfogadott magyarázat szerint az RRab csillagokban a fundamentális mód van jelen, míg az RRc csillagok az első felhangban végzik pulzációjukat. Az irodalomban a legutóbbi időkig ellentmondásos munkák jelentek meg a második felhang lehetséges gerjesztettségéről. Egyes gömbhalmazok (pl. M68) RR Lyrae csillagai között előfordulnak olyan rövidperiódusú (0,22-0,23 nap) RRc csillagok, melyek az ugyanazon halmaz átlagos RRc-periódusának 0,8-szorosával változtatják fényességüket (pl. Walker 1994). Ez az érték az elméleti számítások szerint éppen az első és a második felhang periódusának az aránya. Mások számításai szerint (Kovács 1997, 1998) ezek csak extrém rövid periódusú, első felhangú pulzátorok. A V2109 Cygni periódusidejét elosztva 0,8-cal P=0,23 nap értéket kapunk, ami utalhat arra, hogy a V2109 Cygni a második felhangban pulzál. Ez azonban ennél a pontnál puszta spekuláció, részletesebben a fénygörbe és radiális sebesség görbe Fourier-analízise szolgálhat információval.

IV.1.8. A fénygörbe és radiális sebesség görbe analízise

   A hullámtanból ismert, hogy minden periodikus folyamat előállítható megfelelő amplitúdójú és fázisú szinuszos rezgések eredőjeként. A fénygörbét és a radiálissebesség-görbét megadhatjuk az

                           (52)

   ,                                     (53)

 sugallja, hogy a pulzációja második felhangban történik. Ezen következtetés alapvető fontossággal bír, ugyanis a pulzáló változócsillagok talán legfontosabb jellemzője a pulzáció módusa. A megfigyelhető változások pontos értelmezése csak akkor válik lehetővé, ha teljes leírást adhatunk - a kérdést jól illusztrálják pl. a különböző módusban pulzáló klasszikus cefeidák, melyeknél az egyetlen megfigyelhető periódust felhasználva, ill. különböző módusokat feltételezve többszörös faktorral különböző luminozitást, sugarat, tömeget, stb. kaphatunk.     Mint már említettük, az RRab és RRc típusú RR Lyrae-k különbségeit úgy értelmezhetjük, hogy alapmódusban és első felhangban pulzálnak. A második felhangban rezgő RR Lyrae-k (RRe) kérdése ellentmondásos eredményeket szolgáltatott az elmúlt 20-25 évben. Egyes gömbhalmazok RR Lyrae populációjának rövid periódusú tagjai mellett (Walker & Nemec 1996) a MACHO mikrolencse-program fotometriai melléktermékei között is szerepelnek RRe-jelölt csillagok (Alcock et al. 1996). Kovács (1997, 1998) elméleti megfontolások alapján elveti a lehetőséget, mivel modellszámításai szerint a megfigyelt 0,23-0,28 nap periódusok túl hosszúak a feltételezett RRe állapothoz.
   A V2109 Cyg periódusa, fizikai jellemzői, fény- és radiális sebesség görbe paraméterei egyaránt összhangban vannak a második felhang feltételezésével, illetve Kovács (1997, 1998) elméleti számításaival. Ennek olyan érdekes következménye is van, hogy a csillag belsejében két csomófelület is van, amelyek között rezgés történik. A pulzációs modellek oldaláról közelítve is társítható elméleti jelentőség ezen speciális rezgésállapothoz. Az eddigi modellek jóslatai tagadták a második felhang stabil jellegét. A V2109 Cyg fényében a modellek legfontosabb belső paraméterei, melyek a csillagszerkezetre, sugárzásterjedés leírására, stb. vonatkoznak, legalább is egy részletes átgondolásra szorulnak.

 IV.2. DX Ceti

   A DX Ceti (= NSV 00871 = HIP 12113 = HD 16189, <V>= 7.00, DV= 0.2, P=0,1039 nap, A5 színképtípus) fényváltozását először Stetson (1991) mutatta ki fotoelektromos mérésekkel, de nem mérte ki a teljes fénygörbét. Monoperiodikus természetét a Hipparcos műhold fedezte fel (17. ábra, ESA 1997), és RRc típusú változócsillagként katalogizálták. Vagyis a DX Ceti lenne

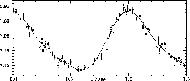
a legrövidebb periódusidejű az összes ismert RR Lyrae csillag között. Ez a kijelentés azonban meglehetősen ingatag alapokon áll, ha nem ismerjük a csillag fizikai paramétereit.
   A csillagról kérésünkre 1998. november 17-én színképfelvételek készültek a torontoi David Dunlap Observatory 1,88 m-es távcsövére szerelt Cassegrain spektrográffal. Standard sebességcsillagként ekkor is a HD 187691 jelű csillagot használtuk. A színképfelvételek korrigálását és a kiértékelést az IRAF képfeldolgozó programcsomaggal végeztük. A DX Cet radiálissebesség-változástát keresztkorrelációs módszerrel határoztuk meg a színkép 6550-6700 Å közé eső tartományán.
   A kedvezőtlen időjárás és a rossz szegedi asztroklíma ellenére 1998. november 18-án sikerült mérni a csillagot uvby-szűrőkön keresztül. A méréshez a Szegedi Csillagvizsgáló 40 cm-es Cassegrain-távcsövét és egycsatornás SSP-5A fotoelektromos fotométert használtunk. Differenciális fotometriát végeztünk, összehasonlítóként a HD16647 (V = 625) jelű csillagot használtuk. 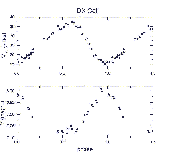Sajnos az ég ezen a napon sem volt teljesen alkalmas fotometriai mérésekre, ezért a fénygörbéknek viszonylag nagy a szórásuk (kb. ±0.02 mag.). A heliocentrikus radiálissebesség-görbe és a fénygörbe az 18. ábrán látható. Az ábrán jól látszik, hogy a radiálissebesség-görbe szinte pontosan a tükörképe a fénygörbének, ami a radiális módban történő pulzáció egyik jele. Szinte a sugárirányú rezgésre utal mind a fény-, mind a radiális sebesség görbe viszonylag nagy amplitúdója.
 

 M_V=1.78±0.24 mag.
 M_bol=1.63±0.24 mag.
 L=17,8±4 L_¤
 [Fe/H]=-0,05±0,2
 <T_eff>=7250±200 K
 <log g>=3,6±0,2 dex
 <R_*>=2,7±0,5 R_¤
 M_*=1,1±0,6 M_¤

Mindezen értékek nem esnek bele az RR Lyrae csillagokra jellemző értéktartományokba, viszont jellemzőek egy tipikus d Scuti csillagra. Végső következtetésünk - a fizikai paraméterekre alapozva -, hogy a DX Ceti egy nagy amplitúdójú, monoperiodikus d Scuti csillag.
   A pulzáció módusa szintén egy fontos kérdés. A vizuális fénygörbe és a radiális sebesség-görbe viszonylag nagy amplitúdója radiális pulzációra utal. A pulzációs konstans számolt értéke Q=0,029±0,012. Az elméleti pulzációs modellek szerint (pl. Petersen & Jørgensen 1972, Milligan & Carson 1992) mind az alap, mind az első felhangbeli pulzációval jól egyeztethetőek a fizikai paraméterek megfigyelt értékei. A DX Ceti log T_eff-log g és log T_eff-log L/L_¤ diagramokon elfoglalt helyzete az M=1,8-2 M_¤ tömegekhez tartozó evolúciós útvonalakhoz nagyon közel esik (Breger & Pamyatnykh 1998). Mindezeken túl még érdekes eredmény az is, hogy Breger & Pamyatnykh (1998) d Scuti csillagok periódusváltozásával kapcsolatos evolúciós számításai alapján a DX Cet-hez hasonló paraméterű változók periódusa igen stabil, jó egyezésben a vonatkozó megfigyelésekkel.