<<vissza    tartalom    tovább>>
 

III. AZ EXTINKCIÓS ÉS STANDARD TRANSZFORMÁCIÓS EGYÜTTHATÓK MEGHATÁROZÁSA

III.1. Az UBV-rendszer együtthatói

   Mint fent említettem, az extinkciós és transzformációs együtthatók kedvező esetben csak hosszú idő alatt változnak meg kimutathatóan. Éppen ezért a Johnson-rendszer tarnszformációs együtthatóit nem határoztam meg újra méréseimhez, hanem  Kiss (1995) értékekeivel számoltam. Az extinciós együtthatók:
 
 

Ext. együtth.
érték + hiba
k'V
0,43 ± 0,008
k'BV
0,26 ± 0,007
k'UB
0,38 ± 0,010
 3. táblázat.
 

   A transzformációs együtthatók és zérusponti állandók:
 
 

e
-0,059 ± 0,004
zV
14,45 ± 0,005
m
1,189 ± 0,002
zBV
1,361 ± 0,002
y
0,97 ± 0,006
zUB
 -0,99 ± 0,006
 4. táblázat.

III.2. A Strömgren-rendszer együtthatói

   A fotométer uvby szűrősorozatát szeptember elején megtisztították, ami által javult az áteresztőképességük, viszont az extinkciós és standard transzformációs együtthatókat újra meg kellett határozni.
   1998. október 14-én 23 csillagot mértem, forrásként Crawford & Barnes (1970) standard csillagokat tartalmazó listáját használtam. A Hipparcos katalógus átnézése után hat csillagról kiderült, hogy kis amplitúdójú változócsillag, ezért standardnak nem alkalmas, három csillag adatait pedig azért kellet kihagynom a számításokból, mert túlságosan északon (vagyis a város zavaró fényeitől szennyezett égterületen) helyezkedtek el a mérés idején. A rostáláson átjutott csillagok adatait az 5. táblázat tartalmazza:
 
Csillag
Színképtípus
V
b-y
m1
c1
q Cyg
F4V
4.5
0.261
0.158
0.506
30 Cyg
A3III
4.8
0.068
0.150
1.310
a Del
B9V
3.8
-0.019
0.125
0.893
h Peg
G8II?+F?
3.0
0.535
0.296
0.499
a Peg
B9.5III
2.5
-0.012
0.130
1.128
i Peg
F5V
3.8
0.296
0.159
0.446
p2 Peg
F5II-III
4.3
0.304
0.177
0.778
u And
F8V
4.1
0.344
0.179
0.409
q And
A2V
4.6
0.026
0.180
1.050
b Tri
A5III
3.0
0.071
0.191
1.065
d Tri
G0V
4.9
0.386
0.191
0.254
b Ari
A5V
2.6
0.064
0.211
0.983
i Per
G0V
4.0
0.376
0.201
0.376
10 Tri
A2V
5.0
0.011
0.161
1.145

 5. táblázat.
 
   Következő lépésként a (26)-(29) egyenleteket beírjuk a (30)-(33) összefüggésekbe. Ekkor egy négy egyenletből álló, 14 független paramétert tartalmazó egyenletrendszert kapunk. A standard csillagok mért instrumentális magnitúdójához kell hozzáilleszteni az egyenletrendszert. P. Sherrod NLREG nevű programját használtam a probléma megoldásához. A program a legkisebb négyzetek módszerét alkalmazza és statisztikia analízist is végez. Az eredmények 6. és 7. táblázatban láthatók.
 
Extink. együtth.
érték + hiba 
K
0,281 ± 0,186 
K1
0,102 ± 0,072
K2
0,172 ± 0,183 
K3
0,427 ± 0,304 
 6. táblázat.
 
 
 
A
(12,02 ± 0,21)
F
0,72 ± 0,32
B
0,18 ± 0,06
G
(0,47 ± 0,37)
C
1,55 ± 0,10
H
0,94 ± 0,01 
D
(1,37 ± 0,05)
I
-0,48 ± 0,17 
E
(-0,35 ± 0,28)
J
-0,13 ± 0,13 
 7. táblázat.

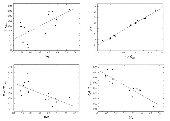
   Zárójelben a zérusponti tagok szerepelnek, amik a differenciális fotometria alkalmazásával nem jutnak szerephez. Amúgy ezek a tagok éjszakáról-éjszakára változnak, értékük csak méréssel határozható meg. Az úgynevezett „all-sky" fotometria esetén minden este standard csillagokat is kellene mérni, ami a változó mérésére fordítható időt jelentősen csökkenti. A 4. ábrán bemutatom a fent említett linearizált összefüggések grafikonjait.
   A D, F, H együtthatók elméletileg 0-hoz, a B, I, J együtthatók elméletileg 1-hez közeli értékűek. Az én általam kapott értékek az elméleti értékektől való viszonylag nagy eltérése azt mutatja, hogy a szűrősorozat, a fotométer és az asztroklíma együttes hatásai miatt közel sem tökéletesen valósul meg az uvby-rendszer.
 

4. ábra. A Strömgren standard transzformációs együtthatók meghatározása


 
<<vissza    tartalom    tovább>>