<<vissza
tartalom tovább>>
II. A MÉRÉSI TECHNIKÁK BEMUTATÁSA
Fotometriai méréseinkhez a Szegedi Csillagvizsgáló
40 cm-es Cassegrain-távcsövét, és a távcsőhöz
csatlakoztatott, Optec SSP-5A típusú egycsatornás
fotométert használtuk.
Az SSP-5A impulzusszámláló fotométer,
vagyis kimenetén a detektorba érkező fotonszámmal
arányos elektronszám (impulzusszám) mérhető.
Ezen adatokat egy IBM-kompatibilis számítógép
a soros portján keresztül olvassa be és rögzíti.
A fotométerhez tartozik egy, a számítógép
által vezérelt szűrőváltó, amelyben
Johnson-féle UBV és Strömgren-féle uvby
szűrősorozatok találhatók.
Minden esetben differenciális fotometriai mérést
alkalmaztunk, vagyis a változócsillag fényességét
egy másik, megfelelően kiválasztott, állandó
fényességűnek feltételezett csillagéhoz
viszonyítottuk (az összehasonlító stabilitását
a Hipparcos asztrometriai műhold 4 éven keresztül végzett
folyamatos fényességmérései igazolták
- ESA, 1997).
A spektroszkópiai mérések a torontói
David Dunlap Observatory (DDO) 1,88 m-es távcsövével
készültek. 1998 októberére 5 órányi
távcsőidőt (ez a V2109 Cyg periódusának
hossza) pályáztunk meg, melyet végül is október
19/20., ill. 21/22. éjszakáján kaptunk meg. Észleléseinket
november 17/18-án folytattuk, három órányi
spektroszkópiával (DX Cet). A spektrális bontóelem
egy reflexiós ráccsal működő spektrográf
a távcső Cassegrain-fókuszában, míg a
színképet egy 1024x1024-es CCD kamera rögzíti.
A műszereket a DDO személyzete kezelte (elsősorban J.R.
Thomson, az obszervatórium legtapasztaltabb éjszakai segítője),
a felvételeket pedig az obszervatórium számítógépéről
a hálózaton keresztül töltöttük le.
II.1. Röviden a csillagászati fotometriáról
Az első, feljegyzett csillagkatalógust az
i.e. II. században élt görög Hipparkhosz készítette.
Katalógusában a csillagok fényességéhez
számszerű értéket rendelt. Rendszere szerint
a 12 legfényesebb csillag 1. rendű, azaz 1 magnitúdós,
a leghalványabb, még éppen látható csillagok
pedig 6 magnitúdósak. A köztes fényességű
csillagokat pedig az 1 és 6 magnitúdó közé
eső osztályokba sorolta.
A magnitúdóskálát az 1850-es
évek végén helyezték fizikai alapokra. Jelenleg
is a Norman Pogson által javasolt rendszer érvényes,
amely szerint
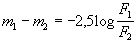 ,
(1)
,
(1)
ahol m1 és m2 a két csillag látszó
fényessége magnitúdóban, F1
és F2 pedig a detektált fluxusuk. A logaritmikus
jelleget a látás fiziológiai sajátosságai
indokolják.
Az abszolút magnitúdó számértéke
azt mutatja meg, hogy hány magnitúdósnak észlelnénk
a csillagot, ha az tőlünk 10 parszek (kb. 32,6 fényév)
távolságban lenne. Jelölése: M. Az összefüggés
a csillag látszólagos m és abszolút M magnitúdója
között a következő:
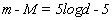 ,
(2)
,
(2)
ahol d a csillag távolsága parszekben.
További összefüggések a magnitúdóskálán
alapuló fotometriára (részletesen l. Henden &
Kaitchuk, 1990, vagy Budding, 1993):
- (1) természetesen hullámhosszfüggő
mennyiség. A referenciacsillagot 0 magnitúdósnak véve
(1)-ből a következőt kapjuk:
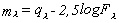 ,
(3)
,
(3)
ahol ql egy
állandó. Felmerülő probléma: (3)-ban a
Földön megfigyelt fluxus szerepel, ami azonban különbözik
a valódi fluxustól a légkör elnyelése,
a fényszóródás és a műszer torzító
hatásaitól függően. A mért fluxus, Fl
az alábbi egyenlet szerint függ a valóditól (F*l):
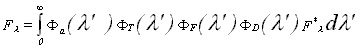 ,
(4)
,
(4)
ahol
FA(l')
= a földi légkör áteresztési függvénye
FT(l')
= a távcső áteresztése
FF(l')
= a szűrő áteresztése
FD(l')
= a detektor hatásfoka (<1);
- a gyakorlatban nem a fluxust mérjük, hanem valamilyen
fluxussal arányos mennyiséget, esetünkben az impulzuszámláló
fotométerrel a beütésszámot (Nl).
Feltételezzük, hogy
 ,
(5)
,
(5)
ami felhasználásával (2) átírható
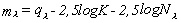 (6)
(6)
alakba, tehát
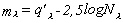 .
(7)
.
(7)
Ezzel bevezettük az instrumentális magnitúdó
(ml) fogalmát. q'l
az instrumentális zéruspont.
- A csillag színindexe két különböző
hullámhossztartományban mért fényességérték
különbsége:
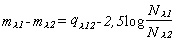 .
(8)
.
(8)
- a légköri hatásokat egy egyszerű korrekcióval
vesszük figyelembe:
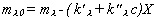 ,
(9)
,
(9)
ahol k'l és k''l
az első- ill. másodrendű extinkciós
együttható, c a mért színindex, X
pedig egy levegőtömegnek nevezett mennyiség. Jó
közelítéssel
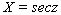 ,
(10)
,
(10)
ahol z a csillag zenittávolsága (=90° - horizont
feletti szögmagasság). 0,1%-os pontossággal X:
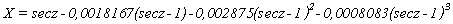 ; (11)
; (11)
- a fentieket figyelembe véve egy tetszőleges színindex
extinkcióra korrigált értéke:
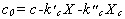 .
(12)
.
(12)
Az extinkciós együtthatók meghatározott
csillagok megfigyelésével meghatározhatók.
Az ismertetett összefüggések változtatás
nélkül átvihetők a változócsillag
és az összehasonlító közötti fénnyességkülönbségre
is. Ekkor az egyenletekben nem a változócsillag fényessége,
hanem egy másik csillaghoz viszonyított különbsége
szerepel. Ez természetesen érvényes a színindexekre
is.
A másodrendű extinkciós korrekciót
általában elhagyjuk, mert a változó és
az összehasonlító csillag elég közel van
egymáshoz, hogy a magasabb rendű Xc kifejezést
elhanyagolhassuk; k''c pedig az elsőrendű
együtthatóhoz képest kicsi. A tapasztalat azt mutatja,
hogy 1°-on belül lévő összehasonlító
esetén az az extinkciós korrekció kb. 0,001-0,006
magnitúdó, ami jóval kisebb, mint a műszerek
és a légköri szcintilláció által
bevitt szórás. Századmagnitúdónál
nagyobb pontosságú mérésre csak a városoktól
(vagyis zavaró fényektől) távoli, nagy tengerszint
feletti magasságon található obszervatóriumokban
nyílik lehetőség.
II.2. Nemzetközi fotometriai rendszerek
Az 1950-es években, a fotoelektromos fotometria
terjedésével felmerült az igény egy egységes
fotometriai rendszerre, ami segítségével a különböző
a asztroklímájú helyeken, különböző
detektorokkal, eltérő méretű távcsövekkel
észlelő csillagászok mérési eredményei
összevethetővé válnak. A detektor típusa,
a szűrősorozat, a használt távcső és
a korrekciós eljárás alkotja együttesen a természetes
fotometriai rendszert. Tehát minden megfigyelű saját
természetes rendszerrel rendelkezik. A standard rendszereket
az egyes szerzők úgy definiálják, hogy a saját
természetes rendszerükkel megmérik, és rögzítik
egy sor típuscsillag standard fényességét és
színindexét. Ezen csillagok a standardcsillagok. Más
észlelők ezen standard csillagok mérésével,
a standard korrekciós eljárás ismeretében meg
tudják határozni, hogy méréseiket mi módon
lehet áttranszformálni a standard rendszerbe. Ez konkrétan
úgy történik, hogy az észlelő megméri
a standard csillagokat, és a kapott instrumentális magnitúdókból
transzformációs egyenleteket old meg.
Az alábbiakban a két legjobban elterjedt,
általunk is használt standard rendszert ismertetem.
II.2.1. A Johnson-féle szélessávú UBV-rendszer
A legszélesebb körben elterjedt rendszer a
Johnson-féle UBV. Ezt később kiterjesztették
az infravörös tartományra is az R, I, J, K, L, M szűrőkkel.
A rendszert három szélessávú szűrő
valósítja meg (U = ultraviolet; B = blue; V = visual), áteresztési
függvényeik a 2. ábrán (GCPD,
1997) láthatók, részletes adataikat az 1. táblázat
tartalmazza (Budding, 1993).
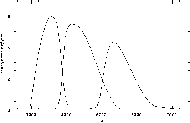 2. ábra. Az UBV rendszer szűrőfüggvényei
2. ábra. Az UBV rendszer szűrőfüggvényei
|
Szűrő
|
Központi hullámhossz (nm)
|
Sávszélesség (nm)
|
|
U
|
350
|
70
|
|
B
|
440
|
100
|
|
V
|
550
|
90
|
1. táblázat.
A rendszer transzformációs egyenletei
a következőképpen állnak elő (Henden &
Kaitchuk, 1982):
- Legyen NU, NB, NV a
csillagról a három szűrőn keersztül mért
beütésszám. Ekkor az instrumentális magnitúdók:
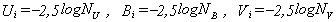 ,
(13a,b,c)
,
(13a,b,c)
a színindexek:
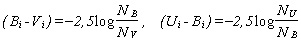 (14a,b)
(14a,b)
- az extinkciós korrekció (9)-nek megfelelően:
Fontos megjegyezni, hogy a Johnson-rendszerben k''UB
definíció szerint zérus, valamint a mérések
során a B-V transzformációnál is elhanyagoltuk
a másodrendű korrekciót.
- Végezetül a standard rendszerbe való átszámítást
egy lineáris transzformációval végezzük
el:
ahol e, m, y transzformációs
együtthatók, míg zV,
zBV, zUB
zérusponti állandók. Ez a hat állandó
szintén standard csillagok megfigyelésével határozható
meg.
Differenciális fotometriánál annyi a
változás, hogy az instrumentális magnitúdókülönbségekben
a beütésszámok hányadosa szerepel, míg
az extinkciós korrekciónál X helyébe
az Xvar-Xcomp levegőtömeg-külünbséget
írjuk. Ez utóbbi egymáshoz közel lévő
csillagok esetében igen kicsi érték, ami az extinkciós
korrekció fontosságát erősen csökkenti.
A transzformációs egyenletek differenciális fotometria
esetén:
A differenciális fotometria legnagyobb előnye
egyértelműen látszik, mert a transzformációs
egyeneletekből kieső zérusponti állandók
éjszakáról-éjszakára jelentősen
változhatnak, míg a szín-tagok együthatói
csak hónapok alatt változnak meg kimutathatóan. Így
nem kell minden éjszaka újra és újra standard
csillagokat is mérni.
A Johnson-rendszer egyik legnagyobb problémája,
hogy az U szűrő átviteli függvényének
rövidebb hullámhosszú oldalát nem az átviteli
függvény, hanem a légkör e tartománybeli
elnyelése határozza meg. Ez pedig jelentősen eltér
a Föld különböző pontjain, és szezonális
változást is mutat. Ennek eredményeképpen az
U méréseket (ill. az U-B színindexet) terheli a legnagyobb
hiba.
A rendszer felállítása után
többféle kalibrációt végeztek el a színindexekre.
Ezek közül az egyik legfontosabb a B-V index hőmérséklettel
való arányossága. Az asztrofizikában használt
színhőmérsékletet éppen ez az index szolgáltatja.
Például egy változócsillag B-V indexének
változása első közelítésben a csillag
fotoszférájának hőmérsékletváltozását
adja meg.
II.2.2. A Strömgren-féle négyszín-rendszer
A másik, gyakran használt fotometriai rendszer
a 60-as években megalkotott Strömgren-féle uvby.
Ezt a rendszer közepes sávszélességű szűrők
határozzák meg, elnevezéseik magukért beszélnek
(u = ultraviolet, v = violet, b = blue, y = yellow). A szűrőfüggvények
a 3. ábráról olvashatók le; adataikat számszerűen
a 2. táblázat tartalmazza (GCPD, 1997; Budding, 1993.). Ez
(illetve a kibővített uvbyb)
az első fotometriai rendszer, amit már eleve úgy alkottak
meg, hogy bizonyos színképtípusú csillagok
egyes fizikai paramétereit (Teff, felszíni gravitációs
gyorsulás, fémtartalom) közvetlenül meg lehessen
határozni vele.
|
Szűrő
|
Központi hullámhossz (nm)
|
Sávszélesség (nm)
|
|
u
|
347
|
38
|
|
v
|
411
|
20
|
|
b
|
467
|
10
|
|
y
|
546
|
20
|
2. táblázat.
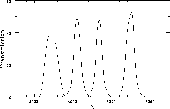 3. ábra. Az uvby szűrők transzmissziós
görbéi
3. ábra. Az uvby szűrők transzmissziós
görbéi
Az uvby rendszernek számos előnye van az UBV-vel
szemben. Például a szűrőfüggvények
egyértelműen meghatározottak, áteresztésük
nem függ a légkörtől, színindexeik több
fizikai paraméterre lettek kalibrálva, ráadásul,
a rendszer speciális definiálásából
következően a légköri extinkció csupán
elsőrendű korrekció. Az újabb vizsgálatok
szerint a b-y színindex megbízhatóbb hőmérsékleti
indikátor, mint a B-V. A Strömgren rendszer hátránya
viszont a kisebb sávszélességéből adódó
kisebb áteresztőképesség. Tapasztalat szerint
UBV szűrőkkel 1,5-2 magnitúdóval fényesebb
csillagok mérhetők, mint uvby-nal.
A Strömgren rendszer kissé eltérő
színindexeket használ. Az y fényességből
a transzformációs egyenletek (l. alább) közvetlenül
V fényességet adnak. Az effektív hőmérsékletre
kalibrált b-y színindex értelemszerűen a b és
y fényességek különbsége, majdnem analóg
a B-V színindexszel. Az
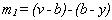 (24)
(24)
színindex („fémindex") a blanketing-effektus mértékét
jellemzi. Bizonyos színképtípusú csillagokra
erős korreláció mutatkozik a csillag relatív
fémtartalma és a színindex értéke között.
A
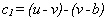 (25)
(25)
színindex a csillag színképében fellépő
Balmer-ugrás erősségét méri. (Részletekre
vonatkozóan l. Budding, 1992, vagy Henden & Kaitchuk, 1990)
Kisebb felszíni hőmérsékletű csillagok
esetében c1 értékéből a felszíni
gravitációs gyorsulás nagyságára, forró
csillagok esetén pedig a fotoszféra hőmérsékletére
lehet következtetni. (Napiwotzki et. al., 1992.)
A rendszer transzformációs egyenletei kissé
különböznek a Johnson-rendszerétől. A szokásos
jelölések (l. Crawford & Barnes, 1970):
Az „i" indexes mennyiségek a beütésszámokból
származó instrumentális magnitúdókat
jelentik, K, K1, K2, K3 pedig extinkciós
együtthatók, standard csillagok mérésével
maghatározhatók.
Mivel a Strömgren rendszer színindexei kevert
jellegűek, azaz színindexek különbségeiből
állnak elő, a standard transzformáció más
alkú. Mivel az y szűrő központi hullámhossza
megegyezik a Johnson V-ével, a transzformációs egyenletek
egyből Johnson-féle V fényességet adnak, tehát
standard „y" fényesség tulajdonképpen nem létezik.
Az egyenletek:
A színindexek kevert jellege - illetve (30)-ban a v
szűrő sajátossága - hozza be az extra (b-y)-tól
függő (színfüggő) tagot. Az A, B, C, D,
E, F, G, H, I, J együtthatók szintén standard csillagok
mérésével állapíthatók meg.
II.3. Spektroszkópia
Az asztrofizika egyik legeredményesebb vizsgálati
módszere a színképelemzés (l. Vinkó
et al., 1997). A csillagspektrum vonalainak elemzésével információkat
nyerhetünk a csillag légkörének kémiai összetételéről,
illetve a vonalak keletkezési helyén uralkodó fizikai
körülményekről (pl. gravitációs gyorsulás,
hőmérséklet, elektromos és mágneses térerősség,
helyi mozgásviszonyok). Ezenkívül a csillagok típusfelosztása
is a spektroszkópián alapul.
A csillagspektrumokból az egyik legkönnyebben
kinyerhető információ a radiális sebesség,
amit kétféle módon határozhatunk meg:
- a színképvonalak azonosítása után
az egyedi vonalak Doppler-eltolódásának mérésével,
vagy
- ismert, standard sebességcsillagok spektrumával
való keresztkorreláció segítségével.
Az utóbbi módszer nagy előnye, hogy nem
egyedi vonalakkal kell dolgozni, hanem gondosan kiválasztott hullámhossz-tartományokkal,
amelyek még viszonylag kis jel/zaj viszony esetén is pontos
sebességeket adnak. Célszerű a vizsgált csillagéhoz
hasonló színképtípusú sebesség-standardot
használni, így ugyanis biztosíthatjuk, hogy ugyanazon
elemek vonalai fognak dominálni a korrelált spektrumokban.
Az általunk feldolgozott színképek a DDO
1,88 m-es távcsövének Cassegrain-spektrográfjával
készültek. Az alkalmazott detektor egy 1024x1024-es Thomson
CCD chip volt; a diszperzió 10,5 Å/mm, a felbontás
l/Dl»11000 a Ha
vonalnál. A spektrumok 200 Å széles tartományt
fedtek le, közepes hullámhosszuk 6600 Å. Itt található
a hidrogén Balmer-sorozatának a
vonala, ill. kb. egy tucatnyi fotoszférikus fémvonal. Pontos
hullámhossz-kalibrációra Fe-Ar spektrállámpáról
készült színképfelvételeket használtunk.
A csillagspektrumok expozíciós ideje 3-5 perc volt, a programcsillagok
periódusától függően. A hullámhossz-kalibrációnál
ügyeltünk a Fe-Ar összehasonlító spektrumok
közötti lineáris interpolációra, ugyanis
a távcső elfordulásával fellépő
mechanikus torzulások kihathatnak a spektrográf leképezésére
is (tapasztalataink szerint közel 1 km/s-os zajt okoz ennek elhanyagolása).
A spektrumokat az IRAF képredukáló
programcsomaggal mértük ki. A digitális képfeldolgozás
legfontosabb lépéseit (bias és flatkorrekció)
az alap rutinokkal végeztük el, míg a spektrumok CCD
képekből történő extrakciója a noao.imred.kpnoslit
csomag vonatkozó programjaival (ún. taskokkal) történt.
A radiális sebesség-változás keresztkorrelációs
meghatározására a noao.rv.fxcor taskot alkalmaztuk.
<<vissza
tartalom tovább>>