Next: A folyadékváltozók kifejezése a Up: Relativisztikus csillagmodellek Previous: Az Oppenheimer-Volkoff-egyenlet
Adott barotropikus állapotegyenlet feltevése mellett explicit
relativisztikus csillagmegoldások vezethetők le. Ezek közül legegyszerűbb a
belső Schwarzschild-megoldás, amelyet állandó
![]() energiasűrűség feltevése mellett kapunk. Metrikus függvényei:
energiasűrűség feltevése mellett kapunk. Metrikus függvényei:
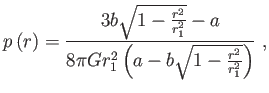 |
(5.19) |