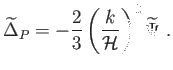A mértékinvariáns
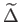 sűrűségperturbáció helyett célszerű
bevezetni a
sűrűségperturbáció helyett célszerű
bevezetni a
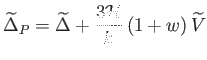 |
(6.100) |
kombinációt. Az Einstein-egyenletekből megmutatható, hogy
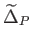 -t előjeltől eltekintve ugyanolyan Poisson-egyenlet kapcsolja a
-t előjeltől eltekintve ugyanolyan Poisson-egyenlet kapcsolja a
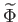 Bardeen-potenciálhoz, mint a newtoni folyadékok mechanikájában a
Bardeen-potenciálhoz, mint a newtoni folyadékok mechanikájában a 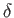 relatatív sűrűségperturbációt a newtoni gravitációs potenciálhoz. Anizotrop nyomásmentes közegben
relatatív sűrűségperturbációt a newtoni gravitációs potenciálhoz. Anizotrop nyomásmentes közegben
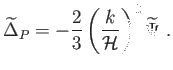 |
(6.101) |
A
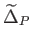 definíciójából látható, hogy kis hullámhosszú
(szub-Hubble-) fluktuációkra:
definíciójából látható, hogy kis hullámhosszú
(szub-Hubble-) fluktuációkra:
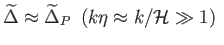 |
(6.102) |
adódik.
A sugárzásra, illetve porra (6.91)-ből
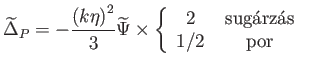 |
(6.103) |
adódik. Por esetén (6.83) és (6.103) összefüggésekből
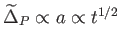 , akárcsak a newtoni mechanikában a
, akárcsak a newtoni mechanikában a 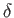 relatív sűrűség-perturbációra. A Fourier-transzformált sűrűség-perturbáció időben növekvő amplitúdója a háromdimenziós térben periodikus
sűrűsödéseket-ritkulásokat jelent, amelyek a struktúra képződéséhez vezetnek.
relatív sűrűség-perturbációra. A Fourier-transzformált sűrűség-perturbáció időben növekvő amplitúdója a háromdimenziós térben periodikus
sűrűsödéseket-ritkulásokat jelent, amelyek a struktúra képződéséhez vezetnek.
Szeged
2013-05-01
![]() sűrűségperturbáció helyett célszerű
bevezetni a
sűrűségperturbáció helyett célszerű
bevezetni a