Next: Hosszú és rövid hullámhosszú Up: Perturbációk a sugárzás- és Previous: Sűrűségperturbációk
Sugárzás esetén (6.95) kifejezés (
![]() ) adja a
Bardeen-potenciált és (6.103)
) adja a
Bardeen-potenciált és (6.103)
![]() -t. Ezek
felhasználásával (6.89) ad egyenletet a
-t. Ezek
felhasználásával (6.89) ad egyenletet a
![]() sebesség
perturbációra, ezek után (6.100)-ból származtatható
sebesség
perturbációra, ezek után (6.100)-ból származtatható
![]() .
.
Szuper-Hubble-skálán
![]() -ban vezető rendben [26]:
-ban vezető rendben [26]:
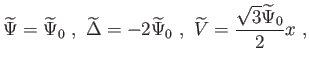 |
(6.104) |
| (6.105) |
Szub-Hubble-skálán (![]() ) konstans amplitúdójú
) konstans amplitúdójú
![]() frekvenciával oszcilláló megoldásokat találunk [26]:
frekvenciával oszcilláló megoldásokat találunk [26]:
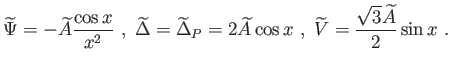 |
(6.106) |
A fentiekből azt valószínűsíthetjük, hogy nagy skálán a perturbációk
befagynak'', vagyis konstansok. Adott hullámhossz esetén a
![]() Hubble skála idővel nő. Amikor a perturbáció hullámhossza a Hubble-skála alá ér, a sűrűségperturbációk növekedni
kezdenek a gravitáció hatására. Azonban a sugárzás nyomása ellenáll a
gravitációs erőnek'', így a folyadék fluktuációi konstans amplitúdóval oszcillálni kezdenek (akusztikus oszcillációk).
Hubble skála idővel nő. Amikor a perturbáció hullámhossza a Hubble-skála alá ér, a sűrűségperturbációk növekedni
kezdenek a gravitáció hatására. Azonban a sugárzás nyomása ellenáll a
gravitációs erőnek'', így a folyadék fluktuációi konstans amplitúdóval oszcillálni kezdenek (akusztikus oszcillációk).
Szeged 2013-05-01