Az anizotrop nyomásperturbációk elhanyagolása után a (6.87)
Einstein-egyenlet a Bardeen-potenciálok
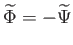 kapcsolatát adja. A
kapcsolatát adja. A
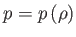 alakú állapotegyenlet arra
vezet, hogy nincs az anyagnak belső entrópiaperturbációja, így
alakú állapotegyenlet arra
vezet, hogy nincs az anyagnak belső entrópiaperturbációja, így  .
A perturbációk fejlődési egyenleteiből a
.
A perturbációk fejlődési egyenleteiből a
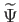 Bardeen-potenciálra az alábbi homogén, csillapított hullámegyenlet
származtatható [26]:
Bardeen-potenciálra az alábbi homogén, csillapított hullámegyenlet
származtatható [26]:
![$\displaystyle
\frac{d^{2}\widetilde{\Psi }}{d\eta ^{2}}+3\left(
1+c_{s}^{2}\rig...
...c_{s}^{2}-w\right)
\mathcal{H}^{2}+c_{s}^{2}k^{2}\right] \widetilde{\Psi
} =0 .$](img1403.png) |
(6.90) |
Továbbá, ha 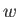 konstans, érvényes (6.83), így
konstans, érvényes (6.83), így
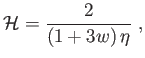 |
(6.91) |
és
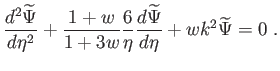 |
(6.92) |
Az Einstein-egyenletek megoldását két határesetben tárgyaljuk. A
határesetek
az úgynevezett szuper- és szub-Hubble skálákhoz kötődnek.
Szuper-Hubble-skálákon a
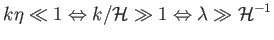 |
(6.93) |
relációk teljesülését értjük. Vagyis olyan perturbációkat tekintünk,
amelyek
hullámhossza lényegesen meghaladja a konformis Hubble-paraméter
reciprokát.
Szub-Hubble-skála alatt a fenti relációk ellentettjeit értjük:
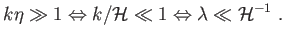 |
(6.94) |
Ekkor olyan perturbációkat tekintünk, amelyek hullámhossza
lényegesen kisebb
a konformis Hubble-paraméter reciprokánál.
A (6.92) egyenletnek van egzakt
partikuláris megoldása, amely 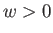 esetben [26]:
esetben [26]:
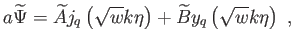 |
(6.95) |
ahol 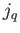 és
és 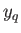 jelölik a
jelölik a 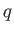 -adik (
-adik (
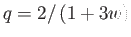 )
rendű
szférikus Bessel-függvényeket. Amikor
)
rendű
szférikus Bessel-függvényeket. Amikor
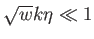 (szuper-Hubble skála),
(szuper-Hubble skála),
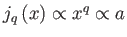 és
és
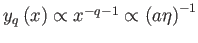 . Ezért
és (6.91) miatt
. Ezért
és (6.91) miatt
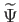 mennyiség
mennyiség
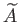 -módusa
konstans, míg a
-módusa
konstans, míg a
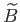 -módus
csökkenő
-módus
csökkenő
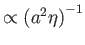 .
Eredetileg összemérhető amplitúdójú módusok esetén is a
.
Eredetileg összemérhető amplitúdójú módusok esetén is a
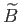 -módus
csökkenése gyors, így mindig elhanyagolható. Ha
-módus
csökkenése gyors, így mindig elhanyagolható. Ha
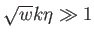 (szub-Hubble-skála) a megoldás
(szub-Hubble-skála) a megoldás 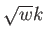 frekvenciával
oszcillál, amplitúdója
frekvenciával
oszcillál, amplitúdója
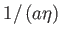 szerint csökken:
szerint csökken:
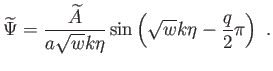 |
(6.96) |
A 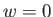 esetben
(6.92) megoldása [26]:
esetben
(6.92) megoldása [26]:
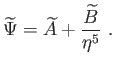 |
(6.97) |
Mivel a
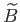 -módus
csökkenő, a gravitációs potenciál perturbációja időfüggetlen a
pordominált korszakban.6.11 Tehát a pordominált,
lecsatolódás utáni Univerzumban a
perturbációknak mindkét skálán létezik konstans járuléka.
-módus
csökkenő, a gravitációs potenciál perturbációja időfüggetlen a
pordominált korszakban.6.11 Tehát a pordominált,
lecsatolódás utáni Univerzumban a
perturbációknak mindkét skálán létezik konstans járuléka.
A széles körben elfogadott inflációs modellek szerint a
sugárzásdominált időszakra a kezdeti
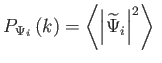 |
(6.98) |
spektrum a következő egyenletet teljesíti:
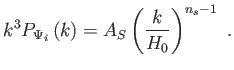 |
(6.99) |
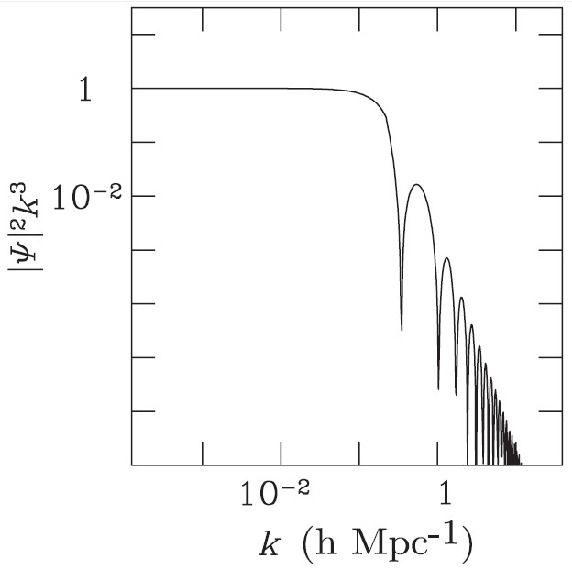
6.9. Ábra:
A 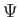 Bardeen-potenciál
Bardeen-potenciál
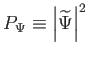 spektrumából képezett
spektrumából képezett
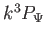 a hullámszám függvényében az Univerzum késői, pordominált
korszakában [26]. (Az ábrán
a hullámszám függvényében az Univerzum késői, pordominált
korszakában [26]. (Az ábrán
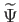 -t
-t 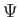 jelöli.)
jelöli.)
|
|
Az 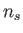 spektrális index
spektrális index 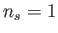 értékére a
értékére a
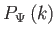 spektrumot a 6.9 ábra mutatja. Ez egy
olyan sík
Friedmann-univerzum késői pordominált korszakára vonatkozik,
amelynek a sugárzásdominált kezdeti korszakában a spektrum (6.99) volt.
spektrumot a 6.9 ábra mutatja. Ez egy
olyan sík
Friedmann-univerzum késői pordominált korszakára vonatkozik,
amelynek a sugárzásdominált kezdeti korszakában a spektrum (6.99) volt.
Szeged
2013-05-01
![]() kapcsolatát adja. A
kapcsolatát adja. A
![]() alakú állapotegyenlet arra
vezet, hogy nincs az anyagnak belső entrópiaperturbációja, így
alakú állapotegyenlet arra
vezet, hogy nincs az anyagnak belső entrópiaperturbációja, így ![]() .
A perturbációk fejlődési egyenleteiből a
.
A perturbációk fejlődési egyenleteiből a
![]() Bardeen-potenciálra az alábbi homogén, csillapított hullámegyenlet
származtatható [26]:
Bardeen-potenciálra az alábbi homogén, csillapított hullámegyenlet
származtatható [26]:![]() esetben [26]:
esetben [26]: