Next: Perturbációk a sugárzás- és Up: Kozmológiai perturbációszámítás Previous: Skalárperturbációk
A felvázolt mértékinvariáns mennyiségeket Bardeen vezette be elsőként [25]. E mennyiségeket alkalmazó lineáris perturbációszámítást
Bardeen-formalizmusnak nevezik. A ![]() ,
, ![]() Bardeen-potenciálok és a
Bardeen-potenciálok és a ![]() ,
, ![]() ,
, ![]() ,
, ![]() kozmikus folyadék perturbációk fejlődését
az Einstein-egyenletek adják meg. Közönséges differenciálegyenteket nyerünk,
ha a térbeli függést harmonikusok szerinti kifejtéssel leválasztjuk az időbeli függéstől. A harmonikusok a
kozmikus folyadék perturbációk fejlődését
az Einstein-egyenletek adják meg. Közönséges differenciálegyenteket nyerünk,
ha a térbeli függést harmonikusok szerinti kifejtéssel leválasztjuk az időbeli függéstől. A harmonikusok a
![]() Laplace-Beltrami-egyenlet megoldásai (
Laplace-Beltrami-egyenlet megoldásai (![]() az állandó görbületű 3-dimenziós tér Laplace-operátora,
az állandó görbületű 3-dimenziós tér Laplace-operátora, ![]() a hullámszám).
a hullámszám).
Az alábbiakban a sík (![]() ) Friedmann-téridő perturbációjával foglalkozunk.
A harmonikusok szerinti kifejtés ekkor a szokásos Fourier-transzformációt
jelenti:
) Friedmann-téridő perturbációjával foglalkozunk.
A harmonikusok szerinti kifejtés ekkor a szokásos Fourier-transzformációt
jelenti:
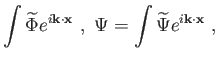 |
|||
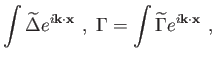 |
|||
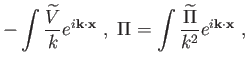 |
(6.79) |
Az egyenletek egyszerűbb alakot öltenek, ha áttérünk az ![]() konformis idő
szerinti6.9deriváltra a
konformis idő
szerinti6.9deriváltra a
| (6.80) |
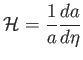 |
(6.81) |
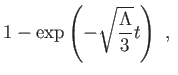 kozmológiai állandó .
kozmológiai állandó . |
(6.82) |
A mértékinvariáns perturbációs változókra az Einstein-egyenletek a következőket adják [26]:6.10
Szeged 2013-05-01