Next: Bardeen-formalizmus Up: Kozmológiai perturbációszámítás Previous: Mértékinvariancia
A struktúraképződés az Univerzumot kitöltő anyag komponensek helytől függő sűrűsödését-ritkulását jelenti. Az energiasűrűség-perturbáció skalár típusú, a
metrika perturbációi pedig két mértékinvariáns mennyiséggel jellemezhetők, a
Bardeen-potenciálokkal. A Bardeen-potenciálok segítségével a téridő
perturbációi mértékinvariánsan tárgyalhatók, azonban a potenciálok interpretációja nehézkes. Könnyen interpretálhatók viszont az ún. newtoni (longitudinális vagy nyírásmentes) mértékben6.8. Newtoni mértékben a ![]() és
és ![]() Bardeen-potenciálok következőképpen jelennek meg a perturbált metrikában:
Bardeen-potenciálok következőképpen jelennek meg a perturbált metrikában:
Az anyagi komponenseket energia-impulzus tenzoruk jellemzi. Feltesszük, hogy
az egyes anyagkomponensek csak gravitációsan hatnak kölcsön és azt, hogy a
perturbált folyadék
![]() állapotegyenlete is
barotropikus. Bevezetjük továbbá a
állapotegyenlete is
barotropikus. Bevezetjük továbbá a
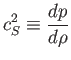 |
(6.78) |
Az univerzumot kitöltő anyagkomponensek együttese alkotja a kozmikus
folyadékot. A kozmikus folyadék energia-impulzus tenzorának skalár típusú
perturbációi négy mennyiséggel paraméterezhetők. Ezek megfelelnek a energiasűrűség, folyadéksebesség, izotrop nyomás és anizotrop nyomástenzor perturbációinak. Ezek közül egyedül az anizotrop nyomástenzor perturbációból képezett ![]() skalár mértékinvariáns. Az energiasűrűség és izotrop nyomásperturbáció
kombinációjából származtatható egy
skalár mértékinvariáns. Az energiasűrűség és izotrop nyomásperturbáció
kombinációjából származtatható egy ![]() mértékinvariáns mennyiség,
amely a perturbációk entrópiafluxusának divergenciájával arányos (lásd pl.
[26] A függelékét). Az izotrop nyomásperturbáció helyett a
mértékinvariáns mennyiség,
amely a perturbációk entrópiafluxusának divergenciájával arányos (lásd pl.
[26] A függelékét). Az izotrop nyomásperturbáció helyett a ![]() -t használják. További mértékinvariáns mennyiségek a metrika perturbációkkal
képezett kombinációkból származtathatók. A
-t használják. További mértékinvariáns mennyiségek a metrika perturbációkkal
képezett kombinációkból származtathatók. A ![]() relatív energiasűrűség-perturbáció helyett általában egy
relatív energiasűrűség-perturbáció helyett általában egy ![]() -val jelölt mértékinvariáns
mennyiséget használnak, azonban newtoni mértékben
-val jelölt mértékinvariáns
mennyiséget használnak, azonban newtoni mértékben
![]() . Hasonlóan a
. Hasonlóan a ![]() sebesség-perturbáció helyett egy
sebesség-perturbáció helyett egy ![]() -vel jelölt mértékinvariáns változót vezetnek be, de newtoni mértékben a kettő megegyezik.
-vel jelölt mértékinvariáns változót vezetnek be, de newtoni mértékben a kettő megegyezik.
Szeged 2013-05-01